Построение координатной сетки
Сетку координат строят на листе ватмана формата А-2. Сторона квадрата сетки принимается для масштаба 1:500 равной 100 мм (что составляет 50 м на местности).
Для получения правильного прямоугольника выполняют следующие построения с помощью измерителя и точной металлической линейки:
· через углы листа ватмана проводят диагонали и от их пересечения откладывают равные отрезки, полученные точки соединяют горизонтальными и вертикальными линиями (рис. 2);
· диагонали убирают резинкой и на полученных сторонах прямоугольника откладывают отрезки по 100 мм, т.е. получают координатную сетку в виде квадратов. Сетку проверяют по сторонам и диагоналям каждого квадрата в отдельности, отклонения построенных размеров от заданных не должно превышать 0,2 мм;
· сетку координат оцифровывают так, чтобы все вершины теодолитного хода располагались внутри рамки симметрично, для этого перед разбивкой сетки из ведомости вычисления координат (прил. 4,5) выбирают максимальные и минимальные координаты по оси абсцисс и по оси ординат и, согласно им, разбивают и подписывают сетку числами, кратными 50 метрам.
· изображение сетки следует выполнять тонкими линиями так, чтобы внутренние линии впоследствии легко стирались; пересечение этих линий фиксируют сохраняемыми | Рис.3. Построение координатной сетки
| крестиками со сторонами 6 мм и оформляют на плане зеленой тушью.
Нанесение вершин теодолитного хода по вычисленным координатам на план
Вершины теодолитного хода наносят на план по их вычисленным координатам (см. прил. 3,4 или табл. 2) в масштабе 1:500.
Пример
| Рис.4. Нанесение вершин теодолитногохода
|   Необходимо нанести на план точку 1 с координатами 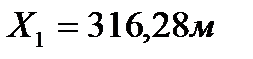 и 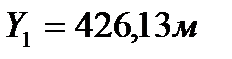 . Сначала выясняют, в каком из квадратов должна лежать эта точка: по направлению X точка должна находится между линиями сетки с абсциссами 300 и 350 м, по направлению Y - между линиями сетки с ординатами 400 и 450 м (рис. 3). От линии с абсциссой 300 по вертикальным сторонам этого квадрата вверх откладывают расстояние 316,28-300 =16,28 м переведенное в масштаб плана (3,25 см) и проводят линию, параллельную линии с абсциссой 300 м. Вдоль нее от вертикальной линии сетки с ординатой 400 м откладывают вправо расстояние 426,13-400=26,13 м переведенное в масштаб плана (5,2 см).
Полученную точку обозначают слабым наколом иглы циркуля-измерителя и обводят окружность диаметром 1,5 мм; внутри этой окружности никакие линии проводить нельзя. Слева записывают номер точки.
Нанесение на план вершин теодолитного хода необходимо проконтролировать. Для контроля измеряют расстояния между нанесенными вершинами: получившиеся на плане длины сторон должны быть равны вычисленным горизонтальным проложениям в ведомости координат (см. прил. Ж, З).
Пример
Горизонтальное проложение стороны 1-2 теодолитного хода равно 108,71 м, следовательно, в масштабе плана расстояние между нанесенными вершинами должно быть 21,7 см.
Допустимое расхождение – 0,2 мм в плане.
Построение контурного плана участка местности по материалам теодолитной съемки
В прил. И приведены абрисы теодолитной съемки сторон и точек съемочного обоснования. На абрисах все измеренные расстояния приведены в м. Для составления плана необходимо, используя данные абриса, откладывать соответствующие расстояния или углы от сторон теодолитного хода методами перпендикуляров, полярных координат, угловых и линейных засечек, створов.
Способ перпендикуляров
Если при съемке применялся способ перпендикуляров, это означает, что измерялось расстояние по стороне теодолитного хода от станции съемочного обоснования до основания перпендикуляра и длина перпендикуляра до снимаемой точки (рис. 5,а). Следовательно, для того, чтобы нанести данную точку на план, необходимо с помощью линейки отложить измеренное расстояние от точки съемочного обоснования, восстановить перпендикуляр и отложить его длину, при этом все измеренные расстояние переводят в масштаб плана, например, 23,57 м на местности соответствуют 4,7 см в плане данного масштаба (рис. 4,б).
| Рис.5. Способ перпендикуляров
| 
Способ полярных координат
С точки теодолитного хода, принимаемой за полюс, положение каждой характерной точки местности определяют с помощью полярных координат, к которым относятся: угол между линией теодолитного хода и направлением на снимаемую точку, а также расстояние до нее. На местности с помощью теодолита от ориентирной линии измеряют полярные углы bi, расстояние Si – рулеткой (рис. 6,а). На план точки наносят с помощью транспортира и линейки. Центр транспортира совмещают с полюсом (точкой теодолитного хода), нулевой отсчет устанавливают по ориентирному направлению (стороне теодолитного хода), и от него по ходу часовой стрелки отмечают величины углов. По полученным направлениям в масштабе плана откладывают расстояния, получают снимаемые точки (рис. 6,б).
| Рис. 6. Способ полярных координат
|
Способ угловой засечки
В способе угловой засечки по стороне теодолитного хода рулеткой измеряется произвольное расстояние, например 75 м (рис. 7,а). В полученных точках измеряются углы между линией хода инаправлением на снимаемую точку местности. Построения на плане начинают с откладывания в масштабе измеренного расстояния (75 м соответствует 15 см). В полученных точках, с помощью транспортира, строят углы от твердой линии теодолитного хода. Положение искомой точки будет в месте пересечения двух направлений (рис. 7,б).
| Рис. 7. Способ угловой засечки
| 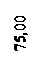 Способ линейной засечки Способ линейной засечки
В способе линейной засечки рулеткой измеряются расстояние по стороне теодолитного хода (30 м), а также расстояния до снимаемой точки (рис. 8,а). Нанесение на плане точки, снятой данным способом, заключается в построении треугольника по трем известным сторонам, из которых одна является базисом (30 м – в масштабе плана 6 см), две других берутся циркулем, и в пересечении дуг, описанных из концов базиса, получается положение снятой точки (рис. 8,б).
| Рис. 8. Способ линейной засечки
|
Способ створов
Способ применяется, когда сторону (створ) теодолитного хода пересекает линейное сооружение или контур местности. В процессе съемки рулеткой измеряют расстояния по стороне теодолитного хода от станции до пересечения с объектом местности (рис. 9.а). При построениях, линейкой откладывают эти расстояния, переведенные в масштаб плана (рис. 9,б).
После нанесения всех точек ситуации все дополнительные построения (перпендикуляры, дуги и т.п.) вытирают резинкой, оставляя только объекты местности.
 Приложение Г Приложение Г
Приложение Д
|
|
| Журнал
|
| |
|
| измерения горизонтальных углов теодолитного хода
|
| | № точ
| № точ
| Круг
| Отсчеты по
| Значение
| Значение
| Длины
| Угол
| Схема
| | ки
| ки
|
| горизонтальному
| угла в
| угла
| сторон
| наклона
| угла
| | стоя
| визиро
|
| кругу
| полу-
| в
|
|
|
| | ния
| вания
|
|
| /
| //
| приеме
| приеме
|
| 0 / //
|
| |
|
|
|
|
|
|
|
|
| |
|
|
| Основной ход
|
|
|
| |
|
| КП
|
|
|
| 118 35
|
| 1-2
|
|
| |
|
|
|
|
|
|
| 118 35 30
| 108,75
| - 1º42¢
|
| |
|
| КЛ
|
|
|
| 118 36
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
| КП
|
|
|
|
|
| 2-3
|
|
| |
|
|
|
|
|
|
|
| 50,06
| - 1º47¢
|
| |
|
| КЛ
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
| КП
|
|
|
|
|
| 3-4
|
|
| |
|
|
|
|
|
|
|
| 148,32
| +0º15¢30¢¢
|
| |
|
| КЛ
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
| КП
|
|
|
|
|
| 4-5
|
|
| |
|
|
|
|
|
|
|
| 104,47
| +1º58¢
|
| |
|
| КЛ
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
| КП
|
|
|
|
|
| 5-1
|
|
| |
|
|
|
|
|
|
|
| 81,45
| +0º26¢30¢¢
|
| |
|
| КЛ
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
| Диагональный ход
|
|
|
| |
|
| КП
|
|
|
|
|
| 3-6
|
|
| |
|
|
|
|
|
|
|
| 70,48
| +1º20¢
|
| |
|
| КЛ
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
| КП
|
|
|
|
|
| 6-7
|
|
| |
|
|
|
|
|
|
|
| 49,34
| +1º49¢30¢¢
|
| |
|
| КЛ
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
| КП
|
|
|
|
|
| 7-5
|
|
| |
|
|
|
|
|
|
|
| 66,60
| +1º37¢
|
| |
|
| КЛ
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
| КП
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
| КЛ
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
| Вычислял
|
|
|
|
Приложение Е
Варианты индивидуальных заданий.
| Дирек. Угол
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| Дирек. Угол
Х
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| Дирек. Угол
У
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| Дирек. Угол
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| | Х
| У
| Х
| У
| Х
| У
| Х
| У
| | Вариант 1
| Вариант 2
| Вариант 3
| Вариант 4
| | 250 36/ 30//
| 354,85
| 549,67
| 56,877
| 1570 38/ 00//
| 3 54,85
| 549,67
| 29,781
| 2670 26/ 00//
| 354,85
| 549,67
| 33,675
| 3480 36/ 00//
| 354,85
| 549,67
| 66,548
| | Дирек. Угол
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| Дирек. Угол
Х
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| Дирек. Угол
У
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| Дирек. Угол
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| | Х
| У
| Х
| У
| Х
| У
| Х
| У
| | Вариант 5
| Вариант 6
| Вариант 7
| Вариант 8
| | 470 56/ 30//
| 354,85
| 549,67
| 28,254
| 1640 54/ 30//
| 354,85
| 549,67
| 38,254
| 2470 23/ 00//
| 354,85
| 549,67
| 26,874
| 3540 28/ 00//
| 354,85
| 549,67
| 26,874
| | Дирек. Угол
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| Дирек. Угол
Х
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| Дирек. Угол
У
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| Дирек. Угол
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| | Х
| У
| Х
| У
| Х
| У
| Х
| У
| | Вариант 9
| Вариант 10
| Вариант 11
| Вариант 12
| | 1060 14/ 00//
| 354,85
| 549,67
| 55,542
| 870 06/ 30//
| 354,85
| 549,67
| 35,847
| 1340 28/ 00//
| 354,85
| 549,67
| 36,487
| 2690 16/ 00//
| 354,85
| 549,67
| 35,495
| | Дирек. Угол
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| Дирек. Угол
Х
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| Дирек. Угол
У
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| Дирек. Угол
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| | Х
| У
| Х
| У
| Х
| У
| Х
| У
| | Вариант 13
| Вариант 14
| Вариант 15
| Вариант 16
| | 3010 10/ 00//
| 445,26
| 510,74
| 23,451
| 1270 05/ 30//
| 445,26
| 510,74
| 84,512
| 890 31/ 30//
| 445,26
| 510,74
| 66,450
| 1030 50/ 30//
| 445,26
| 510,74
| 39,512
|
Продолжение приложения Е
Варианты индивидуальных заданий
| Дирек. Угол
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| Дирек. Угол
Х
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| Дирек. Угол
У
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| Дирек. Угол
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| | Х
| У
| Х
| У
| Х
| У
| Х
| У
| | Вариант 17
| Вариант 18
| Вариант 19
| Вариант 20
| | 2070 57/ 00//
| 445,26
| 510,74
| 45,127
| 1360 12/ 30//
| 445,26
| 510,74
| 51,358
| 2170 01/ 00//
| 445,26
| 510,74
| 55,554
| 3040 05/ 00//
| 445,26
| 510,74
| 66,514
| | Дирек. Угол
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| Дирек. Угол
Х
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| Дирек. Угол
У
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| Дирек. Угол
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| | Х
| У
| Х
| У
| Х
| У
| Х
| У
| | Вариант 21
| Вариант 22
| Вариант 23
| Вариант 24
| | 1360 31/ 00//
| 445,26
| 510,74
| 48,517
| 1640 35/ 30//
| 445,26
| 510,74
| 48,594
| 2680 26/ 00//
| 445,26
| 510,74
| 66,457
| 970 44/ 30//
| 445,26
| 510,74
| 67,124
| | Дирек. Угол
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| Дирек. Угол
Х
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| Дирек. Угол
У
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| Дирек. Угол
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| | Х
| У
| Х
| У
| Х
| У
| Х
| У
| | Вариант 25
| Вариант 26
| Вариант 27
| Вариант 28
| | 340 33/ 00//
| 542,39
| 359,75
| 55,627
| 1400 25/ 00//
| 542,39
| 359,75
| 42,328
| 2600 58/ 30//
| 542,39
| 359,75
| 33,549
| 3170 51/ 00//
| 542,39
| 359,75
| 38,451
| | Дирек. Угол
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| Дирек. Угол
Х
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| Дирек. Угол
У
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| Дирек. Угол
| Коор-ты
нач-ной
точки,
м
| Отметка,м
| | Х
| У
| Х
| У
| Х
| У
| Х
| У
| | Вариант 29
| Вариант 30
| Вариант 31
| Вариант 32
| | 2380 23/ 00//
| 542,39
| 359,75
| 20,854
| 1870 08/ 30//
| 542,39
| 359,75
| 60,541
| 760 06/ 30//
| 542,39
| 359,75
| 39,543
| 3340 07/ 30//
| 542,39
| 359,75
| 45,521
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ПриложениеЖ
|
| | Ведомость вычисления координат вершин замкнутого теодолитного хода
|
| |
| | Верши
на хода
| Измеренные углы
| Исправленные углы
| Дирекционные углы
| Румбы, r
| Гориз.
Проло
жение
| Приращения координат
| Координаты
|
| | вычисленные
| исправленные
|
| |
| /
| //
|
| /
| //
|
| /
| //
|
|
|
| D х
| D у
| D х
| D у
| X
| Y
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | åbпр
|
|
|
|
|
|
|
|
|
|
|
|
| Р=
|
|
|
|
|
|
|
| | åbт
|
|
|
|
|
|
|
|
|
|
|
|
|
| fΔx =
| fΔу=
|
|
|
|
|
| | ¦b
|
|
|
|
|
|
|
|
|
|
|
|
|
| fабс=
|
|
|
|
|
|
| | ¦bдоп
| ±
| 2,2
|
|
|
|
|
|
|
|
|
|
|
| fотн=
| 1/
| < 1/2000
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Приложение З
|
| | Ведомость вычисления координат вершин диагонального теодолитного хода
|
| |
| | Вершина хода
| Измеренные углы
| Исправленные углы
| Дирекционные углы
| Румбы, r
| Горизонталь
ное
проложение
| Приращения координат
| Координаты
|
| | вычисленные
| исправленные
|
| |
| /
| //
|
| /
| //
|
| /
| //
|
|
|
| D х
| D у
| D х
| D у
| X
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | åbпр
|
|
|
|
|
|
|
|
|
|
|
|
|
| fΔx =
| fΔу=
|
|
|
|
|
| | åbт
|
|
|
|
|
|
|
|
|
|
|
|
|
| fабс=
|
|
|
|
|
|
| | ¦b
|
|
|
|
|
|
|
|
|
|
|
|
|
| fотн=
| 1/
| < 1/1000
|
|
|
|
| | ¦bдоп
| ±
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| Вычисл |
|
Поиск по сайту:
|

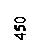 Необходимо нанести на план точку 1 с координатами
Необходимо нанести на план точку 1 с координатами 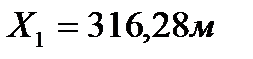 и
и 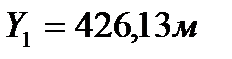 . Сначала выясняют, в каком из квадратов должна лежать эта точка: по направлению X точка должна находится между линиями сетки с абсциссами 300 и 350 м, по направлению Y - между линиями сетки с ординатами 400 и 450 м (рис. 3). От линии с абсциссой 300 по вертикальным сторонам этого квадрата вверх откладывают расстояние 316,28-300 =16,28 м переведенное в масштаб плана (3,25 см) и проводят линию, параллельную линии с абсциссой 300 м. Вдоль нее от вертикальной линии сетки с ординатой 400 м откладывают вправо расстояние 426,13-400=26,13 м переведенное в масштаб плана (5,2 см).
. Сначала выясняют, в каком из квадратов должна лежать эта точка: по направлению X точка должна находится между линиями сетки с абсциссами 300 и 350 м, по направлению Y - между линиями сетки с ординатами 400 и 450 м (рис. 3). От линии с абсциссой 300 по вертикальным сторонам этого квадрата вверх откладывают расстояние 316,28-300 =16,28 м переведенное в масштаб плана (3,25 см) и проводят линию, параллельную линии с абсциссой 300 м. Вдоль нее от вертикальной линии сетки с ординатой 400 м откладывают вправо расстояние 426,13-400=26,13 м переведенное в масштаб плана (5,2 см).
 Способ линейной засечки
Способ линейной засечки
 Приложение Г
Приложение Г