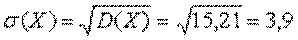ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«ОРЕНБУРГСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ»
Кафедра « Автоматизированные системы обработки информации и управления »
ТЕМА
«Некоторые распределения НСВ и ДСВ»
Исследовательская работа по дисциплине
«Теория вероятности и математическая статистика»
Выполнил:
студент 2 курса
группа: ИВТ
Брынцев Олег Сергеевич
Научный руководитель:
Павлидис В.Д.
Оренбург 2016
1. Определение закона распределения:
1.1 НСВ (непрерывной случайной величины)
1.2 ДСВ (дискретной случайной величины)
2. Условия распределения:
2.1 НСВ
2.1.1 Равномерное распределение
2.1.2 Нормальное распределение
3. Числовые характеристики НСВ и ДСВ:
3.1 Математическое ожидание
3.2 Дисперсия
3.3 Среднее квадратическое отклонение
4. Задачи:
4.1 НСВ
4.2 ДСВ
Определение закона распределения
НСВ
Если рассматривать случайную величину Х, значения которой заполняют интервал (a,b) и составить перечень всех возможных её значений невозможно, то она называется непрерывной.
ДСВ
Законом распределения дискретной случайной величины называют соответствие между полученными значениями дискретной случайной величины и их вероятностями. Его можно задать:
1) таблично (рядом распределения);
2) графически;
3) аналитически (в виде формулы).
Условия распределения
НСВ
Равномерное распределение
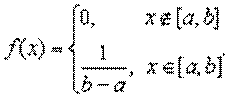
Непрерывная случайная величина Х называется распределенной равномерно на отрезке [a,b], если её плотность распределения вероятностей постоянна на данном отрезке:
Функция распределения в этом случае примет вид:
|
|
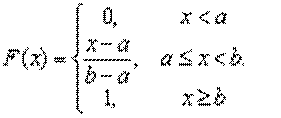
Нормальное распределение
Непрерывная случайная величина - x имеет нормальное распределение с параметрами: m, s>0, если плотность распределения вероятностей имеет вид:
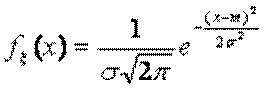
где: m – математическое ожидание, s – среднеквадратическое отклонение.
Нормальное распределение называют еще гауссовским по имени немецкого математика Гаусса. Тот факт, что случайная величина имеет нормальное распределение с параметрами: m, s, обозначают так: N (m,s), где:
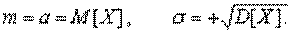
Достаточно часто в формулах математическое ожидание обозначают через а. Если случайная величина распределена по закону N(0,1), то она называется нормированной или стандартизированной нормальной величиной. Функция распределения для нее имеет вид:
График плотности представлен ниже:
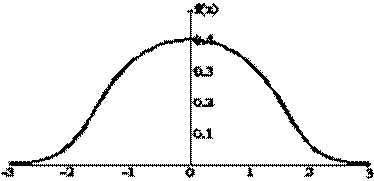
3. Числовые характеристики НСВ1 и ДСВ2
3.1 Математическое ожидание1
Числовые характеристики случайной величины X равномерно распределенной на интервале (a,b):
Математическое ожидание М(Х) 2 дискретной случайной величины Х это сумма произведений всех возможных значений величины Х на соответствующие вероятности:
| М(Х) = x1· p1 + x2· p2 + … + xn· pn. |
Свойства математического ожидания:
1. Математическое ожидание имеет ту же размерность, что и сама случайная величина.
2. Математическое ожидание может быть как положительным, так и отрицательным числом.
3. Математическое ожидание постоянной величины С равно этой постоянной. М (С) = С.
4. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий этих величин.
|
|
М (X + Y +... + W) = М (X) + М (Y) +... + М (W).
5. Математическое ожидание произведения двух или нескольких взаимно независимых случайных величин равно произведению математических ожиданий этих величин.
М (XY) = M(X) × M(Y).
6. Постоянный множитель можно выносить за знак математического ожидания:
М(СХ) = С× М(Х).
3.2 Дисперсия1
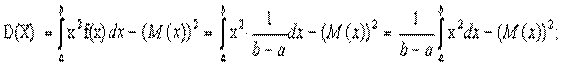
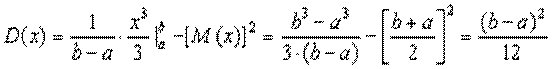
Дисперсия D(X) 2 дискретной случайной величины Х – это математическое ожидание квадрата отклонения случайной величины Х от ее математического ожидания:
| D(X) = M [X – M(X)]2. |
Формула (5.5) после возведения в степень и преобразований имеет вид:
| D(X) = M (X2) – [M(X)]2. |
Свойства дисперсии:
Дисперсия имеет размерность, равную квадрату размерности случайной величины.
Дисперсия постоянной величины всегда равна нулю: D (С) = 0.
Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D (СX) = С2×D(X).
Дисперсия алгебраической суммы двух независимых случайных величин равна сумме их дисперсией: D(X +Y) = D(X) + D(Y).
3.3 Среднее квадратическое отклонение1
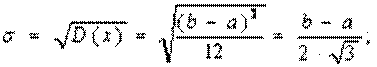
Среднее квадратическое отклонение s(Х) дискретной случайной величины Х определяется формулой (5.2). Среднее квадратическое отклонение имеет ту же размерность, что и случайная величина.
Случайная величина называется центрированной, если математическое ожидание M(X)=0, и стандартизированной, если M(X)=0 и среднее квадратическое отклонение s = 1.
Примеры задач
НСВ
Найти дисперсию и среднее квадратическое отклонение случайной величины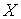 
равномерно распределенной на интервале [2; 6].
|
|
Решение:
Математическое ожидание:
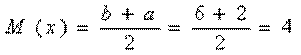
Дисперсия:
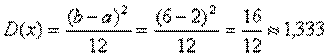
Среднее квадратическое отклонение:
ДСВ
Найти математическое ожидание М (Х), дисперсию D(Х) и среднее квадратическое отклонение s(Х) дискретной случайной величины Х, заданной законом распределения в таблице:
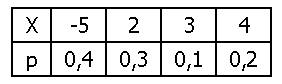
Решение:
Математическое ожидание:
М(Х)= –5× 0,4 + 2× 0,3 + 3× 0,1 + 4× 0,2 = -0,3
Дисперсия:
D(Х) = М(Х2) – [М(Х)]2
Закон распределения квадрата Х2 случайной величины задан в таблице:
Математическое ожидание Х2:
М(Х2) = 25×0,4 + 4×0,3 + 9× 0,1 + 16×0,2 = 15,3.
Искомая дисперсия:
D(Х) = М(Х2) – [М(Х)]2 = 15,3 – (– 0,3)2 = 15,21.
Среднее квадратическое отклонение:
