Лабораторная работа № 29
 |
Рис. 29.1. Экспериментальная установка для исследования гидравлического
сопротивления и пропускной способности напорных коротких труб
Цель работы – экспериментальное исследование гидравлического сопротивления и пропускной способности напорных коротких труб круглого и квадратного сечения.
Водопропускные трубы могут быть напорными, полунапорными и безнапорными. К напорным водопропускным трубам относятся трубы полностью заполненные водой, при этом уровень свободной поверхности воды перед входом в такую трубу находится выше отметки её потолка. Такие трубы называют также напорными трубопроводами. Как показала практика напорный режим течения в трубе имеет место при
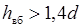 или или 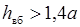 , ,
| (29.1) |
где h вб – глубина воды перед входом в трубу; d и a – диаметр круглой (рис. 29.1), высота прямоугольной или сторона квадратной (рис. 29.2) трубы.

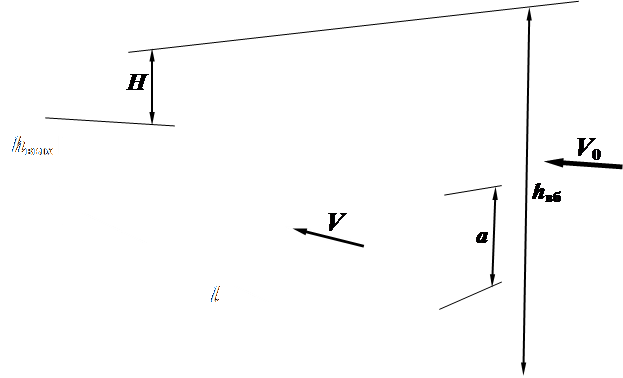 |
Рис. 29.2. Экспериментальная установка с трубой квадратного сечения
Снижение напора в напорных трубах при преодолении гидравлических сопротивлений называют гидравлическими потерями и обозначают h w. Гидравлические потери делят на два типа:
– потери напора по длине прямых участков труб постоянного поперечного сечения с равномерным течением в них (линейные потери)
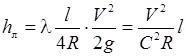 , ,
| (29.2) |
затрачиваемые на преодоление сопротивления вязкого трения жидкости о стенки трубопровода;
– местные потери напора (вихревые потери)
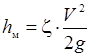 , ,
| (29.3) |
вызванные такими элементами трубопроводов, в которых вследствие изменения размеров или конфигурации труб происходит изменение вектора скорости течения (его модуля или направления), трансформация профиля скоростей течения, формирование вихревых зон и зон отрыва потока от стенок.
В формулах Дарси – Вейсбаха (29.2) и Вейсбаха (29.3): l и z – коэффициенты гидравлического трения и местного сопротивления, при гидравлических расчетах определяемые по справочным данным [2, 3, 6, 7]; g – ускорение свободного падения, g = 9,81 м/с2; l и R – соответственно длина и гидравлический радиус трубопроводов круглого
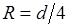
| (29.4) |
и квадратного сечения
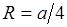 ; ;
| (29.5) |
V – средняя (среднерасходная) скорость потока
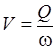 ; ;
| (29.6) |
Q – пропускаемый по трубе расход; w – площадь поперечного сечения трубы на прямом участке или после местного сопротивления
– для трубы круглого сечения
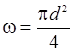 , ,
| (29.7) |
– для квадратной трубы
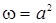 ; ;
| (29.8) |
С – коэффициент Шези
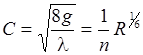 ; ;
| (29.9) |
n – коэффициент шероховатости стенок трубы, при гидравлических расчетах определяемый по справочным данным [2, 3, 6, 7].
При расчете потерь напора в трубопроводе используется принцип сложения, согласно которому общие гидравлические потери равны сумме потерь на гидравлическое трение по длине участков с равномерным движением жидкости и на всех местных гидравлических сопротивлениях
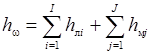 , ,
| (29.10) |
где I и J – количество прямых участков трубопровода с постоянным поперечным сечением и местных гидравлических сопротивлений по его трассе.
При 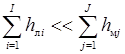 трубопроводы называют весьма короткими, при
трубопроводы называют весьма короткими, при 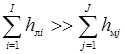 – длинными. В первом случае при гидравлическом расчете учитываются только местные потери напора, во втором – только линейные.
– длинными. В первом случае при гидравлическом расчете учитываются только местные потери напора, во втором – только линейные.
В настоящей лабораторной работе рассматривается наиболее общий случай, при котором следует учитывать суммарные гидравлические потери, как по длине, так и местные в соответствии с равенством (29.10). Такие трубопроводы называюткороткими.
Рассмотрим два типичных напорных коротких трубопровода: круглого и квадратного поперечного сечения. На лабораторной экспериментальной установке, показанной на рис. 29.1 – 29.3, длина труб составляет l = 1,21 м, при этом труба круглого сечения имеет диаметр равный d = 150 мм, квадратная труба имеет размеры поперечного сечения а = 133 на 133 мм. При этом площадь поперечного сечения круглой и квадратной труб одинакова w = 0,017671 м2.

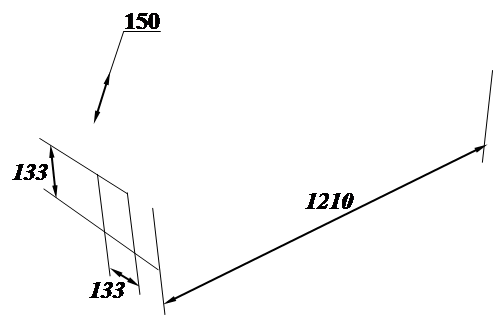 |
Рис. 29.3. Основные конструктивные размеры экспериментальных коротких труб круглого и квадратного сечения (размеры в миллиметрах)
Поскольку трубы экспериментальной лабораторной установки имеют постоянное сечение по длине, то гидравлические потери в них составляют
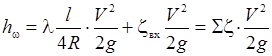 , ,
| (29.11) |
где Sz – суммарный коэффициент гидравлического сопротивления трубы
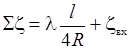 ; ;
| (29.12) |
zвх – коэффициент гидравлического сопротивления на входе потока в трубу
 ; ;
| (29.13) |
e – коэффициент сжатия потока на входе в трубу
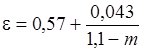 ; ;
| (29.14) |
m – отношение площади поперечного сечения трубы к площади живого сечения потока перед входом в трубу в верхнем бьефе
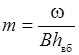 ; ;
| (29.15) |
В – ширина русла или канала в верхнем бьефе перед входом в трубу, равная на модели ширине лабораторного лотка В = 311 мм (см. рис. 29.1 и 29.2).
Пропускная способность напорных коротких труб, т.е. пропускаемый ими расход, вычисляется по формуле
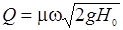 , ,
| (29.16) |
полученной с использованием уравнения Бернулли, записанного для сечений в верхнем бьефе перед входом в трубу и на её выходе (см. рис. 29.1 и 29.2)
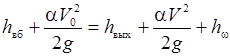 , ,
| (29.17) |
гдеa – коэффициент Кориолиса, a = 1,03; h вых – глубина потока на выходе из трубы; V 0 – средняя скорость потока в верхнем бьефе на подходе к трубе
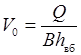 ; ;
| (29.18) |
m – коэффициент расхода трубы
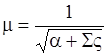 ; ;
| (29.19) |
Н 0 – гидродинамический напор, равный разности горизонтов воды перед входом и выходом трубы с учетом скоростного напора в верхнем бьефе
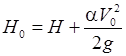 ; ;
| (29.20) |
Н – геометрический (гидростатический) напор
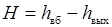 . .
| (29.21) |
При гидравлическом расчете потерь напора и пропускной способности трубы её размеры d или a, ширина канала B, где она установлена, а также гидродинамический напор Н 0 и глубина в верхнем бьефе h вб должны быть известны или заданы. В этом случае вычисления выполняют прямым счетом в соответствии с изложенным методом. А именно: согласно справочным данным [2, 3, 6, 7] определяют или вычисляют коэффициенты гидравлического трения l, шероховатости стенок трубы n, Шези С, гидравлического сопротивления на входе потока в трубу zвх, суммарный коэффициент гидравлического сопротивления трубы Sz, коэффициент расхода m; после чего находят величину пропускаемого расхода Q, потерь напора в трубе h w и глубину потока на выходе из трубы h вых. В заключении по формуле А.Д. Альтшуля [6] вычисляют потери напора на начальном участке канала нижнего бьефа при внезапном расширении потока после выхода из трубы
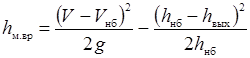 , ,
| (29.22) |
где h нб – глубина потока в отводящем канале нижнего бьефа (см. рис. 29.1); V нб – скорость потока в отводящем канале нижнего бьефа
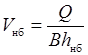 . .
| (29.23) |
При малой разнице в глубинах h нб и h вых формула А.Д. Альтшуля (29.22) сводится к формуле Борда [3, 6, 7]
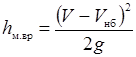 . .
| (29.24) |
Если вместо гидродинамического напора Н 0 известна или задана глубина потока в отводящем канале нижнего бьефа h нб (см. рис. 29.1), то алгоритм расчета после определения коэффициентов l, n, С, zвх, Sz и m изменяется. Задается пропускаемый трубой расход Q, по которому, согласно равенству (29.16) вычисляют гидродинамический напор Н 0, а затем – критическую глубину потока
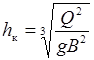 , ,
| (29.25) |
и глубину потока на выходе из трубы
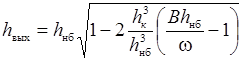 . .
| (29.26) |
Последняя формула получена из уравнений А.Д. Альтшуля (29.22) и Бернулли
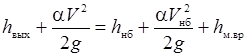 , ,
| (29.27) |
записанного для створов выхода потока из трубы и в конце начального участка канала нижнего бьефа, при этом в уравнении (29.27) принимается a = 1,00.
Дальнейший расчет потерь напора в трубе h w и на начальном участке канала нижнего бьефа h м.вр остаётся прежним.
Из равенств (29.2) и (29.6) также следует, что скоростная характеристика напорной прямой трубы постоянного сечения равна
 , ,
| (29.28) |
а её расходная характеристика (модуль расхода) составляет
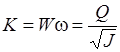 , ,
| (29.29) |
где J – гидравлический уклон напорной прямой трубы постоянного сечения
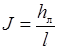 . .
| (29.30) |
Таким образом, пропускная способность напорного трубопровода может также определяться по его модулю расхода и гидравлическому уклону
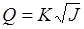 . .
| (29.31) |
Основной задачей лабораторной работы является расчетно-опытная проверка соответствия изложенного метода гидравлического расчета сопротивления и пропускной способности напорных коротких труб круглого и квадратного сечения экспериментальным данным.
Следует отметить, что изложенный метод гидравлического расчета справедлив только при турбулентном движении жидкости в области квадратичного сопротивления труб (автомодельной области) при высоких числах Рейнольдса
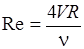 , ,
| (29.32) |
где n – коэффициент молекулярной кинематической вязкости воды, функция связи коэффициента кинематической вязкости с температурой воды приведена в справочнике [6, стр. 13, табл. б/н]. Таким образом, на натурных объектах при высоких скоростях и линейных размерах потоков изложенный метод расчета справедлив, на лабораторных моделях – не всегда. Такое обстоятельство следует учитывать при анализе полученных экспериментальных результатов, выделяя область квадратичного сопротивления, в которой коэффициенты сопротивлений перестают зависеть от числа Рейнольдса. В этом случае говорят течение автомодельно по Рейнольдсу.
Методика выполнения лабораторной работы.
1. Перед выполнением лабораторной работы установите гидравлический лоток и регулируемый переливной порог в его отводящем участке в горизонтальное положение. В средней части рабочего участка лотка установите модель короткой напорной водопропускной трубы круглого поперечного сечения (рис. 29.1). Модель установите таким образом, чтобы иметь возможность выполнять измерения глубин потока в верхнем бьефе перед входом в трубу (h вб), на выходе из неё (h вых) и в отводящем канале нижнего бьефа (h нб) одновременно с помощью шпиценмасштабов и по пьезометрическому щиту. Обратите внимание на направление движения потока по лотку. Выгните резиновые уплотнения напорной грани модели навстречу движению потока воды в лотке, а резиновые уплотнения низовой грани – против движения потока. Уплотнения не должны быть скручены и должны прилегать к стеклянным стенкам лотка. Убедитесь, что после монтажа модели в лотке не осталось незакрепленных или посторонних предметов, например, винтов, инструментов, протирочных материалов.
2. На трех инструментальных каретках установите электронные шпиценмасштабы (см. рис. 1.6 в лабораторной работе № 1). Для измерения глубины потока в верхнем бьефе (h вб) расположите первую каретку перед моделью короткой напорной трубы таким образом, чтобы игла шпиценмасштаба находилась на расстоянии L = -0,500 м от напорной грани модели. Вторую каретку с электронным шпиценмасштабом установите в створе выходного сечения трубы для измерения глубины h вых (рис. 29.1 и 29.2). Третью каретку с электронным шпиценмасштабом расположите в нижнем бьефе на таком расстоянии от выходного сечения трубы, на котором глубина потока в лотке стабилизируется и может приниматься равной глубине в отводящем канале нижнего бьефа h нб (рис. 29.1). Выставьте нули всех шпиценмасштабов по отметкам дна лотка в створах измерения перечисленных глубин.
3. На пульте управления режимом работы лабораторного лотка или управляющем компьютере задайте пропускаемый по лотку расход 5÷10 м3/час. Включите насос лотка.
4. Регулирующим переливным порогом в отводящем участке лотка надвиньте гидравлический прыжок на низовую грань модели короткой трубы. Отрегулируйте положение гидравлического прыжка таким образом, чтобы глубина потока на выходе из трубы h вых (рис. 29.1 и 29.2) обеспечивала подтопление её выходного сечения, при котором отметка потолка трубы ниже отметки уровня свободной поверхности потока в нижнем бьефе. Это позволяет получить напорное течение жидкости по всей длине трубы.
5. Перед выполнением программы опытов выполните измерение температуры воды в лотке и определите её коэффициент кинематической вязкости n, для определения коэффициента кинематической вязкости воды используйте данные справочника [6, стр. 13, табл. б/н]. Запишите температуру и вязкость воды в строку над табл. 29.1 (приведена ниже) при выполнении опытов на круглой трубе или в строку над табл. 29.3 (приведена ниже) при выполнении опытов на квадратной трубе.
6. После стабилизации уровня верхнего бьефа перед моделью напорной короткой трубы и гидравлического режима работы лотка (время стабилизации около трех – пяти минут) выполните измерения и запишите в строку табл. 29.1, соответствующую номеру опыта (№), следующих экспериментальных данных:
- пропускаемого расхода Q (измеряется электромагнитным расходомером класса точности 0,3 с диапазоном измерений 0÷150 м3/час);
- глубины потока в верхнем бьефе h вб (измерение производится электронным шпиценмасштабом, выставленным на ноль на отметке дна лотка);
- глубины потока в лотке на выходе из трубы h вых (измерение производится вторым электронным шпиценмасштабом, выставленным на ноль на отметке дна лотка);
- глубины потока в отводящем канале нижнего бьефа h нб (измерение производится третьим электронным шпиценмасштабом, выставленным на ноль на отметке дна лотка).
7. Увеличьте расход потока на 5÷10 м3/час.
8. Далее повторите действия от пункта 6 до пункта 7. Повторите опыты несколько раз. Последний эксперимент выполните при предельно высоком расходе около 115 м3/час.
9. После выполнения пункта 8 выключите насос и производите перемонтаж экспериментальной установки. Для этого перевернув кульверт, замените рабочую напорную короткую трубу круглого сечения на трубу квадратного сечения. После выполнения перемонтажа убедитесь, что в лотке не осталось незакрепленных или посторонних предметов, например, винтов, инструментов, протирочных материалов.
10. Далее повторите действия от пункта 3 до пункта 8 включительно. При выполнении пункта 6 измеренные значения расхода Q и глубин h вб, h вых и h нб запишите в табл. 29.3 для трубы квадратного сечения.
11. После выполнения программы опытов выключите насос и приборы.
12. Далее выполните камеральную обработку и анализ результатов проведенных экспериментальных исследований.
13. В табл. 29.1 и 29.3 наряду с непосредственно измеренными значениями расходов Q и глубин h вб, h вых, h нб запишите результаты вычислений:
– гидродинамических напоров Н 0 (см. формулу (29.20));
– коэффициентов расхода m, приводя формулу (29.16) к виду,
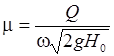 ; ;
| (29.33) |
– суммарных коэффициентов гидравлического сопротивления труб
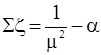 , ,
| (29.34) |
гдеa – коэффициент Кориолиса, a = 1,03;
– суммарных гидравлических потерь в трубах h w (см. формулу (29.11));
– коэффициентов гидравлического сопротивления на входе в трубу zвх (см. формулу (29.13));
– коэффициентов гидравлического трения, приводя формулу (29.16) к виду,
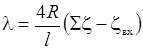 ; ;
| (29.35) |
– коэффициентов шероховатости труб, равных согласно (29.9)
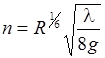 ; ;
| (29.36) |
– скоростных характеристик (W) и модулей расхода (K) напорных коротких труб круглого и квадратного сечений (см. формулы (29.9), (29.28) и (29.29));
– гидравлических потерь на начальном участке канала нижнего бьефа при внезапном расширении потока после выхода из трубы h м.вр (см. формулу (29.22));
– коэффициентов гидравлического сопротивления при выходе потока из трубы в канал нижнего бьефа
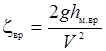 , ,
| (29.37) |
отнесенных к скоростному напору потока в трубе;
– чисел Рейнольдса (см. формулу (29.32).
14. В табл. 29.2 и 29.4 (приведены ниже) в соответствии с конструктивными размерами моделей напорных коротких труб круглого и квадратного сечения и изменяемыми в процессе опытов исходными данными, в число которых входят значения варьируемых расходов Q и глубин потока в верхнем h вб и нижнем h нб бьефах (см. табл. 29.1 и 29.3) вычислите и запишите расчетные значения:
- коэффициентов гидравлического сопротивления входных сечений труб zвх (см. формулу (29.13));
- коэффициентов Шези С (см. формулу (29.9)), где коэффициент шероховатости принят по справочным данным [2, 3 6, 7] равным n = 0,009;
- коэффициентов гидравлического трения по длине l (см. формулу (29.9), приведённую к виду)
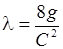 ; ;
| (29.38) |
- расчетных скоростных характеристик (W) и модулей расхода (K) напорных коротких труб круглого и квадратного сечений (см. формулы (29.9), (29.28) и (29.29));
- суммарных коэффициентов гидравлического сопротивления труб Sz (см. формулу (29.12));
- гидравлических потерь в коротких напорных трубах круглого и квадратного сечения h w (см. формулу (29.11));
- коэффициентов расхода m (см. формулу (29.19));
- гидродинамических напоров Н 0 (см. формулу (29.16), приводя её к виду)
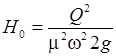 ; ;
| (29.39) |
- глубины потока в лотке на выходе из трубы h вых, приводя формулы (29.20) и (29.21) к расчетному равенству
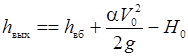 ; ;
| (29.40) |
- гидравлических потерь на начальном участке канала нижнего бьефа при внезапном расширении потока после выхода из трубы h м.вр (см. формулу (29.22));
- коэффициентов гидравлического сопротивления при выходе потока из трубы в канал нижнего бьефа, отнесенных к скоростному напору потока в трубе (см. формулу (29.37)).
15. По результатам вычислений табл. 29.1 – 29.4 на двух листах миллиметровой бумаги формата А4 (210´297 мм) отдельно для каждой трубы постройте графики экспериментальных и расчетных напор – расходных Q – H 0 характеристик коротких труб круглого и квадратного сечения (H 0 = f (Q)). На графиках покажите экспериментальные точки замеров, расчетные графики покажите сплошными плавными линиями тренда. На тех же форматках покажите экспериментальные (точки) и расчетные (сплошные плавные линии тренда) графики экспериментальных и расчетных суммарных гидравлических потерь в пределах проточного тракта труб h w = f (Q) и потерь за их пределами на выходе в нижний бьеф h м.вр = f (Q).
16. По результатам вычислений табл. 29.1 и 29.3 на двух листах миллиметровой бумаги формата А4 (210´297 мм) постройте графики функций изменения от числа Рейнольдса (Re) следующих экспериментальные характеристик коротких напорных труб круглого и квадратного сечения:
– на первом листе для исследованных труб покажите графики коэффициентов их гидравлического трения (l = f (Re)), коэффициентов шероховатости (n = f (Re)), коэффициентов гидравлического сопротивления на входе (zвх = f (Re)), и коэффициентов внезапного расширения на выходе (zвр = f (Re));
– на втором листе для исследованных труб покажите графики их коэффициентов расхода (m = f (Re)), скоростных характеристик (W = f (Re)) и модулей расхода (K = f (Re)).
На графиках укажите экспериментальные точки замеров, которые соединяются плавными линиями тренда. Графики, относящиеся к трубам разного сечения, показываются разным цветом карандаша.
17. Выполните сопоставительный анализ экспериментальных и расчетных данных. Дайте оценку соответствия экспериментальных и расчетных данных: хорошее соответствие, удовлетворительное, несоответствие.
Таблица 29.1. Экспериментальное исследование гидравлических сопротивлений и пропускной способности
напорной короткой трубы круглого сечения диаметром d = 150 мм и длиной l = 1210 мм
(температура воды t = ______оС, коэффициент кинематической вязкости воды n =________м2/с)
| № | Опытные данные | Обработка опытных данных | ||||||||||||||
| Q, | h вб | h вых | h нб | Н 0 | m | Sz | h w | zвх | l | n | W | K | h м.вр | zвр | Re | |
| м3/час | мм | мм | мм | м | – | – | м | – | – | – | м/с | м3/с | м | – | – | |
Таблица 29.2. Расчетные гидравлические сопротивления и пропускная способность напорной
короткой трубы круглого сечения диаметром d = 150 мм и длиной l = 1210 мм
(коэффициент шероховатости трубы п = 0,009)
| № | Исходные данные | Расчетные данные | |||||||||||||
| Q, | h вб | h нб | zвх | С | l | W | K | Sz | h w | m | Н 0 | h вых | h м.вр | zвр | |
| м3/час | м | м | – | м0,5/с | – | м/с | м3/с | – | м | – | м | м | м | – | |
Таблица 29.3. Экспериментальное исследование гидравлических сопротивлений и пропускной способности
напорной короткой трубы квадратного сечения с размерами а = 133 на 133 мм и длиной l = 1210 мм
(температура воды t = ______оС, коэффициент кинематической вязкости воды n =________м2/с)
| № | Опытные данные | Обработка опытных данных | ||||||||||||||
| Q, | h вб | h вых | h нб | Н 0 | m | Sz | h w | zвх | l | n | W | K | h м.вр | zвр | Re | |
| м3/час | мм | мм | мм | м | – | – | м | – | – | – | м/с | м3/с | м | – | – | |
Таблица 29.4. Расчетные гидравлические сопротивления и пропускная способность напорной
короткой трубы квадратного сечения с размерами а = 133 на 133 мм и длиной l = 1210 мм
(коэффициент шероховатости трубы п = 0,009)
| № | Исходные данные | Расчетные данные | |||||||||||||
| Q, | h вб | h нб | zвх | С | l | W | K | Sz | h w | m | Н 0 | h вых | h м.вр | zвр | |
| м3/час | м | м | – | м0,5/с | – | м/с | м3/с | – | м | – | м | м | м | – | |
|
| Поделиться: |
Поиск по сайту
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2016-02-16 Нарушение авторских прав и Нарушение персональных данных
Поиск по сайту:
Читайте также:
Деталирование сборочного чертежа
Когда производственнику особенно важно наличие гибких производственных мощностей?
Собственные движения и пространственные скорости звезд