Одним из основных понятий теории вероятности является понятие случайной величины. Рассмотрим некоторые примеры случайных величин:
1) число попаданий в цель при трех выстрелах.
Возможные результаты таковы: 0,1,2 или 3 раза попадания.
2) число вызовов, поступивших на телефонную станцию за сутки. Значениями может быть любое число от 1, 2, 3,….
Случайной величиной называется такая величина, которая в результате опыта может принимать различные значения, причем заранее неизвестно, какое именно, и известны вероятности, с которыми случайная величина принимает каждое конкретное значение.
Определение. Любое соотношение, устанавливающее связь между всеми возможными значениями случайной величины и их вероятностями, называется законом распределения случайной величины.
Чтобы задать случайную величину, надо указать ее закон распределения. Случайные величины принято обозначать греческими буквами x, h, q, а их возможные значения – латинскими буквами с индексами xi, yi, zi.
Пример 2.1. Обозначим буквой x число гербов, выпавших при подбрасывании монеты три раза. Это число зависит от случайных результатов подбрасывания и поэтому будет случайной величиной. В этом примере случайная величина x может принять четыре значения 0,1,2,3, но невозможно предсказать какое из них. Найдем вероятности этих значений. Пространство элементарных событий 
в этом примере состоит из восьми упорядоченных троек
={ω1 = ГГГ, ω2 = ГГЦ, ω3 = ГЦГ, ω 4= ЦГГ, ω5 = ГЦЦ, ω6 = ЦГЦ, ω7= ЦЦГ, ω8 = ЦЦЦ },
где Г обозначает выпадение герба при одном подбрасывании, а Ц – выпадение цифры.
Обозначим через Аi событие, в котором при подбрасывании монеты появились i гербов (i= 0,1,2,3). Каждое событие Аi является составным событием и содержитвсе элементарные события ωi ,которые привели к появлению i гербов:
Аi= { 
}.
Следовательно,
A 0 = {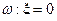 
} = { ЦЦЦ }, A 1={ 
}={ ГЦЦ, ЦГЦ, ЦЦГ },
A 2 = { 
}={ ГГЦ, ГЦГ, ЦГГ }, A 3={ 
}={ ЦЦЦ }.
Дополнительно предположим, что подбрасывают правильную монету. Тогда из независимости испытаний следует, что вероятность каждого элементарного события ω i равна 
* * = 
. Из классического определения вероятности события Ai имеют вероятности, равные
p 0 =P (A 0) = P{ЦЦЦ }= 
, p 1 =P (A 1) =P { ГЦЦ,ЦГЦ, ЦЦГ } = 
,
p 2 =P (A 2) =P { ГГЦ,ГЦГ,ЦГГ } = 
, p 3 =P (A 3) =P { ЦЦЦ } = 
.
Отметим, что все события Ai несовместны и составляют пространство элементарных несовместных событий 
, т.е.
W = A 0 +A 1 +A 2 +A 3.
Из аксиом вероятности следует равенство
р( W) = р(A 0 +A 1 +A 2 +A 3) = p (A 0) + p (A 1) + p (A 2) + p (A 3) = 1.
Составим таблицу из полученных возможных значений этой случайной величины и соответствующих вероятностей:
| ξ | ||||
| 
| 
| 
| 
|
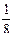
Пример 2.2. Производится один выстрел по плоской круглой мишени радиуса R. Учитываются только выстрелы, которые приводят к попаданию в мишень. В качестве случайной величины рассмотрим расстояние x от точки попадания до центра мишени. Тогда множество возможных значений случайной величины образует числовой интервал [0, R ]. Предположим, что любая точка мишени может быть поражена с одинаковой вероятностью. Отсюда следует, что с одинаковой вероятностью случайная величина x принимает любое значение из интервала [0, R ]. В этом случае вероятность того, что расстояние x не превзойдет числа x (0≤ x ≤ R), можно найти из геометрического определения вероятности по формуле R (x £ x) = x/R. Очевидно, что при x>R вероятность R (x £ x)=1, а при x <0 вероятность R (x £ x)=0.
Из приведенных примеров видно, что случайной величиной являетсяфункция f, которая каждому элементарному событию w ставит в соответствие число ¦ (w). Эти числа ¦ (w) называют возможными значениями случайной величины.
В зависимости от множества возможных значений случайной величины выделяют два типа случайных величин:
а) дискретная случайная величина – это величина, значения которой можно (пересчитать) перенумеровать;
б) непрерывная случайная величина – это такая величина, значения которой заполняют целиком некоторый промежуток числовой оси или всю числовую ось.
Определение. Функция распределения F(x) случайной величины x определяется равенством
F (x) =P (w: ¦ (w) £ x), (2.1)
для всех действительных чисел x.
В примере 2.2функция распределения определяется формулой
.