Математическое ожидание случайной величины
Закон распределения случайной величины является наиболее полной ее характеристикой. Он одновременно указывает и на значение случайной величины и на его вероятность. Однако часто в теории вероятностей и в ее приложениях большую роль играют постоянные числа, которые можно получить, используя законы распределения. В этом параграфе рассмотрим математическое ожидание или среднее значение случайной величины.
Пусть x обозначает дискретную случайную величину с рядом распределения


 xi x 1 x 2,…, xn,…
xi x 1 x 2,…, xn,…
pi p 1 p 2,…, pn,…
Определение. Математическим ожиданием дискретной случайной величины x называется сумма произведений возможных значений xi на соответствующие им вероятности pi. Будем обозначать математическое ожидание как M (x). Тогда можно написать, что математическое ожидание вычисляется по формуле
M (x)= x 1 p 1 +x 2 p 2 +… xn pn +…=  , (2.15)
, (2.15)
если числовой ряд сходится абсолютно. Если числовой ряд (2.15) расходится или сходится условно, то в этом случае математическое ожидание случайной величины x не существует.
 Пример 2.6. Найдем среднее число очков при одном подбрасывании правильного кубика. Используя ряд распределения из примера 2.3
Пример 2.6. Найдем среднее число очков при одном подбрасывании правильного кубика. Используя ряд распределения из примера 2.3
xi 1 2 3 4 5 6
pi 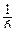
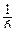
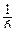
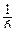
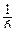
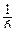
по формуле (2.15) находим математическое ожидание
M (x)=1* 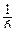 +2*
+2* 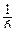 + 3*
+ 3* 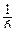 + 4*
+ 4* 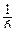 + 5*
+ 5* 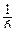 + 6*
+ 6* 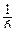 =3,5.
=3,5.
Пример 2.7. Найдем среднее число суммы очков на двух кубиках.
Используя ряд распределения
 η 2 3 4 5 6 7 8 9 10 11 12
η 2 3 4 5 6 7 8 9 10 11 12
pi 
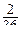


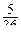



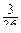

 ,
,
получаем
M(x)=2×  +3×
+3× 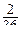 +4×
+4×  +5×
+5×  +6×
+6×  +7×
+7×  +8×
+8× 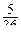 +9×
+9×  +10×
+10×  +11×
+11×  +12×
+12×  =
=  =7.
=7.
Пусть x обозначает непрерывную случайную величину с плотностью вероятности f (x).
Определение. Математическим ожиданием M (x) абсолютно непрерывной случайной величины x называется величина, равная
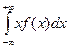 , (2.16)
, (2.16)
если этот несобственный интеграл сходится абсолютно. В противном случае математическое ожидание случайной величины x не существует.
Пример 2.8. Пусть случайная величина x имеет равномерный закон распределения. В этом случае плотность вероятности f (x) имеет вид
 . (2.17)
. (2.17)
Тогда по формуле (2.16) получаем формулу для вычисления математического ожидания равномерно-распределенной случайной величины M(x)=  =
=  +
+  +
+  =
= 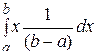 =
=  .
.
Пусть x обозначает дискретную случайную величину с рядом распределения

 xi x 1 x 2 ,…, xn,…
xi x 1 x 2 ,…, xn,…
pi p 1 p 2 ,…, pn,…,
и g (x) – некоторая функция переменной x. Новая случайная величина η = g (ξ) будет дискретной случайной величиной с рядом распределения

g (xi) 
pi p 1 p 2, …, pn …,
причем вероятности этих значений остаются теми же, что и для случайной величины x, а значениями будут числа g (xi). Тогда математическое ожидание случайной величины η = g (ξ)можно вычислить по формуле
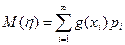 . (2.18)
. (2.18)
Пусть x обозначает случайную величину с плотностью вероятности f (x). Тогда математическое ожидание случайной величины η = g (ξ)можно вычислить по формуле

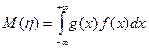 , (2.19)
, (2.19)
если несобственный интеграл сходится абсолютно.
Определение. Математическое ожидание дискретной случайнойвеличины  определяется формулой
определяется формулой
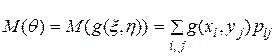 , (2.20)
, (2.20)
если числовой ряд (2.20) сходится абсолютно.