Кроме дискретных существуют непрерывные случайные величины. Примером непрерывной случайной величины является расстояние от точки попадания до центра мишени.
Определение. Случайная величина x называют непрерывной, если ее значения целиком заполняют конечный или бесконечный интервал числовой оси.
Определение. Непрерывная случайная величина x называется абсолютно непрерывной, если существует такая функция f (x), что для любых действительных чисел x функция распределения этой случайной величины F (x) представима в виде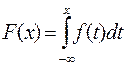 
, (2.7)
т. е. функция распределения F (x) этой случайной величины является интегралом с переменным пределом от f(x) .Функция f (x) называетсяплотностью распределения вероятностей случайной величины x такой, что
.
Рассмотрим пример абсолютно непрерывной случайной величины.
Пример 2.5. Равномерное распределение
Случайная величина ξ распределена равномерно на промежутке [ a,b ], еслиее плотность распределения вероятностей задается равенством
, (2.8)
и имеет график
Построим функцию распределения F (x) этой случайной величины, используя равенство (2.7). При всех x < a по определению f(x) подынтегральная функция f (t)=0. Следовательно, функция распределения F (x)=0.
При всех a £ x < b по определению f (x) подынтегральная функция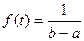 
. Тогда из равенства (2.7) получаем
.
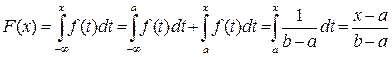При 
по свойству определенного интеграла и определению подынтегральной функции получаем следующее равенство
.
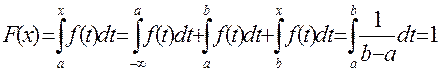Следовательно, функция распределения равномерного закона имеет вид:
. (2.9)
|
Функция распределения и ее свойства
Для функции распределения F (x) случайной величины ξ имеют место следующие свойства:
1) Для всех x выполняются неравенства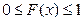 
.
2) Функция распределения случайной величины есть неубывающая функция аргумента x: F (x 1) £ F (x 2), если 
. (2.10)
3) 
, 
.
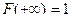4) Функция распределения непрерывна справа F (x+ 0)= F (x).
5) Вероятность попадания случайной величины 
в интервал (a, b ] можно вычислить по формуле
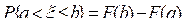. (2.11)
Плотность распределения вероятности и ее свойства
Плотность распределения вероятностей f (x) удовлетворяет следующим свойствам.
1) В точках x непрерывности f (x) имеет место равенство
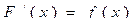. (2.12)
.
2) Для всех x плотность распределения вероятностей неотрицательна, т.е. 
.
3) Вероятность попадания случайной величины в любой интервал [a,b] равна
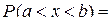
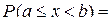
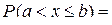
. (2.13)
Это свойство означает, что удаление конечного числа точек из промежутка [ a,b ] не влияет на величину вероятности попадания в этот интервал.
4) Условие нормировки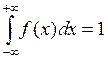 
. (2.14)
График y=f(x) называют кривой распределения. Графически свойство 3 ) означает, что вероятность попадания случайной величины в интервал [ a,b ] численно равна площади S криволинейной трапеции, ограниченной сверху кривой распределения y=f (x), снизу - осью O x, вертикальными прямыми x=a и x=b. Графически свойство 4) означает, что площадь криволинейной трапеции под всей кривой распределения y=f (x) равна 1.
Вопросы для самопроверки
1. Какая величина называется дискретной случайной величиной?
2. Какую случайную величину называют непрерывной?
3. Что такое ряд распределения случайной величины?
4. Сформулируйте определение функции распределения случайной величины и ее свойства.
5. Что такое плотность вероятности случайной величины и ее свойства?