ТЕМА: ДЕФОРМАЦИИ ПРИ Кручении
Деформация кручения имеет место при действии на брус уравновешенной системы пар сил, расположенных в плоскостях, перпендикулярных продольной оси бруса, рис. 1, а.
Брус, работающий на кручение, называют валом. В поперечных сечениях вала, действует только один внутренний силовой фактор – крутящий момент.
Деформации при кручении
Если на боковую поверхность стержня круглого поперечного сечения нанести сетку (рис. 2.15, а) из равноотстоящих окружностей и образующих, а к свободным концам приложить пары сил с моментами Т в плоскостях, перпендикулярных к оси стержня, то при малой деформации (рис. 2.15, б) можно обнаружить:

Рис. 2.15. Схема деформации при кручении
· образующие цилиндра превращаются в винтовые линии большого шага;
· квадраты, образованные сеткой, превращаются в ромбы, т.е. происходит сдвиг поперечных сечений;
· сечения, круглые и плоские до деформации, сохраняют свою форму и после деформации;
· расстояние между поперечными сечениями практически не изменяется;
· происходит поворот одного сечения относительно другого на некоторый угол.
На основании этих наблюдений теория кручения бруса основана на следующих допущениях:
· поперечные сечения бруса, плоские и нормальные к его оси до деформации, остаются плоскими и нормальными к оси и после деформации;
· равноотстоящие поперечные сечения поворачиваются относительно друг друга на равные углы;
· радиусы поперечных сечений в процессе деформации не искривляются;
· в поперечных сечениях возникают только касательные напряжения. Нормальные напряжения малы. Длину бруса можно считать неизменной;
· материал бруса при деформации подчиняется закону Гука при сдвиге:  .
.
В соответствии с этими гипотезами кручение стержня круглого поперечного сечения представляют как результат сдвигов, вызванных взаимным поворотом сечений
 |
Рассмотрим порядок определения величины крутящего момента Mz:
· Вал разбивают на участки, границами которых являются сечения, где приложены скручивающие моменты и сечения, где изменяется диаметр.
· В пределах каждого участка используют метод сечений: разрезают вал поперечным сечением; отбрасывают одну из частей вала (желательно ту, к которой приложено больше скручивающих моментов или моменты, величина которых неизвестна).
· Пользуясь соответствующими правилами, определяют величину крутящих моментов.
I правило: величина крутящего момента Mz в произвольном сечении вала численно равна алгебраической сумме внешних скручивающих моментов, приложенных к оставшейся части вала.
 .
.
II правило (правило знаков): если внешний скручивающий момент представляется направленным по часовой стрелке при взгляде на поперечное сечение со стороны оставшейся части, то его следует взять со знаком «плюс», а если против часовой стрелки, то со знаком «минус» (рис. 2).
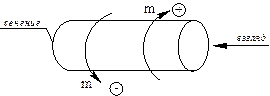
Рис. 2.

Рис. 3.
Порядок построения эпюры «Mz».
· Проводят ось эпюры непосредственно под расчетной схемой (рис. 3, б).
· В пределах каждого участка откладывают значения «Mz» в выбранном масштабе: положительные – вверх, отрицательные – вниз (рис. 3, б).
· Через концы полученных отрезков проводят прямые, параллельные оси эпюры.
· Штрихуют эпюру линиями, перпендикулярными оси эпюры (вала), т.к. каждая линия штриховки имеет определенный физический смысл: в выбранном масштабе она соответствует значению крутящего момента в данном сечении (рис. 3, б).
Указывают на эпюре значения «Mz »в пределах каждого участка.
На большем поле эпюры крутящих моментов один раз сверху от оси указывают знак «плюс», снизу – знак «минус».
Над эпюрой выполняют надпись: Эп. «Mz» (кН×м).
Рассмотрим выше изложенное на примере.
Определим величину крутящих моментов в поперечных сечениях вала, представленного на рис. 3, а.
· Разбиваем вал на три участка.
· Определяем крутящие моменты в поперечных сечениях участков вала:
М1z = -2m; М2z = -2m + 3m = m;
М3z = -2m + 3m + 5m = 6m.
· В данном примере мы отбрасываем во всех случаях левую часть вала, т. к. к ней приложен неизвестный реактивный момент (реакция заделки) (рис. 3, а).
Правила контроля правильности построения эпюры «Мz».
1. В пределах каждого участка эпюра «Мz». изображается прямой, параллельной оси эпюры.
2. В сечениях вала, в которых приложены внешние скручивающие моменты на эпюре, имеются скачки, величина которых соответствует величине приложенного скручивающего момента.
Например: в сечении, где приложен момент 3m, величина скачка равна 3m (2m + m).