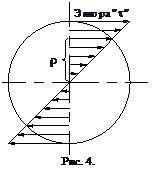
Крутящему моменту соответствуют касательные напряжения t, которые распределяются по линейному закону вдоль диаметра, рис. 4. Величина касательных напряжений в любой точке поперечного сечения может быть определена по формуле:
, (1)
где Mz – крутящий момент;
Ir – полярный момент инерции.
Для круглого сечения полярный момент инерции равен:
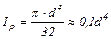, (2)
где d – диаметр круглого сечения;
ρ – расстояние от центра круга (полюса) до точки, в которой определяется напряжение.
Для кольцевого сечения (рис. 6):
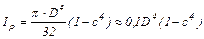. (3)
Из формулы (1) следует, что касательное напряжение в центре сечения равно нулю, а максимальные по величине напряжения действуют в точках контура сечения (так называемые «опасные точки»), т. е. при 
. Величина этих напряжений может быть определена по формуле:
, (4)
где Wr – полярный момент сопротивления.
| 
|
| Рис. 5. | Рис. 6. |
Для круглого сечения:
. (5)
Для кольцевого сечения:
, (6)
где D – внешний диаметр кольца; с – отношение диаметров: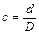 
.
Направление касательного напряжения в каждой точке сечения перпендикулярно радиусу (рис. 5).
Выражение крутящего момента через напряжения:
, (7)
отражает его физический смысл: крутящий момент – есть момент результирующий пары внутренних касательных сил упругости, действующих в поперечном сечении вала.
Расчет на прочность
Прочность бруса, работающего на кручение, считается обеспеченной, если наибольшие касательные напряжения, возникающие в его опасном сечении, не превышают величины допускаемого напряжения.
Для вала постоянного диаметра опасным является участок, в котором действует наибольший крутящий момент. Для вала, представленного на рис. 3, опасным является третий участок.
Для ступенчатого вала, опасным считают участок вала, в поперечных сечениях которого действуют наибольшие по величине касательные напряжения.
Условие прочности при кручении имеет вид:
, (8)
где tmax – максимальное напряжение в опасном сечении вала;
Mz – крутящий момент;
Wр – полярный момент сопротивления поперечного сечения вала;
[t] – допускаемое касательное напряжение; для пластичных материалов принимают равным [t] » (0,55 ¸ 0,60) [s].
Различают три вида расчетов на прочность: проверочный, проектный и определение допускаемой нагрузки.
Проверочный расчет
Осуществляется по условию (8). Расчет производится с целью оценки прочности вала под действием заданной нагрузки.
Порядок расчета
• Разбивают вал на участки.
• Определяют величину крутящих моментов в поперечных сечениях участков вала и строят их эпюру.
• Определяют полярные моменты сопротивления поперечных сечений вала по формулам (5) или (6) в зависимости от формы сечения.
• Определяют максимальные касательные напряжения в поперечных сечениях на каждом участке по формуле (4) и строях их эпюру.
• Делают вывод о прочности, согласно условию (8), то есть сравнивают величину наибольшего касательного напряжения tmax с величиной допускаемого напряжения [t]. Прочность вала обеспечивается, если максимальное касательное напряжение, возникающее в опасном сечении вала, не превышает величины допускаемого напряжения. Допускается перенапряжение в пределах 5%.
Проектный расчет
Осуществляется по условию:
(9)
где Mz = çMzçmax, значение его берем из эпюры «Mz»;
[t] –допускаемое напряжение;
Wr – полярный момент сопротивления.
Порядок расчета
• Разбивают вал на участки.
• Определяют величину крутящих моментов в поперечных сечениях участков вала и строят их эпюру.
• Выясняют опасные участки вала, это участки, в поперечных сечениях которых действуют наибольшие по абсолютной величине крутящие моменты.
• Определяют требуемые моменты сопротивления поперечных сечений вала по формуле (9).
• Определяют диаметры поперечных сечений вала.
Для круглого сечения по формуле:
. (10)
Для кольцевого сечения:
, (11)
где D – наружный диаметр кольца;
;
d – внутренний диаметр кольца.
Полученное значение диаметра следует округлить до ближайшего большого четного числа или числа, оканчивающегося на 5.