Операционный анализ сетей СМО

Тема: Сети СМО

План лекции:

1. Сети СМО.

2. Операционный анализ сетей СМО.

3. Анализ узких мест в сети.

Сети СМО

Существуют системы со сложнейшей структурой – сети, каждым узлом которых являются отдельные СМО. С помощью сетей СМО моделируют много типов транспортных, технологических и вычислительных систем, процессы предоставления медицинской помощи, обслуживания пассажиров и др. Особенный вклад в развитие математических методов в теории сетей СМО в 70-х годах ХХ столетия внесли специалисты, которые занимались моделированием вычислительных систем.

Анализ сетей СМО является более сложным, чем анализ отдельных СМО. Получить результаты в замкнутом виде можно лишь для сетей с количеством узлов не больше трёх. В случаях большего количества узлов используются численные методы, что значительно усложняет расчеты. Кроме того, анализ сетей СМО возможен лишь в тех случаях, когда вероятностные процессы в сетях являются эргодическими, независимыми и протекают по известным законам распределения вероятностей.

Все нужные для расчетов величины также должны быть определены количественно. Однако, на практике сделать это не всегда удаётся.

В общем случае сеть СМО можно изобразить в виде графа, вершинами которого являются одноканальные или многоканальные СМО (дуги определяют потоки передвижения требований).

Простейшая сеть образуется путем последовательного соединения нескольких СМО (рис.1).

Рис.1. Простейшая разомкнутая сеть СМО

Такую сеть ещё называют многофазовой СМО. Различают замкнутые и разомкнутые сети. Для замкнутой стохастической сети не существует внешних источников требований, т.е. в ней всегда находится одинаковое количество требований. Замкнутая сеть изолирована от внешней среды. В разомкнутой сети (рис.1) существуют источники и стоки требований.

Простейшая замкнутая сеть (рис.2) имеет только два узла. Первый узел содержит М устройств для обслуживания, а второй – 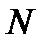. Такая сеть является моделью СМО с отказами и обновлением. Устройства для обслуживания М могут выходить из строя и обновляться с заданными интенсивностями в случайные моменты времени. В этой сети постоянно находится М требований, которые появляются в случае отказа устройств обслуживания. Если устройство выходит из строя, то к бригаде с 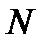ремонтниками поступает требование на его ремонт, после завершения которого устройство возобновляет свою работу.

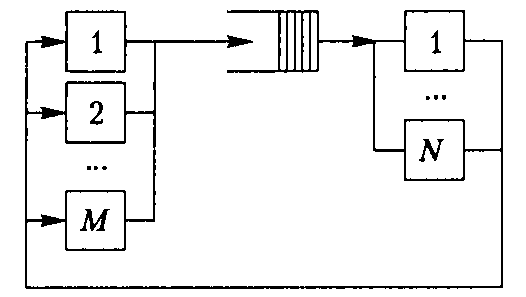
Рис.2. Простейшая замкнутая сеть СМО

На рис.3 это обозначено обратной связью от 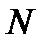устройств. Данная сеть может использоваться и для моделирования компьютерной системы, которая работает в режиме «запрос – ответ». В такой системе пользователь не посылает новый запрос в систему до тех пор, пока не получит ответ на предыдущий запрос. Запросы обрабатывают любые из 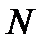компьютеров. Примерами таких систем могут быть автоматизированные системы продажи билетов, системы передачи транзакций от кассиров в банке и др.

Сеть СМО (рис.3) содержит К узлов, а также 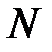требований. Каждый узел может содержать один или несколько одинаковых устройств для обслуживания. С вероятностью (или частотой) 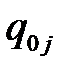требования поступают в любой узел сети СМО, а с вероятностью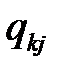 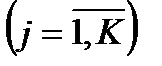требование оставляет узел 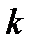и направляется в узел 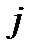. Таким образом, каждое требование в процессе обслуживания в сети проходит несколько узлов. Внешняя среда обозначается как узел 0 сети. Если сеть замкнута, то требования от выхода поступают на вход (рис.3, пунктирная линия) и количество требований 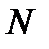в сети не изменяется.

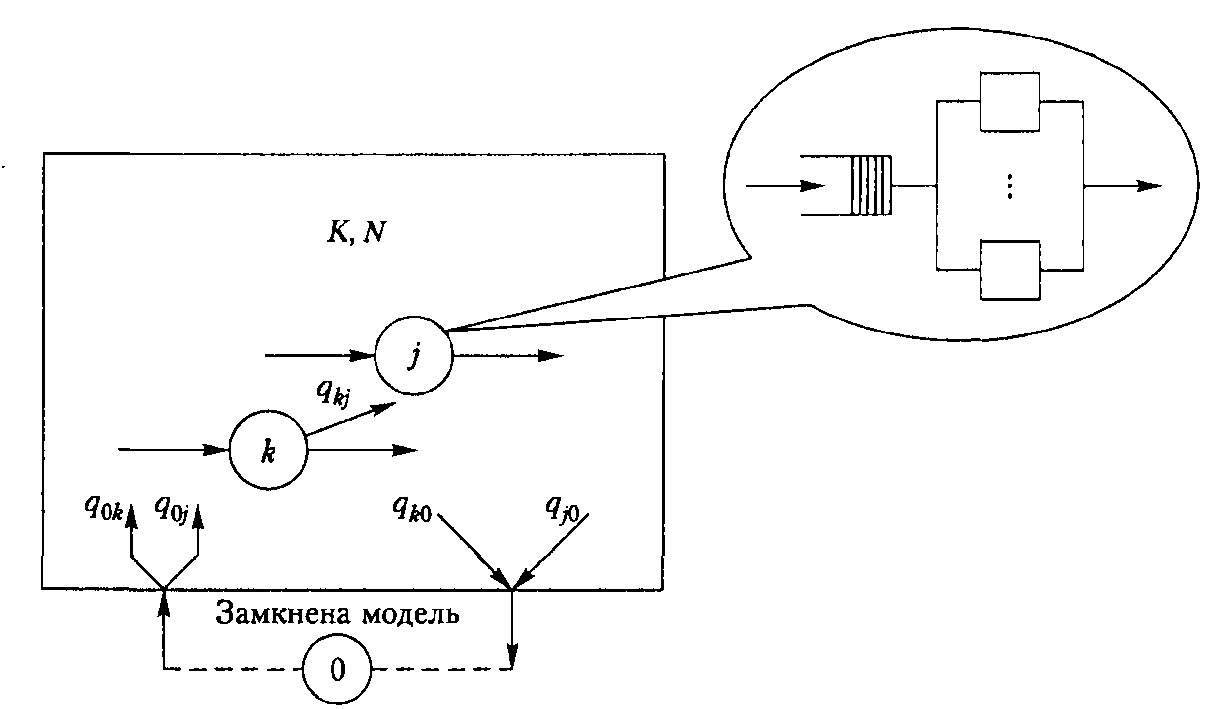
Рис.3.Схематическое изображение сети СМО

ри постоянном режиме сети для потоков требований справедливы законы о суммарных потоках (рис.4):

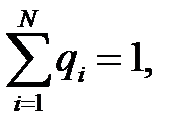
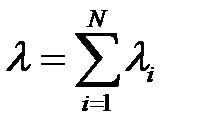
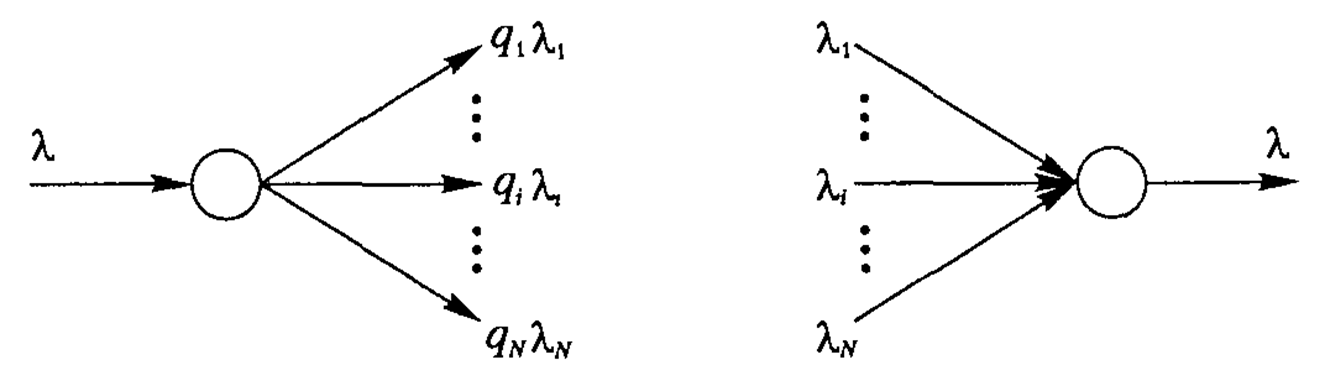
Рис.4.Разветвление и суммирование потоков требований сети.

Для расчетов сетей СМО используется теория стохастических сетей, которая основывается на марковских или полумарковских процессах, но большинство результатов получено только для экспоненциальных законов распределения поступления и обслуживания требований.

Операционный анализ сетей СМО

Операционный анализ впервые был предложен для вычисления показателей работы компьютеров и компьютерных систем. Он предоставляет математический аппарат для анализа технических и экономических систем многих типов и позволяет легко определить показатели их работы.

Операционный анализ, в отличие от ТМО базируется на моделировании логики работы системы. Это даёт возможность установить простые зависимости между параметрами и показателями работы системы, не абстрагируясь от процессов её функционирования.

Операционный анализстохастических сетей базируется на таких положениях:

- все допущения относительно свойств входных и выходных переменных системы можно проверить путём измерений параметров функционирования реальной системы или её модели в течение конечного промежутка времени;

- в системе должен существовать баланс потоков требований: количество требований, которые покинули систему на протяжении некоторого периода наблюдения, равно количеству требований, которые поступили в систему за этот же период;

- устройства для обслуживания должны быть однородными, поступления требований от одного узла к другому не должны зависеть от длины очередей в узлах и времени окончания обслуживания устройствами.

Основное задание анализа стохастических сетей заключается в определении таких показателей, как среднее время пребывания требований в отдельных узлах сетей, среднее время загрузки устройств в узлах, средние длины очередей до узлов и т.д.

Большинство результатов операционного анализа касается замкнутых сетей, когда требования, которые оставляют сеть, снова возвращаются в неё. Модели замкнутых сетей можно применять для исследования систем, которые работают с перегрузкой, т.е. в которых всегда есть очередь требований.

Операционные переменные

Введем операционные переменные, значения которых можно получить путем непосредственного измерения параметров реальной системы или в процессе имитационного моделирования:

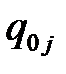– вероятность (частота) поступления внешних требований в любой узел сети, 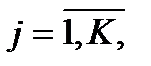де К – общее количество узлов;

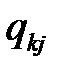– вероятность поступления требований от узла 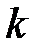до узла .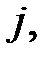

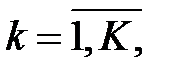
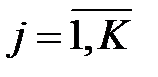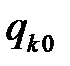– вероятность того, что после окончания обслуживания в узле 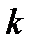требования покидают сеть;

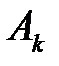– количество требований, которые поступили в узел ,

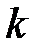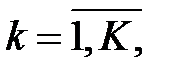
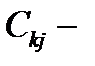количество требований, которые покинули узел 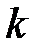и поступили в узел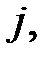

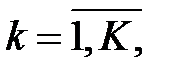
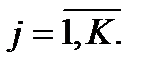
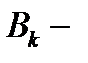общее время обслуживания требований в узле ,

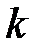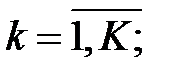
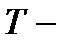общее время наблюдения за системой или время моделирования.

Внешнюю среду сети обозначим как вершину с номером 0. Тогда параметры 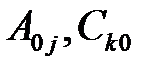приобретают соответственно значения количества требований, которые поступили в узел 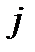извне, и требований, которые покинули узел 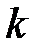и сеть.

Узел считается занятым, если в нём есть хотя бы одно требование. Введем дополнительные обозначения:

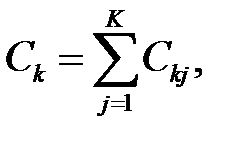
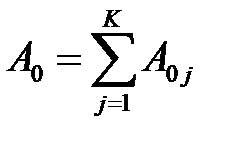
Введенные переменные называются основными операционными переменными. Путем простейших операций над ними получают операционные переменные, которые выводятся (например, интенсивность поступления требований в узел 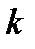определяется как 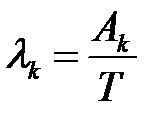). Среди этих операционных переменных чаще используют следующие:

- коэффициент использования узла 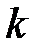: 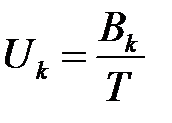; (1)

- среднее время обслуживания в узле 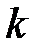: 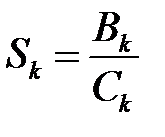; (2)

- интенсивность выходного потока требований от узла 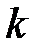: : 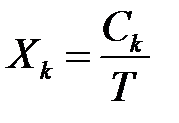(3)

- относительную частоту перемещения требований между узлам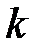и и :

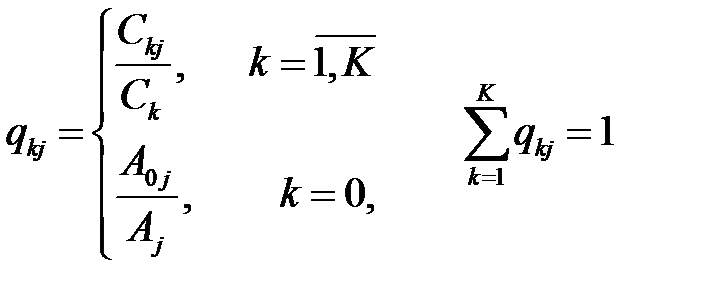
Используя выражения (1)–(3), получим: 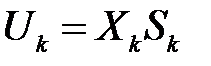. (4)

Выражение (4) – это закон использования узла, который выполняется при условии, что 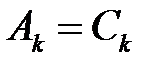на протяжении всего периода наблюдения Т (в этом случае ).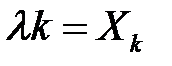