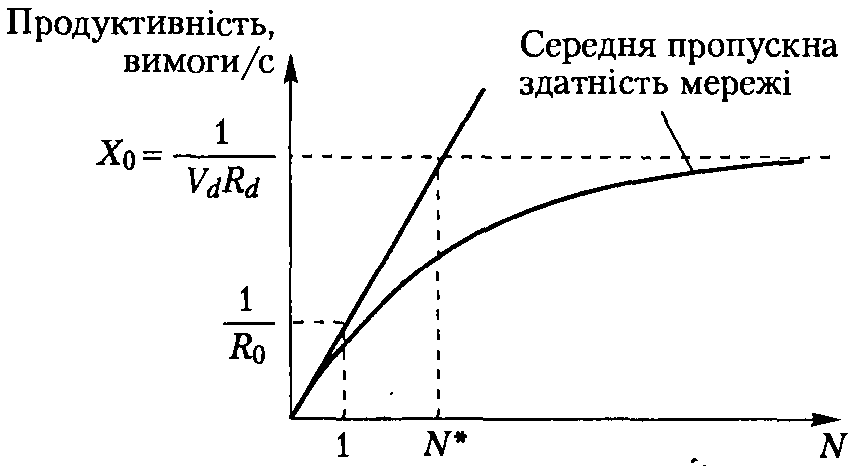
Рис. 8. График зависимости продуктивности сети от количества требований
Для замкнутой сети с количеством устройств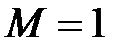 
время пребывания требования в сети 
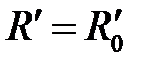. В случае увеличения 
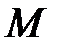поток требований от сети будет увеличиваться, однако, не будет превышать 
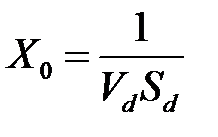. Таким образом, 
, 
.
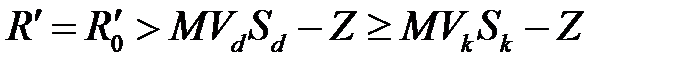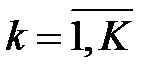Итак, в случае увеличения 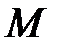среднее время пребывания требования в сети имеет асимптоту 
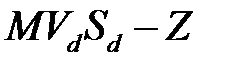. На рис. 9 показана зависимость среднего времени пребывания требования в замкнутой сети от количества устройств .
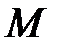Рис. 9. Зависимость времени пребывания требований от количества устройств в замкнутой сети
Пример. Вычислим характеристики замкнутой сети, показанной на рис. 10, где приведены значения операционных переменных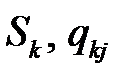 
и 
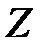2.
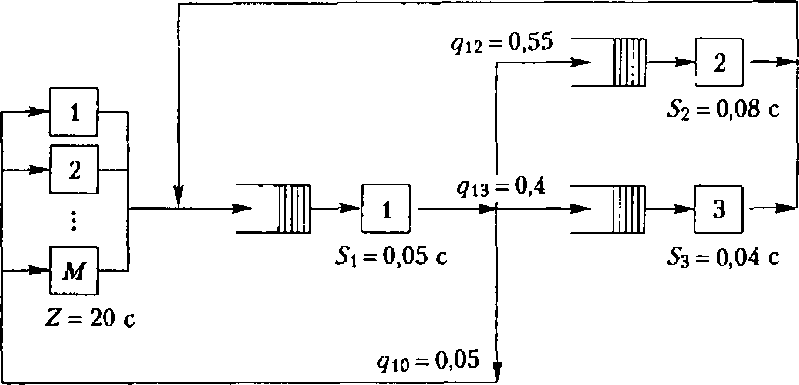
Рис. 10. Пример сети СМО
Запишем уравнения баланса потоков требований для коэффициентов посещения этой сети:
,
,
.
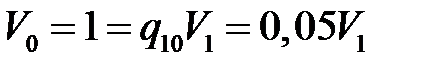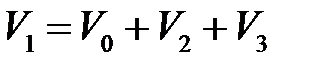
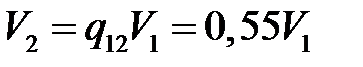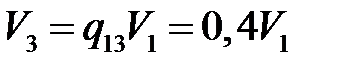Решив эту систему уравнений, получим: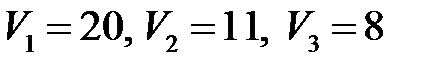 
.
Вычислим значения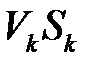 
для каждого из узлов сети:
.
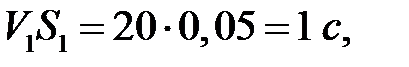
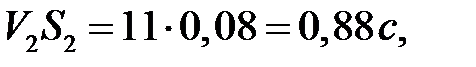
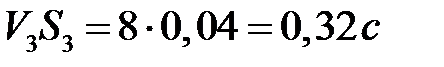Таким образом, минимальное среднее время пребывания одного требования в сети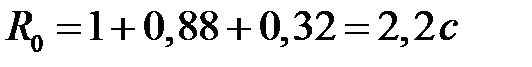 
. Поскольку 
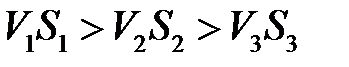, то потенциальным узким местом в сети является первый узел.
С помощью метода операционного анализа можно найти ответ, например, на такие вопросы.
1. Какое среднее количество устройств М для обслуживания взаимодействует с сетью в течение всего времени наблюдения? Пусть с помощью измерений определено, что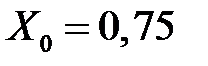 
треб/с, а среднее время пребывания требования в сети равно 
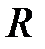= 5,2 с.
По формуле (13) имеем:
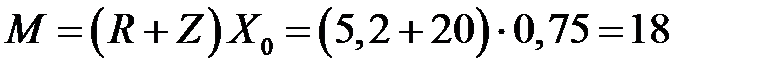устройств.
2. Можно ли обеспечить среднее время пребывания требований в сети, которое равно 8с, если количество устройств для обслуживания равно 30? Чему должно быть равно максимальное среднее время обслуживания требования в первом узле, чтобы это стало возможным?
По формуле (13) имеем: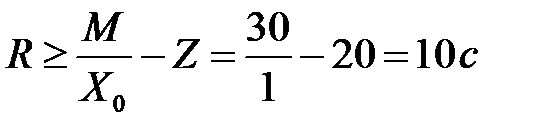 
.
Таким образом, в случае взаимодействия с сетью 30 устройств для обслуживания среднее время пребывания требования в ней составит более 10 с.
Обозначим через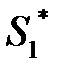 
допустимое среднее время обслуживания требования. Тогда можно записать:
, 
.
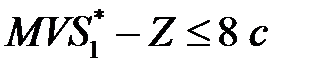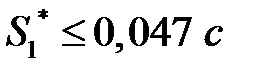Т.е. максимально возможное среднее время обслуживания требования в узле 1 составляет 0,047 с.
Выводы:
♦ ТМО определяет зависимость между параметрами потоков требований, количеством устройств обслуживания и их продуктивностью, а также между режимами функционирования СМО и её эффективностью.
♦ Основные теоретические результаты ТМО получены для систем, в которых процессы поступления и обслуживания требований являются марковскими и полумарковскими.
♦ Замкнутая сеть СМО — это изолированная от внешней среды сеть, для которой не существует внешних источников и стоков требований.
♦ Разомкнутая сеть СМО — это сеть, в которой требования, которые обрабатываются устройствами обслуживания, могут поступать из внешней среды.
♦ Операционный анализ является методом исследования сетей СМО, в основе которого лежат операционные переменные. Основные результаты операционного анализа формируются в виде соотношений между операционными переменными.
♦ Условия функционирования сети СМО определяет гипотеза о балансе потоков в сети: количество требований, которые поступили в некоторый узел в течение продолжительного периода времени, равно количеству требований, которые покинули этот узел.