Для упругих волн уравнение волны представляет собой выражение, которое задает смещение 
колеблющейся частицы как функцию координат равновесного положения частицы и времени. Пусть волна распространяется в направлении оси X, тогда
.
Эта функция должна быть периодической как относительно времени t, так и относительно координаты 
. Периодичность во времени вытекает из того, что описывает колебания частицы с координатой . Периодичность по координатам следует из того, что точки, отстоящие друг от друга на расстоянии, равном длине волны, колеблются одинаковым образом.
|
Найдем вид функции в случае плоской волны, предполагая, что колебания носят гармонический характер. Пусть колебания точек, лежащих в плоскости 
, имеют вид:
.
Найдем вид колебаний точек в плоскости, соответствующей произвольному значению 
. Для того, чтобы пройти путь от плоскости до этой плоскости, волне требуется время 
(
– скорость распространения волны) (рис. 8.3). Следовательно, колебания частиц, лежащих в плоскости , будут отставать по времени на 
от колебаний частиц в плоскости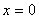 
, то есть будут иметь вид:
| (8.1) |
где 
– амплитуда волны. Начальная фаза волны 
определяется выбором начала отсчета и 
. Зависимость фазы рассматриваемой волны и от времени, и от пространственных координат означает, что каждое данное значение фазы распространяется в пространстве.
Волна, распространяющаяся в противоположном направлении, описывается уравнением:
.
В физике обычно используют обозначение 
. Величину 
называют волновым числом. Используя это обозначение, уравнение плоской волны, распространяющейся в положительном направлении оси 
, можно записать в виде:
 .
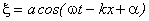| (8.2) |
Это уравнение монохроматической волны, распространяющейся со скоростью в положительном направлении оси X. Различные точки волны в момент времени имеют разные смещения. Но ряд точек, отстоящих на расстояние 
одна от другой, в любой момент времени смещены одинаково (так как аргументы косинусов в уравнении (8.2) отличаются на 
и, следовательно, их значения равны). Это расстояние и есть длина волны 
. Она равна пути, который проходит волна за один период колебаний частиц среды.
Скорость смещения элементов среды равна производной от смещения частицы по времени:
.
Таким образом, скорость смещения элементов среды меняется по тому же закону, что и само смещение, но со сдвигом по фазе на 
: скорость достигает максимума, когда смещение падает до нуля. Введенная выше скорость описывает распространение только бесконечной монохроматической волны. Она определяет скорость перемещения ее фазы и называется фазовой скоростью.
Все приведенные рассуждения относятся к распространению волн в непоглощающей среде, то есть в среде, в которой механическая энергия не переходит в другие виды энергии.
Замечание
При выводе соотношения 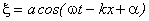мы полагали, что амплитуда колебаний не зависит от координаты . Для плоских волн это справедливо, когда энергия волны не поглощается средой. При распространении же в поглощающей энергию среде наблюдается затухание волны, причем, как показывает опыт, в однородной среде затухание происходит по экспоненциальному закону:
и, соответственно, уравнение плоской волны имеет следующий вид:
.