Обработка экспериментальных данных

1. Внимательно ознакомиться с описанием лабораторной установки.

2. Изучить правила техники безопасности при выполнении лабораторной работы.

3. Изучить работу электрической схемы электронного расходомера топлива (рис. 2).

4. Произвести пятьдесят замеров расхода топлива. Во время опыта замерить объем топлива между верхним и нижним уровнями в мерном сосуде.

5. Определить относительную ошибку измерения расхода.

6. Построить гистограмму распределения абсолютной ошибки рас

 

Обработка экспериментальных данных

Результаты замеров свести в таблицу.

 

п/п	Ti	Qi	ΔQi	ΔQi2	Примечание
….
….

 

Относительная ошибка измерения расхода

где Zp - квантиль нормального распределения (Z0,9 = 1,64; Z0.95 = 1.96; Z0.997 = 3). Средний расход, см3 /с,

 

 

Среднее квадратическое отклонение расхода, см3 /с,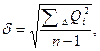

 

 

где

 

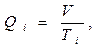Текущий расход, см3 /с,

 

где Ti- время истечения топлива, с; V - объем топлива в мерном сосуде, см3.

Шаг гистограммы определяется по формуле Стеджерса, см3/с, размах экспериментальных данных, см3 /с.

 

Содержание отчета

 

1. Цель работы.

2. Краткие теоретические сведения.

3. Принципиальная электрическая схема электронного расходомера топлива (рис. 2).

4. Экспериментальные данные.

5. Относительная ошибка измерения расхода при различных уров­нях доверительной вероятности.

6. Гистограмма распределения ошибки расхода.

 

Вопросы для самопроверки

 

1. На какие характеристики автомобиля влияет расход топлива?

2. Какие диагностические признаки неисправностей системы питания двигателя автомобиля вам известны?

3. Какие типы расходомеров используются при замерах расхода топлива автомобильным двигателем?

4. На каких режимах работы автомобильного двигателя произво­дится измерение расхода топлива?

5. Каковы основные источники погрешностей и определении расхо­да топлива при неавтоматизированном способе измерения?

6. Какие преимущества дает автоматизация измерения расхода топлива?

7.. Как определяется относительная ошибка измерения расхода?

 

Библиографический список

 

1. Аринин И.Н. Техническая диагностика на предприятиях автомобильного транспорта. Ярославль: Верхневолжское изд-во, 1974. 143 с.

2. Райков И.Л. Испытание двигателей внутреннего сгорания. М.: Высш.ш. 1975. 320 с.

3. З.Яковлев Л.Г. Приборы контроля работы силовых устано­вок. М.: Машиностроение. 1969. 300с.

 

Лабораторная работа №6

Параметрические чувствительные элементы

 

Цель работы: Изучение принципов работы параметрических датчиков. Снятие экспериментальных характеристик датчиков (реостатного, ин­дуктивного, емкостного).

 

Общие указания

 

Электрические чувствительные элементы находят широкое примене­ние в системах автоматизация производственных процессов на авто­мобильном транспорте. Наиболее характерными областями их примене­ния являются: диагностика технического состояния узлов и агрега­тов автомобиля; измерение газового состава производственных поме­щений, стоянок автомобильного транспорта, городского воздушного бассейна; контроль за состоянием и работой отдельных систем, меха­низмов, агрегатов я автомобиля в целом и т.д.

Электрические чувствительные элементы подразделяются на две группы: параметрические и генераторные. Параметрические чувстви­тельные элементы преобразуют входную физическую величину X в изме­нение параметра электрической цепи (сопротивление R, емкость С, индуктивность L и взаимоиидуктивность М). Для функционирования параметрических чувствительных элементов необходим источник пита­ния.

Реостатные и потенциометрические чувствительные элементы приме­няются в основном для измерения перемещений и сил, под действием которых изменяется сопротивление элемента.

Омическое сопротивление проводника в Ом определяется выражением R = pl/S, где р - удельное сопротивление материала провод­ника, Ом.м; l - общая длина проводника, м; S - площадь попереч­ного сечения, м2.

Поскольку р, l, S зависят от деформаций, механических напря­жений, усилий, давлений, перемещений и других параметров, то R яв­ляется сложной функцией этих параметров. Для измерения какого-либо одного из них, например усилия, необходимо, чтобы сопротивление было функцией только усилия при постоянстве всех остальных.

Наибольшее распространение получили проволочные чувствительные элементы, схема и конструкция которых приведены на рис. 1, а. На неподвижный каркас 1 плотно, виток к витку, наматывают изолирован­ный провод, который образует обмотку 2 с сопротивлением R. Обмот­ка включается в цепь постоянного напряжения U. На обмотке очища­ется от изоляции "контактная дорожка", по которой перемещается щетка 3, жестко закрепленная в щеткодержателе 4.

Каркас изготавливается из пресс-порошка, эбонита, анодированно­го алюминия и других изоляционных материалов. Наиболее распростра­ненными материалами провода являются манганит, константен, а так­же сплавы на базе благородных металлов. Диаметр провода изменяет­ся в пределах 0,03 - 0,1 мм для прецизионных реостатов и потенци­ометров, а в грубых реостатах достигает 0,3 мм.

Статистической характеристикой реостатного чувствительного эле­мента является зависимость R_вых=f(x) а потенциометрического -зависимость U_вых=f(x) где X - перемещение. Ступенчатый вид ха­рактеристики (рис. 1, б, в) объясняется тем, что при движении щет­ки вдоль обмотки в момент перехода от одного витка к другому со­противление или напряжение изменяется скачком. Так, для линейного реостата максимальная величина витковой погрешности определяется выражением ΔR=0.5r=0.5R/w, где R - сопротивление реостата; r - сопротивление одного витка; w - число витков.

Для нелинейного потенциометра витковая погрешность вычисляется по наиболее крутому участку характеристики: ΔU=U1/2w, где

U1 - приращение выходного напряжения на наиболее крутом участке характеристики; w - число витков на этом участке.

Нелинейные характеристики обычно получают путем профилирования каркаса по определенному закону или шунтированием отдельных участков линейного потенциометра.

Емкостные чувствительные элементы нашли применение для измере­ния перемещений (линейных и угловых), усилий, давлений, уровня, расходов, крутящих моментов, температуры и других физических ве­личин. Принцип действия емкостных чувствительных элементов состоит в том, что замеряемая величина может быть связана с одним из параметров, определяющих емкость конденсатора, а именно, диэлект­рической постоянной среды, эффективной площадью электродов, рас­стоянием (зазором) между электродами, диэлектрическими потерями, а также электростатической силой напряжения электродов.

Емкость плоского конденсатора (рис. 2, а) равна C=εS/δ, где С - емкость, Ф; ε- диэлектрическая проницаемость среды между электродами конденсатора, равная ε=ε₀*ε_r;

ε₀= 8,85*10^-12, Ф/м - аб­солютная диэлектрическая проницаемость вакуума; ε_r - относитель­ная диэлектрическая проницаемость среды между электродами (для воздуха εr = 1; δ - расстояние между электродами, м.

Емкость вращающегося конденсатора (рис. 2, б) равна

 

 

где α - угол поворота электродов конденсатора, рад; S_max - мак­симальная площадь электродов, м²; C_max - максимальная емкость, Ф.

Преимуществами емкостных чувствительных элементов являются вы­сокая чувствительность, малые габаритные размеры и простота кон­струкции. Индуктивные чувствительные элементы нашли широкое при­менение для измерения перемещений, усилий, давлений, скоростей, крутящих моментов и других физических величин, а также в качестве источника ультразвуковых колебаний.

Принцип их действия основав на том, что индуктивность и полное сопротивление зависят от параметров магнитной цепи. Если связать измеряемую величину (например, усилие или угловое перемещение) с одним из параметров магнитной цепи, то по изменению индуктивности или сопротивления можно судить об этой величине.

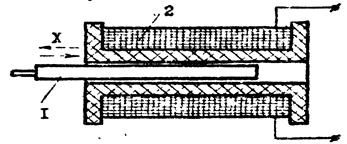
Для измерения больших перемещений (до десятков миллиметров) используется индуктивный датчик, показанный на рис. 3. На сердеч­ник 1, расположенный в обмотке 2, воздействует измеряемая неэлек­трическая величина х, вызывающая его перемещение. Вследствие этого изменяется полное сопротивление катушки, в следовательно, сигнал на входе элемента.

Полное сопротивление обмотки индуктивного датчика равно

 

где R - активная составляющая сопротивления, Ом; v - угловая электрического поля, рад/с; L - индуктивность, Гн.

 

Рис.1. Реостатный потенциометрический чувствительный элемент: а – конструкция; б – линейная характеристика; в – нелинейная характеристика.

 

 

Рис.2. Ёмкостный чувствительный элемент: а – для линейных перемещений; б – для угловых перемещений.

 

 

Рис.3. Индуктивный чувствительный элемент

Индуктивность обмотки датчика определяется выражением

Где ω - число витков обмотки датчика; Ф - магнитный поток, Вб;

(I - ток, протекающий по обмотке датчика, А; Rст - магнитное со­противление сердечника, Гн; Rв - магнитное сопротивление воз­душного зазора, Гн-1.

Поскольку при перемещении сердечника внутри обмотки индуктив­вого датчика происходит изменение соотношения между Rст и Rв, до которым замыкается магнитный поток, происходит изменение ин­дуктивности L, а следовательно, и полное сопротивление датчика Z.