Задача 2. Влияние автоколебательных вибрационный помех на устойчивость и качество процесса управлениям

Наряду со специальным использованием автоколебаний, изложенным в задаче 1, могут быть случаи их вредного влияния вплоть до нарушения устойчивости процесса управления. Это влияние совершенно аналогично действию внешних вибрационных помех (лекция 25).

Обратимся к той же задаче учета упругих вибраций корпуса самолета в полете, как и при исследованиявибрационной помехоустойчивости в предыдущей лекции. Там эти вибрации считались поступающими на гироскоп извне. Строго же говоря, они имеют место внутрисистем мы, как показано на рис. 6.18, а, где автопилот и самолет составляют прежний контур управления, в котором рассматривается движение самолета как твердоготела. Но теперь параллельно ему подключен еще контурупругих колебаний корпуса с уравнением

где J1 — угол отклонения при изгибе оси самолета в точке установки гироскопа. Изгибные вибрации при таком рассмотрении являются автоколебательными.

Чтобы определить коэффициент усиления kн нелиней­ности F(x) автопилота в процессе управления, нужно найти сначала амплитуду симметричных изгибных колебаний а с.

Рис. 6.18.

Поскольку они не проходят через звено «само­лет как твердое тело», то для определения а с рассчиты­ваются автоколебания в отдельном контуре (рис. 6.18, б). Затем полученное значение а с используется при опреде­лении kн, после чего система самолет — автопилот исследуется как линейная с учетом выражения kн че­рез другие параметры системы (см. пример, приводив­шийся выше). Заметим, что поскольку коэффициент демпфирования в уравнении (6.44) мал, то частота автоколебаний будет близка к значению с в уравнении (6.44). Оно и давало возможность рассматривать в предыдущей лекции прохождение автоколебаний через автопилот как прохождение вынужденных колебаний с заданной извне частотой.

 

 

ЛЕКЦИЯ 27 Колебательные переходные процессы.

План.

1. Определение качества колебательных переходных процессов.

2. Диаграммы качества.

3. Пример построения диаграмм качества.

4. Смещённая частотная характеристика.

 

Рассмотрим определение качества колебательных переходных процессов в нелинейных системах (рис. 6.19). Эти процессы могут быть затухающими до нуля или до амплитуды автоколебаний и расходящимися изнутри до амплитуды автоколебаний, или же расходящимися неограниченно в случае неустойчивости.

Будем рассматривать их как собственные колебания при отсутствии внешних воздействий во время самого процесса. Уравнение нелинейной системы (рис. 6.20), как известно, имеет вид

В линейных системах синусоидальные переходные колебания имели вид

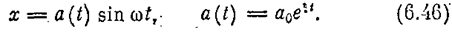
Для линейной системы высокого порядка такое решение является приближенным в том смысле, что оно соответствует одной паре комплексных корней характеристического уравнения системы. Чтобы это решение отвечало основной части переходного процесса, эта пара корней должна быть ближайшей к мнимой оси.

В нелинейных системах, удовлетворяющих свойству фильтра (см. лекцию 12), будем считать переходные колеба­ния близкими к синусоидальным (6.46), полагая, однако, что показатель затухания x и частота w медленно изме­няются с изменением амплитуды колебаний а в ходе процесса. Сама амплитуда a (t) может меняться быстро вплоть до затухания за один-два периода.

 

Рис.6.19.

 

 

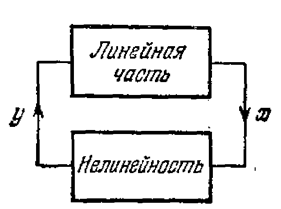
Рис. 6.20.

Тогда решение вместо (6.46) надо искать в виде

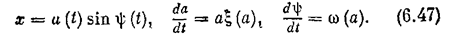
Как частный случай отсюда при x = const и w = const Получается формула (6.46) для линейных систем,

При x <. 0 колебания затухают, при x > 0 — расхо­дятся.

Гармоническая линеаризация нелинейности здесь изменится, поскольку из (6.47) имеем

Отсюда

В связи с этим первая гармоника колебаний на выходе нелинейности вместо прежнего (4.10) получит выражение

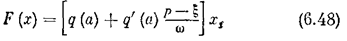
где коэффициенты гармонической линеаризации q и q' определяются, как и раньше, формулами (4.11). Поэтому здесь для конкретных нелинейностей можно пользоваться результатами, полученными в лекции 13, 14.

Затухающие или расходящиеся колебания в линейной системе соответствуют комплексным корням характери­стического уравнения. Следовательно, для их определе­ния нужно в характеристическое уравнение гармонически линеаризованной системы (вытекающее из (6.45) и (6.48))

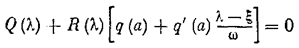
подставлять l = x+jw, полагая, что это соответствует ближайшей к мнимой оси паре комплексных корней. В ре­зультате получим

В это комплексное уравнение входят неизвестные величины x, w, а. Следовательно, из этого уравнения можно найти две из них как функцию третьей:

Этого достаточно, чтобы затем по формулам (6.47) при­близительно определить и кривую переходных колеба­ний х (t).

В большинстве случаев при проектировании системы автоматического управления и регулирования не требуется вычерчивать кривую переходного процесса. Нужна лишь оценка быстроты затухания и частоты колебаний, т. е. для оценки качества переходного колебательного процесса в большинстве случаев можно ограничиться определением зависимостей x(a) и w(а) из уравнения (6.49).

Один из способов определения этих зависимостей со­стоит в следующем (другие способы описаны в [22]). Выделив в уравнении (6.49) вещественную и мнимую части, получим два уравнения

из которых и определяются зависимости (6.50).

Если нужно выбирать какой-либо параметр системы, например коэффициент усиления линейной части kл, так,

Рис. 6.21.

чтобы x и w удовлетворяли заданным требованиям, то можно пользоваться так на­зываемыми диаграммами качества. Они строятся следующим образом. Пусть в ка­кой-либо системе мы определили зависимость амплитуды автоколебаний а п от пара­метра kл, как показанонарис. 6.21. Здесь по параметру kл выделена область устойчивости равновесного состоя­ния. В автоколебательном ре­жиме имеем а = а п = const, т. е. x = 0. Ниже линииАВ (рис. 6.21) колебания расходятся. Следовательно, там x > 0. Выше линии АВ колебания затухают и, значит, там x < 0. На самой линии АВ имеем x = 0.

Если на основании уравнений (6.51) провестилинии равных значений x, то получится диаграмма, изображен­ная на рис. 6.22. Взяв некоторое значение kл = k1 в об­ласти устойчивости равновесия, получим (идя по верти­кали) зависимость x(а), показанную на рис. 6.23, а. Для значения же kл = k2 в области автоколебаний (рис. 6.22) зависимость x(а) будет иметь инойвид (рис, 6.23, б). Эти графики дают представление о качестве

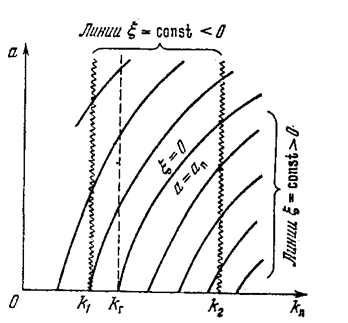
Рис.6.22.

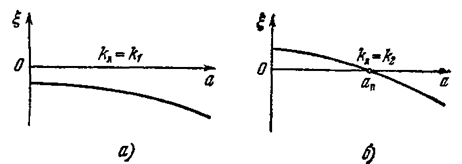
Рис. 6.23.

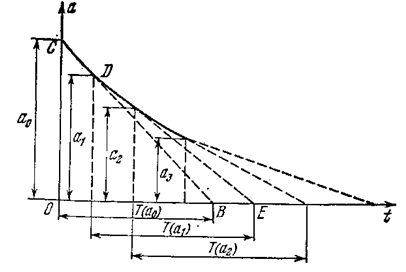
Рис. 6.24.

затухания колебательных переходных процессов при раз­ных значениях параметра kл.

Можно найти огибающую переходного колебательного процесса a (t) во всех этих случаях (рис. 6.24), согласно (6.47), по формуле

Интегрирование (6.52) в конечной форме возможно лишь в простейших случаях. Поэтому приведем графический

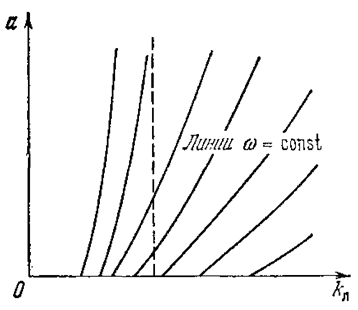
Рис.6.25.

способ построения оги­бающей a (t). Введем в рассмотрение текущую «постоянную времени»

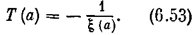
В обыкновенных линейных системах Т = const. Здесь же Т медленно изменяется с изменени­ем амплитуды. Значе­ния Т(а), согласно фор­муле (6.53), берутся из диаграммы качества (рис. 6.22) для каждого значения а при задан­ном kл. Считая Т = const на небольшом промежутке времени, производим графическое построение огибающей a (t) указанным на рис. 6.24 способом. Он настолько прост, что не требует дополнительных к рисунку разъяснений.

Для наглядного представления об изменениях часто­ты переходных колебаний можно, используя уравнения (6.51), на той же плоскости (kл, а) построить линии равных значений частоты w (рис. 6.25).

Приведем пример построения диаграмм качества не­линейных колебательных переходных процессов для си­стемы, показанной па рис. 6.26, где

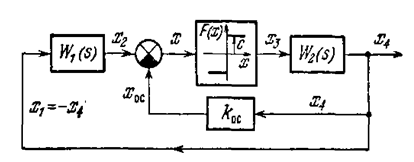
Рис. 6.26.

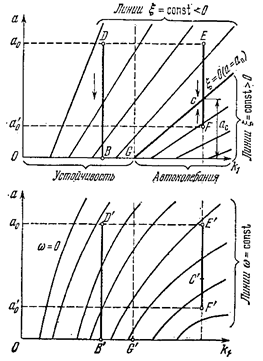
Рис. 6.27.

Гармоническая линеаризация нелинейности дает

Характеристическое уравнение замкнутой системы в результате получает вид

Подставляя в это уравнение l = x + jw, ищем решение в форме (6.47). Выделив вещественную и мнимую части,

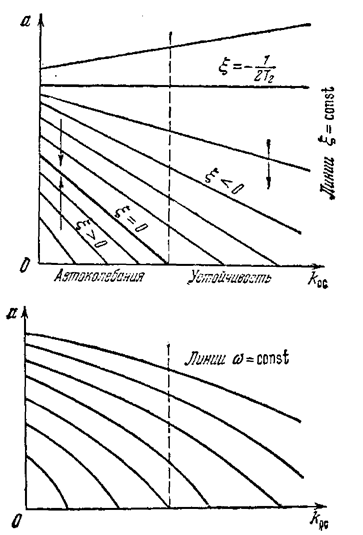
Рис. 6.28.

получим два уравнения (6.51) в виде

Из второго уравнения с учетом значения q(а) находим

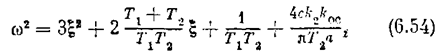
а из первого

где

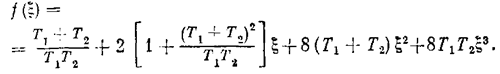
По формулам (6.54) и (6.55) построены диаграммы качества нелинейных колебательных переходных процес­сов в виде линий x = const и w = const по параметру k1

Рас. 6.29.

на рис. 6.27, а по параметру kос - на рис. 6.28. Линии x = 0 на обеих диаграммах соответствуют амплитуде ав­токолебаний. В области автоколебаний, как видно из диаграммы качества, например по линии FC (рис. 6.27), переходные процессы расходятся (x > 0) от состояния равновесия (а = 0) до амплитуды а с и затухаютприбольших начальных амплитудах (x<0), например по отрезку ЕС. В области же устойчивости (см., например, отрезок DB) колебания при любых начальных амплиту­дах затухают (x<0). Изменение частоты колебаний при этом показывают отрезки E'F' и D'B'. Левее линии w = 0 процессы апериодические.

Рис. 6.30.

На рис. 6.29 и 6.30 приведены диаграммы качества, характерные для других видов нелинейностей. Важно отметить, что а случав нелинейной системы такие диа­граммы имели бы вид вертикальных, прямых, таккак x и w там не зависят от амплитуды. Это и видно на рис. 6.30 в зоне линейности, где а < b.

Укажем еще другой способ оценки быстроты затухания переходных процессов в нелинейной системе с од­ной однозначной нелинейностью F(x) (рис. 6.31). Передаточная функция линейной части имеет вид

Нелинейная характеристика F(x) расположена в секторе [0, km] (рис. 6.31, б) и может иметь произвольное очертания. Данный способ оценки быстроты затухания

Рис. 6.31.

переходных процессов основан па применении частотно­го критерия абсолютной устойчивости (лекция 23). На комп­лексной плоскости вместо модифицированной (5.48) стро­ится смещенная частотная характеристика, определяе­мая следующим образом:

где

Основываясь на формулировке критерия абсолютной устойчивости (лекция 23), можно оценить быстроту затухания переходного процесса в системе следующим обра­зом: нелинейная система с устойчивой линейной частью и нелинейной характеристикой, расположенной внутри сектора [0, km], будет обладать показателем затухания, не меньшим данного ½x½, если через точку –1/km можно провести прямую с любым наклоном так, что она не пересечет смещенной характеристики Wсм(w, x). Эта оценка проиллюстрирована на рис. 6.32.

Рис.6.32.

Рис. 6.33.

Можно определить предельное значение km, прикотором в системе имеет место показатель затухания, неменьше ½x½, как показано на рис. 6.33.

Если построить серию смещенных частотных характеристик для разных значений x, то получим зависимость x(km), т. е. зависимость показателя затухания отразмера сектора, в котором лежит нелинейная характеристика.