АВТОКОЛЕБАНИЯ В СИСТЕМАХВЫСОКОГО ПОРЯДКА

План.

1. Случай вещественных корней.

2. Случай равных вещественных корней.

3.Случай комплексных корней.

В качестве исходного материала, используемого в даль­нейшем при изучении нелинейных систем, рассмотрим особые точки линейных систем второго порядка. Уравне­ния линейной системы имеют вид

или в векторно-матричной форме

 

при условии, что матрица А невырожденная, т. е. det А¹ 0 Дифференциальное уравнение фазовых траек­торий, согласно (1.5), имеет вид

Единственной особой точкой (точкой равновесного состоя­ния системы) является точка х 1 = 0, х 2 = 0.

Пусть корни l1 и l2 характеристического уравнения

(здесь.Е—единичная матрица) различны. Путем подста­новки вида х= Ру где Р — некоторая невырожденная матрица, матрицу А можно привести к диагональному виду. Уравнения (1.5) примут вид:

или

Решением этих уравнений является

Рассмотрим фазовые траектории в этой условной си­стеме координат (у1,у2), а затем отобразим фазовые траектории на плоскость исходных координат (х1,х2)

Случай вещественных корней l1,2 Переходный про­цесс — апериодический. Пусть

Исключив t из решения (1.7), получим уравнение фазо­вых траекторий

Если знаки корней l1,2 одинаковы, то с учетом (1.8) имеем l2 /l1 > 1, и фазовые траектории представляются в виде парабол, как показано на рис. 1.15. При этом направление движения изображающей точки М по любой фазовой траектории определяется уравнением (1.7), а именно: случаю l1 < 0, l2< 0 отвечает рис. 1.15,а,

 

Рис. 1.15.

что соответствует затухающим переходным процессам; случай l1 > 0, l2 > 0 (рис. 1.15,б) соответствует рас­ходящимся переходным процессам. Если же знаки корней l1,2 различны, то в урав­нении (1.9) имеем l2/l1<-1, и фазовые траек­тории имеют вид гипер­бол (рис. 1.16).

В случае отрицатель­ных вещественных корней (рис. 1.15, а) особая точ­ка 0 называется точкой типа «устойчивый узел».

В случае положитель­ных вещественных кор­ней (рис. 1.15, б) осо­бая точка 0 называется точкой типа «неустойчи­вый узел».

В случае же вещественных корней разных знаков (рис. 1.16) особая точка 0 называется точкой типа «сед­ло». Седловая точка всегда неустойчива.

 

Рис. 1.16.

Отобразим полученные фазовые портреты линейной системы на плоскость исходных координат (х 1 ,х 2). Ис­пользуем тот факт, что оси парабол и асимптоты гипер­бол (у1,у2) сами являются фазовыми траекториями и при линейном преобразовании останутся прямыми. Их отображение на плоскость (х 1 х 2) примет вид х2 =kx 1. Подставив это соотношение в (1.6), получим

 

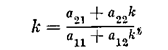
или

 

откуда находим два значения k 1 и k 2. Это дает две пря­молинейные фазовые траектории (рис. 1.17)*)*).

Рис. 1.17.

На рис.1.17 дано расположение также и остальных (криволинейных) фазовых траекторий. Аналогичная картина изображена и на рис. 1.18 для особой точки типа «седло». По какой из фазовых траекторий пойдет переходный про­цесс в системе, определяется начальными условиями х1(t0), х2(t0), которые дают вам координаты начальной точки Мо (рис. 1.17).

Для уточнения такой качественной картины фазовых траекторий можно применить метод изоклин.

Рис. 1.18.

Изоклиной называется линия, соединяющая точки фазовых траекто­рий с одинаковым наклоном касательной, т. е. для каж­дой изоклины dx2/dx1 = с. Поэтому уравнение изоклины, согласно (1.6), имеет вид

Следовательно, любая прямая х2 = kиx1 будет изоклиной с соответствующим значением постоянной с. Задаваясь определенной величиной k и (рис. 1.18), согласно (1.10) находим

 

Нанеся несколько изоклин и зная для каждой из них крутизну наклона с пересекающих ее фазовых траекто­рии, можно уточнить всю картину фазовых траекторий.

Случай равных вещественных корней: l1=l2. В этом случае получается вырожденный узел, устойчивый при l1,2<0 и неустойчивый при l1,2>0 (фазовые траекто­рии показаны в координатах у1, у2 на рис. 1.19, а, б).

 

Рис. 1.19.

Случай комплексных корней l1,2. Переходный про­цесс — колебательный. Пусть

Решения (1.7) принимают комплексный вид

Введя новые переменные с помощью подстановки

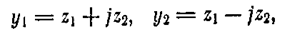
преобразуем решение к вещественной форме

где А и g — произвольные постоянные. Перейдем к полярным координатам (r,j). Тогда

Эти выражения описывают логарифмическую спираль, изображенную на рис. 1.20, а для случая a < 0 и на рис. 1.20, б для a > 0.

Рис. 1.20.

В случае комплексных корней с отрицательной ве­щественной частью (рис. 1.20, а) особая точка 0 называ­ется точкой типа «устойчивый фокус».

В случае комплексных корней с положительной ве­щественной частью (рис. 1.20, б) особая точка 0 называ­ется точкой типа «неустойчивый фокус».

Для преобразования полученных фазовых портретов в исходную систему координат (х1,х2) воспользуемся методом изоклин. Пусть, например, задана система

Корни характеристического уравнения l1,2=-1±j2.

Обозначив х == х 1, х 2 приведем систему к виду

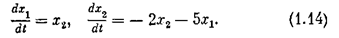
Дифференциальное уравнение фазовых траекторий

Для изоклины х 2 = kи х 1 отсюда находим

Возьмем четыре значения. kи =0, 1, ¥, -1; тогда с = -¥, -7, -2, 3. Соответствующие направления касательных

Рис. 1.21.

к фазовым траекториям показаны на рис. 1.21 стрелками. Ориентируясь по ним, вычерчиваем фазовые траектории. Одна из них изображена на рис. 1.21.

Как частный случай (1.11), при a = 0, т. е. для чисто мнимых корней

l1,2 = ±jb, из (1.12) в полярных координатах на плоскости (z1,z2) получаем

r=A=const. Фазовые траектории имеют вид окружностей (рис. 1.22). При переходе к исходным координатам

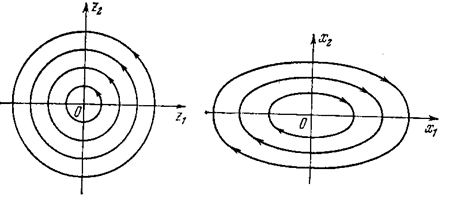
Рис. 1.22. Рис. 1.23.

(х1,х2) получатся эллипсовидные замкнутые кривые (рис. 1.23). Это соответствует периодическим во времени процессам. В случае чисто мнимых корней особая точка 0 (рис. 1.22 и 1.23) называется точкой типа «центр».

ЛЕКЦИЯ 4. Особые точки и фазовые портреты нелинейных систем.

План.

1. Фазовые портреты нелинейных систем.

2. Равновесное состояние.

3. Устойчивый и неустойчивый предельные циклы.

4. Автоколебания системы.

 

Рассмотрим фазовые траектории нелинейной системы второго порядка

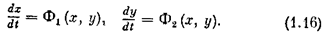
Особые точки, отвечающие равновесным состояниям си­стемы, определяются из условия

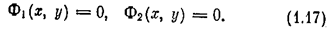
Для выявления типа каждой особой точки уравнения (1.16) линеаризуются при малых отклонениях координат в окрестности особой точки. Затем определяются корни характеристического уравнения линеаризованной системы, по которым, согласно лекции 3, и устанавливается тип осо­бой точки.

Проведем рассмотрение этого вопроса на примере. Пусть заданы уравнения нелинейной системы

Уравнение фазовых траекторий имеет вид

Найдем особые точки согласно условиям (1,17)

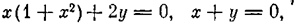
откуда получаем три решения:

1) х= 0, у = 0,

2) x= 1, у = -1,

3) х= -1, у = 1.

Следовательно, система имеет три возможных равновес­ных состояния.

Исследуем характер особых точек.

1. В окрестности точки х = 0, у = 0 линеаризован­ные уравнения имеют вид

Характеристическое уравнение:

Корни l1,2 =±j — чисто мнимые. Следовательно, это особая точка типа «центр».

2. В окрестности точки х = 1, у= -1 вводим малые отклонения в координатах x= х -1, h=у+1. Под­ставляя в уравнения (1.18) х =x+1, у=h-1 и от­брасывая нелинейные члены, получим линеаризованную систему

 

.

Характеристическое уравнение имеет вид

Корни характеристического уравнения

вещественны и имеют разные знаки. Следовательно, это особая точка типа «седло».

3. Рассматривая линеаризованную систему в окрест­ности точки х =- 1, у=1, подстановкой в уравнение (1.18) х =x-1, у=h+1 приходим к тому же урав­нению, что и в предыдущем случае. Следовательно, здесь тоже особая точка типа «седло».

Найдем асимптоты фазовых траекторий в седловых точках. Положив h= kx,, из уравнения фазовых траекторий

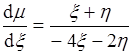
получим

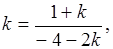
или

откуда находим

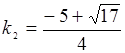
Рис. 1.24.

На рис. 1.24 эти асимптоты показаны в окрестностях соответствующих особых точек. Точка же (0, 0) типа «центр» должна быть окружена замкнутыми кривыми. Исходя из этого, на рис. 1.25 изображен примерный ход фазовых траекторий на всей плоскости.

Для определения направления движения изображаю­щей точки по фазовым траекториям достаточно исследо­вать какую-либо одну точку. Возьмем, например, точку х = 0, у = 1. Согласно уравнениям (1.18) в этой точке имеем dx/dt = -2, dу /dt = 1, т. е. х изменяется в сторо­ну уменьшения, а у- в сторону увеличения. В соответ­ствии с этим и поставлена стрелка па фазовой траекто­рии, проходящей через точку (О, 1), а так как система непрерывна, в ту же сторону будут направлены и все соседние фазовые траектории.

Таким образом выясняется качественная картина фа­зовых траекторий. Отметим, что в данном примере ни одно из трех возможных равновесных состояний системы не является устойчивым.

Рис. 125.

Методом изоклин можно уточнить очертания фазовых траекторий. Уравнение изоклины, согласно (1.19), имеет

вид

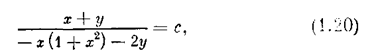
где с—крутизна наклона (dy/dx) пересекающих изокли­ну фазовых траекторий. Например, значению с = 1, т. о. углу наклона траекторий, равному 45°, соответствует, согласно (1.20), изоклина, описываемая уравнением

Она проходит через все три особые точки (штриховая линия на рис. 1.25). В отличие от линейных систем, здесь изоклина криволинейная.

Отметим теперь некоторые общие особенности процес­сов в нелинейных системах.

Рис. 1.26.

Прежде всего, это возможность наличия двух пли нескольких равновесных состоя­ний (особых точек), как уже было видно на приведен­ном примере. В соответствии с этим на фазовой плоскости получаются области с различными типами фазовых тра­екторий. На рис. 1.25, например, эти области разделены жирно обозначенными кривыми. Такие особые кривые, разделяющие области с разными типами фазовых траек­торий, называются сепаратрисами.

Существуют и другого типа особые кривые. Важным типом особых кривых являются предельные циклы — замкнутые кривые, соответствующие периодическим про­цессам, в окрестности которых имеют место колебатель­ные переходные процессы. Если эти фазовые траектории

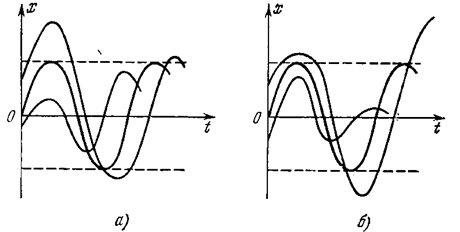
Рис. 1.27.

изнутри и снаружи сходятся к данному предельному циклу (рис. 1.26, а), то мы имеем устойчивый предельный цикл. Если же они удаляются в обе стороны (рис. 1.26, б),— неустойчивый предельный цикл. Возмо­жен и случай двух предельных циклов (рис. 1.26,в), из которых один устойчивый (в данном случае внешний), а второй неустойчивый.

Особая точка О на рис. 1.26 представляет собой в пер­вом случае неустойчивое равновесное состояние, а во втором и третьем — устойчивое. Картина процессов во времени, соответствующая рис. 1.26, а, б, изображена на рис. 1.27, а, б.

Физический смысл устойчивого периодического про­цесса, отвечающего предельному циклу,— автоколебания системы. Это собственные периодические колебания, про­исходящие при отсутствии внешнего периодического воздействия, причем амплитуда и частота автоколебаний не зависит от начальных условий, а определяется внут­ренними свойствами системы. Автоколебания могут воз­никать только в нелинейных системах. Что же касается линейных систем, то в них собственные периодические колебания возможны только на границе устойчивости (l1,2 =±jw), причем амплитуда их определяется на­чальными условиями (см. рис. 1.23).

Физический смысл неустойчивого предельного цикла совсем иной.Как видно из рис. 1.26, б, неустойчивый предельный цикл — это граница областей начальных ус­ловий. При начальных условиях х (to), у(to), лежащих внутри неустойчивого предельного цикла, получается за­тухающий переходный процесс, если же они лежат сна­ружи — расходящийся. Следовательно, равновесное состо­яние О в данном случае устойчиво при небольших на­чальных отклонениях, а при больших — система неус­тойчива. Говорят: система устойчива «в малом» и неус­тойчива «в большом».

Здесь важно отметить, что, в отличие от линейных систем, типы динамических процессов нелинейных си­стем могут существенно зависеть от начальных условий.

Интересно далее отметить, что в первом случае (рис. 1.26, а) единственным устойчивым установившимся состоянием системы является автоколебательный режим. Во втором случае (рис. 1.26, б)—равновесное состояние О. В третьем же случае система имеет два устойчивых установившихся состояния: равновесное О, и автоколеба­ния с большой амплитудой (внешний предельный цикл). Какой из них установится, зависит от начальных условий.

В первом случае говорят, что имеет место «мягкое возбуждение» автоколебаний (т. е. при любых начальных условиях), а в третьем случае—«жесткое возбуждение» автоколебаний, так как, чтобы система вышла на них, не­обходимо начальные условия «забросить» за пределы внутреннего неустойчивого предельного цикла.

Все это будет проиллюстрировано в последующих гла­вах на примерах систем автоматического регулирования. Кроме того, будут проиллюстрированы и многие другие особые свойства нелинейных систем, как, например, от­резки равновесия, скользящие процессы, а также особен­ности, связанные с вынужденными колебаниями и с про­цессами управления, в которых, в отличие от линейных систем, не соблюдается принцип суперпозиции.

 

ЛЕКЦИЯ 5 Переходные процессы и автоколебания релейной системы.

План.

1. Переходные процессы в релейных системах.

2. Линии переключения.

3. Частные случаи релейных характеристик.

 

В данной главе исследование переходных процессов на фазовой плоскости иллюстрируется на примерах об­щего характера, выявляющих основные отличительные особенности процессов в нелинейных автоматических си­стемах.

Рассмотрим систему с релейной характеристикой общего вида. Уравнение динамики объекта (рис. 2.1, а) имеет вид

 

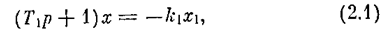
,а уравнение регулятора

где F(x) — релейная характеристика (рис. 2.1,6). Общее

Рис. 2.1.

уравнение динамики системы найдем, если продифферен­цируем уравнение (2.1) и затем подставим в него (2.2). В результате получим выражение

которое можно представить в виде

Отсюда получим дифференциальное уравнение фазовых траекторий

Как видно из заданной характеристики (рис. 2.1,6), нелинейную функцию F(x) можно описать следующим образом:

если у = dx/dt > 0, то

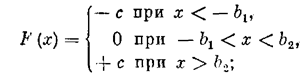
если у == dx/dt < 0, то

В связи с этим на фазовой плоскости (х,у) можно вы­делить три области: (1) F(x)= -с; (2) F(x)=0; (3) F(x) = +с. Эти три области разделены прямыми (на рис. 2.2 они показаны штриховой линией), которые называются линиями переключения.

Такую фазовую плоскость называют многолистной. На каждом листе (1, 2, 3) получится свой вид фазовых траекторий. По линиям переключения эти листы «сшива­ются». Фазовые траектории непрерывно переходят с одного листа на другой (за исключением некоторых особых случаев, где они встречаются).

В области 1(F(x)= -с) уравнение (2.4) принимает вид

 

Проинтегрировав его, получим уравнение фазовых траек­торий в области 1:

Фазовые траектории имеют асимптоту у= k1С, к ко­торой они стремятся при неограниченном увеличении х. Такие фазовые траектории изображены в области 1 на рис. 2.2. Направление их определяется в соответствии с рассмотренным выше правилом (лекция 2, рис. 1.9).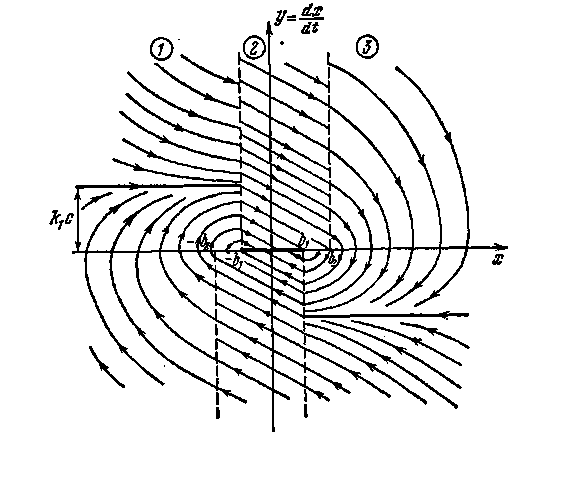

Рис. 2.2.

В области 2 ( F(x)=0) уравнение (2.4) примет вид

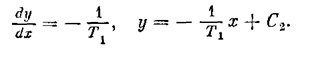
Фазовые траектории - прямолинейные отрезки (см. об­ласть 2 на рис. 2.2).

Наконец, в области 3 (F (х)= +с) уравнение (2.4) примет вид

откуда, аналогично (2.5), уравнение фазовых траекторий будет

Фазовые траектории в области 3 стремятся к асимптоте у= - k1C при уменьшении х (на рис. 2.2).

В целом фазовые траектории принимают спиралевид­ную форму. Это соответствует затухающим колебатель­ным процессам.

 

 

Рис. 2.3.

 

Однако колебательный процесс за­тухает не до нуля, а до некоторого произвольно­го значения (рис. 2.2, 2.3) в интервале –b1 < х < b1, у= 0, т.е. внутри зоны нечувстви­тельности реле (рис.2.1,б). Таким образом, вместо особой точки здесь полу­чается особый отрезок равновесных состояний, показан­ный утолщенной линией на рис. 2.2. По какой из фазо­вых траекторий пойдет переходный процесс в системе, определяется начальными условиями х (to), у (to).

Рис. 2.4.

Рассмотрим теперь частные случаи.

В случае релейной характеристики с зоной нечувст­вительности без петель (рис. 2.4, а) картина фазовых траекторий будет аналогична изображенной на рис. 2.2, с той разницей, что теперь b1= b2= b, т. е. линии пере­ключения будут прямыми без излома на оси х. В случае чисто петлевой гистерезисной релейной ха­рактеристики (рис. 2.4,6) будет отсутствовать область 2 (рис. 2.2). В этом случае имеем

когда

когда

 

Этим определяются линии переключения (штриховые линии на рис. 2.5). Слева от них строим фазовые траек­тории по уравнению (2.5), а справа — по уравне­нию (2.6). Это и показа­но на рис. 2.5. Поскольку ясно видно, что снаружи фазовые траектории обра­зуют сходящиеся спирали, а изнутри расходя­щиеся, то где-то среди них должен быть предельный цикл, к которому они все сходятся. Он выделен утолщенной замкнутой линией (рис. 2.5). Это устойчивый предельный цикл, отвечающий автоко­лебаниям. Амплитуда их определяется точкой пе­ресечения предельного цикла с осью х. Физически такое решение оправдано, ибо в соответствии с нелинейной ха­рактеристикой (рис. 2.4, б) реле не имеет равновесного состояния. Автоколебания происходят около петли реле с амплитудой, несколько превышающей половину ширины петли b.

Рис. 2.5.

Установившийся режим работы такой системы авто­матического регулирования является автоколебательным. Так работают, например, вибрационные регуляторы напряжения сети постоянного тока. Параметры системы должны быть выбраны так, чтобы амплитуда и частота автоколебаний находились в допустимых пределах.

 

ЛЕКЦИЯ 6 Система со скользящим процессом.

План.

1.Уравнения динамики.

2.Фазовый портрет системы.

3.Скользящий процесс.

Проиллюстрируем понятие скользящего процесса на простом примере.

Рис. 2.6.

Пусть задана система автоматического регулирования (рис.2.6), уравнения динамики которой имеют вид

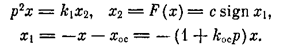
Эти уравнения можно представить в виде

Дифференциальное уравнение фазовых траекторий:

Линия переключения на фазовой плоскости (х, у), следовательно, описывается уравнением

Она показана на рис. 2.7. Справа от этой линии х+ kос > 0. Поэтому уравнение фазовых траекторий (2.8) примет вид

откуда

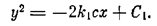
Таким образом, фазовые траектории — это параболы, ветви которых направлены в отрицательную сторону оси х. Положение вершины параболы определяется произ­вольной постоянной С 1, т. е. начальными условиями пере­ходного процесса х (to), у(to).Эти параболы изображены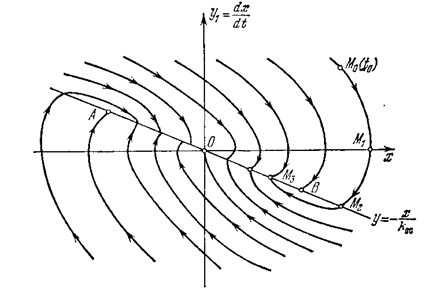

Рис. 2.7.

 

на рис. 2.7 справа от линии переключения. Направление движения изображающей точки М по параболам опреде­ляется прежним правилом (стр. 15, 16, рис. 1.9).

Слева от линии переключения х+ kосу<0, и урав­нение фазовых траекторий (2.8) имеет вид

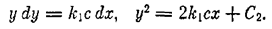
Эти параболы также изображены на рис. 2.7 слева от линии переключения. Видно, что на отрезке линии пере­ключения АВ фазовые траектории встречаются, упираясь в этот отрезок. Это можно расшифровать следующим об­разом. Пусть процесс идет по фазовой траектории 1(рис. 2,8). Как только фазовая траектория пересечет линию переключения ОА, вступит в своп права фазовая траектория 2, которая вернет процесс к отрезку ОА. По тут встретится фазовая траектория 3 и т. д. В результа­те изображающая точка путем вибраций около линии переключения переместится к началу координат О.

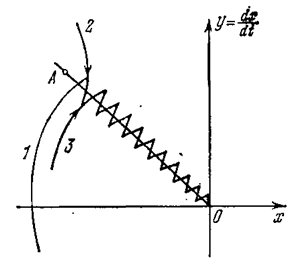
Рис. 2.8.

Такой ход процесса соответствует переключениям релейного эле­мента (рис. 2.6, б) с большой частотой. Тео­ретически частота пере­ключения бесконечна, а амплитуда вибра­ций, изображенных на рис. 2.8, стремится к нулю. Следовательно, теоретически изобра­жающая точка скользит по линии переключения к началу координат — к равновесному состоянию. Процесс такого рода называется скользящим про­цессом.

Найдем закон движения в скользящем процессе. На линии переключения, согласно (2.9), если учесть первое из уравнений (2.7), имеет место уравнение

Решением этого уравнения является

где значения t =0 и х = х 0 считаются в момент попа­дания изображающей точки на линию скользящего про­цесса. Итак, скользящий процесс происходит по экспонен­циальному закону.

Здесь важно отметить следующее. Нелинейная система второго порядка (2.7) на участке скользящего процесса вырождается в линейную систему первого порядка (2.10). При этом закон движения в скользящем процессе не за­висит от параметров прямой цепи системы и определяет­ся только коэффициентом обратной связи. Например, при начальном положении Мо (рис. 2.7) получим фазовую траекторию Мо М1 М2 М3, переходящую в скольжение по линии M 3О. Такой фазовой траектории соответствует про­цесс во времени x(t), изображенный на рис. 2.9, где, как и ранее, отмечены характерные точки.

Рис. 2.9.

Найдем положение концов отрезка скользящего про­цесса А и В на фазовой плоскости (рис. 2.7). Очевидно, что в этих точках касательные к параболам совпадают с линией переключения. Это условие, согласно (2.9), можно записать в виде

тогда из уравнения фазовых траекторий (2.8) получим для точек А и В соответственно условие (2.11) в виде

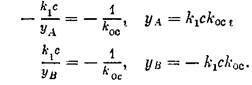
Следовательно, отрезок скользящего процесса АВ тем больше, чем больше коэффициенты усиления прямой цепи и обратной связи.

 

ЛЕКЦИЯ 7 Система с логическим управлением. Учет временного запаздывания.

План.

1. Система угловой стабилизации объекта.

2. Идеальная работа системы управления.

3. Временное запаздывание в системе управления.

Рассмотрим автоматическую систему угловой стабили­зации объекта в среде без сопротивления (стабилизация аппарата в космосе). Структурная схема системы изображена на рис. 2.10. Уравнение динамики объекта, т. е. уравнение вращения объекта вокруг своей оси, имеет вид

где J- момент инерции, w- угловая скорость, М- вра­щающий момент со стороны системы управления. Будем считать, что вследствие некоторых внешних возмущений объект начал вращаться (например, в результате неидеальности процесса отделения от носителя при запуске), и рас­смотрим его стабилизацию с по­мощью системы управления при от­сутствии внешних возмущений.

Рис. 2.10.

Система управления (рис. 2.10.) состоит из двух измерителей: изме­рителя угла j и измерителя уг­ловой скорости w, с которых сигна­лы u1 и u2 снимаются в релейной форме, показанной на рис. 2.11. Эти сигналы поступают в логическое устройство, вырабатывающее нели­нейный закон управления в виде некоторой логической функции Ф(j,w), которая служит управляющим воздействием на включение и выключение газовых сопел, создающих вращательный момент М.

Логическая управляющая функция Ф(j,w) может быть сформирована в различных видах. В простейшем случае можно сформировать ее, как показано на рис. 2.12, использовав для переключении скачки сигналов u1 и u2 (рис. 2.11) при j= ±b1 и w=±b2. При этом Ф=1 соответствует созданию управляющего момента в поло­жительном направлении (против часовой стрелки), Ф= -1 - в отрицательном направлении и Ф=0 - отсут­ствию момента (все сопла выключены).

Указанный выбор логической функции Ф диктуется следующими соображениями. В нулевой зоне -b1<j< b1 (рис. 2.11 и 2.12) сигнала от датчика угла уста­навливаем Ф = 0, так как объект находится вблизи требуемого положения j=0, и регулирующее воздействие не требуется. В I квадранте (рис. 2.12) имеем j > 0 и w= d j/ dt > 0. Следовательно, угол j увеличивается во времени - объект уходит от требуемого положения. Здесь устанавливаем Ф= -1 (направление вращающего мо­мента противоположно направлению угловой скорости w).

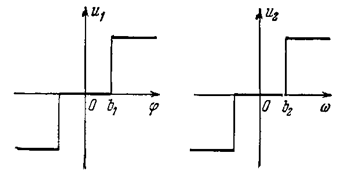
Рис. 2.11.

Аналогично в III квадранте, где знаки j и w отрицатель­ные, включается Ф = +1.

Что касается IV квадранта (рис. 2.12), то там j > 0 и w= d j/ dt < 0, т. е. объект сам возвращается к тре­буемому положению j=0. Здесь можно обой­тись без управляющего момента. Устанавливаем Ф=0. Границей между областью Ф= -1 (в I квадранте) и областью Ф=0 (в IV квадранте) назначаем величину w= -b2 (рис. 2.12), когда сигнал с датчика угловой скорости имеет перескок с нуля к отрицательному значению (рис. 2.11).Ана­логично поступаем и во II квадранте (рис. 2.12).

 

 

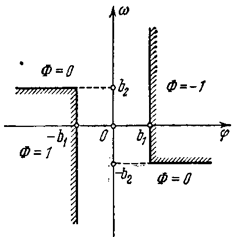
Рис. 2.12.

 

В соответствии с этой схемой строится логическое устройство (рис. 2.10). Его функционирование можно описать таблицей выходного сигнала Ф в зависимости от входных:

 

Сигнал U2 от w	Сигнал U1 от j
-		+
-	+1
	+1		-1
+			-1

 

Здесь приведен пример простейшей логики формиро­вания закона управления. Можно выбирать и другие, более сложные, в зависимости от требований, предъяв­ляемых к системе по экономичности, точности, быстродей­ствию и т.п.

Рассмотрим идеальную работу системы управления (без запаздывания сигналов по всей цепи звеньев). В этом случае уравнение системы управления запишется в виде

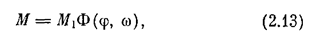
где М1=const - величина управляющего момента, ко­торый создается включаемыми на постоянную тягу га­зовыми соплами; Ф(j,w) - логический закон управления, определяемый в данном случае приведенной выше таб­лицей или согласно графику рис. 2.12.

Общее уравнение системы, согласно (2.12) и (2.13), можно записать в виде

Физический смысл величины с — постоянное угловое ус­корение вращения объекта под действием момента M 1. Дифференциальное уравнение фазовых траекторий:

Фазовую плоскость ограничим по оси абсцисс значения­ми -p £ j £ p (рис. 2.13), причем для вращающегося тела точки (j=±p совпадают.*)*) Этим охватывается полный оборот объекта.

В области, где Ф= -1 (рис. 2.13), уравнения (2.15)

принимают вид

вследствие чего фазовые траектории являются параболами

В области, где Ф= +1, имеем фазовые траектории

Наконец, в области, где Ф == О, получаем прямые линии

Все указанные траектории приведены на рис. 2.13.

Рис. 2.13.

Рассмотрим ход процесса. Пусть начальные условия определяются точкой N0 (рис. 2.13). Процесс пойдет согласно фазовой траектории N0 - 1 - 2. Точка 2 (j=+p) при вращении совпадает с точкой 2 ' (j= -p). Поэтому дальше процесс пойдет в соответствии с фазовой траекторией 2 – 3 – 4 – 5. Как видно из рис. 2.13, точка N1, в которой угол j равен начальному (в точке N0), означает, что объект совершил один полный оборот. За­тем (траектория N1 –3 –4 –5 ) он начал колебательное движение около своей оси. Начиная с точки 5, получаем замкнутую фазовую траекторию 5 –6 –7 –8 –5. Следо­вательно, объект входит в установившийся автоколеба­тельный режим с амплитудой

Своеобразие этого предельного цикла состоит, во-пер­вых, в том, что снаружи фазовые траектории приближа­ются к нему не асимптотически, как было ранее в дру­гих задачах, а за конечное число колебаний (и за ко­нечное время). В описанном выше процессе это было за один оборот плюс один размах колебания. Своеобразие этого предельного цикла заключается также в том, что фазовые траектории внутри него тоже замкнутые и окру­жают отрезок равновесия DE. Поэтому при малых на­чальных отклонениях, лежащих внутри предельного цик­ла, получаются периодические колебания, определяемые начальными условиями. В частности, состояние равнове­сия, возможное только при w0=0 и -b1<j0<b1, не является устойчивым. Особый отрезок DE имеет здесь свойства, аналогичные особой точке типа «центр» (рис. 1.17). Итак, установившимся режимом в данной системе являются автоколебания с амплитудой (2.19).

Введем теперь в рассмотрение временное запаздыва­ние в системе управления. Пусть t1 - величина запазды­вания при включении газовых сопел, а t2 - при их вы­ключении (t2>t1). Поскольку к линии включения со­пел (j=b1) (рис. 2.13) объект подходит с постоянной ско­ростью (горизонтальные фазовые траектории), то за счет запаздывания включения сопел t1 он перейдет за эту линию на величину Dj=wt1. Это значит, что ли­ния включения займет теперь в координатах (j,t1) на­клонное положение (рис. 2.14). Аналогично и в III квад­ранте.

К линии же выключения сопел w= -b2 объект под­ходит с постоянным ускорением — с (параболическая фазовая траектория). Поэтому за счет запаздывания выклю­чения сопел та он перейдет за эту линию на величину Dw= -сt2. Следовательно, линия выключения сопел w= -b2 сместится вниз (рис. 2.14). Аналогично в ле­вой полуплоскости линия выключения w=b2 сместится вверх на величину Dw=ct2.

 

Рис. 2.14.

В соответствии с этим на рис. 2.14 нанесены фазовые траектории. Видно, что предельный цикл за счет запаздываний увеличился в размерах. Амплитуда его

вместо прежней (2.19).

Изменится картина фазовых траекторий и внутри предельного цикла. Там включение сопел будет происхо­дить на линиях FG и F1G1. Выключение же - на линиях FH и F1H1 которые получаются от перехода парабол за линии (j=±b1 на Dw= ct2 соответственно, причем отрезок D (рис. 2.14) определяется по формуле

В результате внутри предельного цикла получаются рас­ходящиеся спиралевидные фазовые траектории. Это соответствует расходящимся колебаниям системы, переходя­щим в предельный цикл. Здесь, как и в предыдущем случае, система попадает в автоколебательный режим изв­не не асимптотически, а за конечное число колебаний.

Рассмотренный подход к учету на фазовой плоскости временного запаздывания в системе эквивалентен в ка­кой-то степени исследованию некоторых свойств системы выше второго порядка. Примерно таким же образом мо­жет влиять на поведение системы учет постоянных времени в системе управления.

Аналогичным способом можно производить учет вре­менного запаздывания и в релейных системах автомати­ческого управления.

 

ЛЕКЦИЯ 8. Системы с переменной структурой.

План.

1. Понятие переменной структуры.

2. Форма скользящего процесса.

 

Переменная структура системы дает дополнительные возможности получения различных желаемых процессов автоматического управления п регулирования. Допустим,

Рис. 2.15.

в системе предусмотрены две разные структуры, разли­чающиеся звеньями 1 и 2 (рис. 2.15). Имеется логическ