ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ

ЛЕКЦИЯ 19 Устойчивость. Функция Ляпунова.

План.

1. Уравнения возмущённого движения.

2. Понятие невозмущённого движения системы.

3. Понятие знакоопределённой функции.

4. Функции Ляпунова.

 

В учебном пособии по линейной теории автоматиче­ского управления и регулирования [23] уже давалось общее понятие устойчивости динамической системы по Ляпунову. Напомним вкратце ход наших рассуждений. Запишем уравнения динамики системы п- го порядка при отсутствии возмущающих воздействий в общем нелинейном виде в нормальной форме Коши:

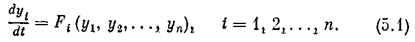
Устойчивость рассматривается как свойство свободного движения системы после начального отклонения ее, вызванного любыми причинами. Пусть (t) обозначает не­который установившийся процесс работы системы, или, как говорят, невозмущенное движение. Отклонение возмущенного движения yi(t), определяемого уравнениями (5.1) при определенных начальных условиях yi(t0), обозначим через х i (t), т. е.

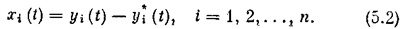
Тогда можно написать уравнения возмущенного движения в отклонениях в виде

при этом невозмущенным движением будет х i= 0. Переменные х i (i = 1, 2, …n) являются координатами состояния системы.

В общем случае конкретный вид уравнений (5.3) зависит от вида установившегося процесса (t), так как эти уравнения получаются из (5.1) подстановкой (5.2).

Поэтому, исследуя эти уравнения необходимо, вообще говоря, оговаривать, об устойчивости какого установившегося режима или невозмущенного движения (t) идет речь.

Геометрически невозмущенное (установившееся) дви­жение (t) системы n-го порядка можно представить

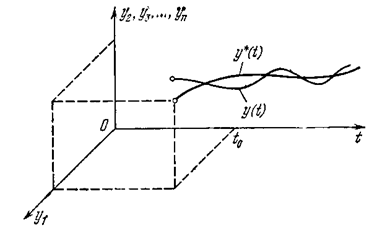
Рис. 5.1.

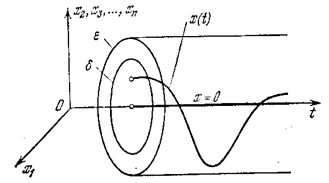
Рис. 5.2.

условно в виде некоторой интегральной кривой в n-мер­ном пространстве с добавленной осью времени t(рис. 5.1). Возмущенное движение yi(t), вызванное на­чальным отклонением при t = to, изобразится другой ин­тегральной кривой (рис. 5.1).

В отклонениях х i(t), т. е. в пространстве координат состояния системы, эта картина возмущенного движения будет выглядеть, как показано на рис. 5.2. При этом не­возмущенное движение 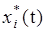= 0 изобразится прямой ли­нией, совпадающей с осью t.

Невозмущенное движение системы 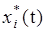= 0 называется устойчивым, если, задав «трубку» сколь угодно малого n-мерного сечения e (рис. 5.2), можно подобрать в на­чальный момент to такую область начальных условий d, зависящую от e, что с увеличением t возмущенное движение х i(t), не выйдет из заданной трубки e.

Аналитическое определение понятия устойчивости по Ляпунову, формулируется следующим образом.

Невозмущённое движение системы 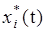=0 называется устойчивым, если при заданном e > 0 сколь бы оно мало ни было, существует такое d > 0, зависящее от e, что при начальных условиях

½ хi (t0)½ < d, i=1, 2,.., п, (5.4)

и дальнейшем движении (t0 < t < ¥) выполняется ус­ловие

½ хi (t)½ < e, i = 1, 2,.., п. (5.5)

Заметим, что в этом аналитическом определении об­ласти e и d, в отличие от рис. 5.2, выглядят «прямоуголь­ными» (в n-мерном пространстве), что не имеет прин­ципиального значения.

Невозмущенное движение 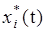= 0 будет неустойчивым, если указанное условие не выполняется хотя бы для од­ного из х i.

Если условия указанного выше определения выполне­ны и имеем х i(t)à0при t à¥, то невозмущенное дви­жение х i = 0 называется асимптотически устойчивым. Если же х i(t)à0 при t ॠпосле любых начальных отклонений, то система называется устойчивой в целом.

Существует еще понятие абсолютной устойчивости, означающее асимптотическую устойчивость системы в целом при любом характере нелинейности внутри опре­деленного класса нелинейностей.

В общем случае в нелинейных системах, в отличие от линейных, устойчивость состояния равновесия не оз­начает, что будут устойчивы и все процессы в системе, так как свойства нелинейной системы меняются с изме­нением величин отклонений координат состояния. Наглядным примером может служить наличие в системе второго порядка неустойчивого предельного цикла (лекция 4). В этом случае при устойчивом состоянии рав­новесия система оказывается неустойчивой при больших начальных отклонениях (выходящих за границу пре­дельного цикла), т. е. система _ устойчива «в малом» и неустойчива «в большом».

При определении понятия устойчивости рассматрива­лись интегральные кривые (рис. 5.1 и 5.2). Если же представить себе не интегральную,

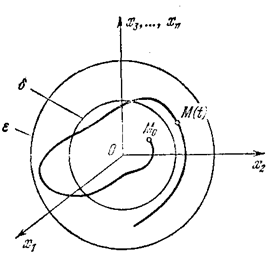
Рис.5.3.

а фазовую траекторию в n-мерном пространстве для системы уравнений (5.3), то в устойчивой системе, согласно определению она будет иметь вид, изображен­ный на рис. 5.3.

В последующих лекциях нам придется иметь дело с непрерыв­ными функциями коор­динат состояния систе­мы V(х 1, х 2, …, х n) обладающими свойст­вом V = 0 при х 1= х 2=…= х n=0. Такая функ­ция V называется знакоопределенной функцией, если во всей рассматриваемой области, содержащей начало ко­ординат, она сохраняет один и тот же знак и обращает­ся в нуль только в начало координат. Например, при n=3

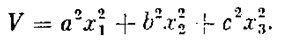
Знакоопределённая функция может быть положитель­но определенной или отрицательно определенной. Если же функция V сохраняет один и тот же знак, но обра­щается в нуль не только в начале координат, то такая Функция называется знакопостоянной (положительной или отрицательной). Например, при п = 3 функция

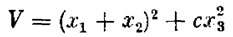
обращается в нуль на прямой х 2=- х 1 и х 3=0-

Наконец, функция V называется знакопеременной, если она в рассматриваемой области не сохраняет одного и того же знака. Например,

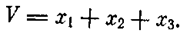
Согласно известному критерию Сильвестра любая квадратичная форма п координат будет знакоопределенной (положительной) тогда и только тогда, когда все главные диагональные миноры матрицы ее коэффициен­тов будут положительными. Например, квадратичная форма

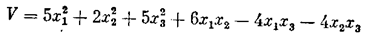
будет положительно определенной, так как для матрицы ее коэффициентов

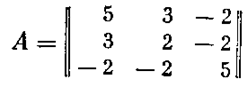
имеем

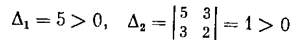
и, наконец,

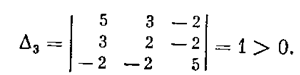
Описанные функции V от координат состояния си­стемы, обращающиеся в нуль в начале координат игра­ют важную роль в теоремах Ляпунова об устойчивости и неустойчивости нелинейных систем и называются функциями Ляпунова.

Пусть имеется нелинейная система, описываемая уравнениями динамики

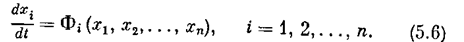
Составим производную функции Ляпунова по времени

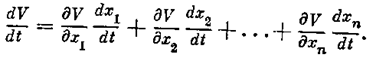
Используя (5.6), в силу уравнений системы, можно записать

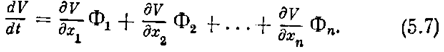
Очевидно,что в результате получается тоже некото­рая функция координат состояния системы

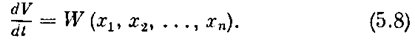
Известно далее, что градиент функции V есть вектор, определяемый проекциями dV/d х i на оси координат, т. е.

Можно ввести вектор Ф(х) с проекциями, отвечающими уравнениям (5.6), а именно:

Вектор Ф(х) будет вектором скорости изображающей точки М в фазовом пространстве (рис. 5.4).

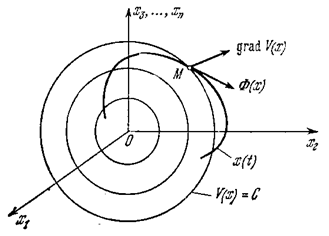
Рис. 5.4.

Согласно (5.7) получаем

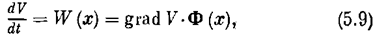
где х— вектор координат состояния системы х = (х 1, х 2,…, х n). Итак, производная функции Ляпу­нова по времени, составленная в силу уравнений систе­мы, представляет собой скалярное произведение гради­ента этой функции на вектор фазовой скорости.

Вектор grad V(x) перпендикулярен к поверхности V == const и направлен в сторону возрастания значений V (рис. 5.4). Если производная dV/dt>0, то, согласно (5.9), вектор фазовой скорости Ф (х) составляет с век­тором grad V (x) острый угол, т. е. фазовая траектории пересекает поверхность V = const в сторону увеличения значений V(x). Если же dV/dt < 0, угол между grad V и Ф (х) тупой, и фазовая траектория идет в сторону уменьшения значений V(х).

 

ЛЕКЦИЯ 20 Теоремы Ляпунова.

План.

1. Теорема Ляпунова об устойчивости.

2. Теорема Ляпунова об асимптотической устойчивости.

3. Теорема Ляпунова о неустойчивости.

4. Методика применения теорем Ляпунова.

Различают теоремы первого и второго методов Ляпунова. Теоремы первого метода Ляпунова использовались при исследовании устойчивости линеаризованных систем [23]. Здесь пойдет речь о теоремах второго, или, как иногда называют прямого метода Ляпунова.

Рис.5.5.

Теорема Ляпунова об устойчивости. Если для системы уравнений (5.6) существует знакоопределенная функция V ( х ), производная которой d V /d t= W( х ) является знако­постоянной противоположного знака, то решение системы х = 0 устойчиво.

На рис. 5.5 представлена геометрическая Иллюстрация этой теоремы, базирующаяся на свойстве (5.9) при условии V (х) > 0 и W (х) £ 0. При W(х) < 0 фазовая траектория пересекает поверхности V = С извне внутрь, а в случае W=0 — может остаться на такой поверхности. Поэтому в теореме говорится просто об устойчивости, но не об асимптотической устойчивости.

Доказательство теоремы. Зададим некоторое значение e > 0 и область значений вектора х = (х 1, х 2,… х n) ограниченную величиной его нормы ÷ê х ÷ê=e. Пусть имеется положительно определенная функция V (х) > 0. Обозначим точную нижнюю грань значений функции V(х) при ÷ê х ÷ê= e через a > 0, т. е.

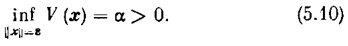
Поскольку V(0)=0, то из непрерывности определенно положительной функции V (х) следует, что можно взять такое значение d > 0. чтобы V (х) < a. при ÷ê х ÷ê<d.

Итак, получаем

Пусть начальные условия лежат внутри области d, т. е.÷ê х (t0)÷ê<d, и следовательно, V (х (t0))<a. Тогда для решения x (t) при t > to функция V (x (t)) будет невозрастающей, так как по условию теоремы

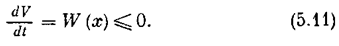
При этом неизбежно

÷ê х (t0)÷ê<e (5.13)

так как, если бы было ÷ê х (t0)÷ê>e, то получилось бы

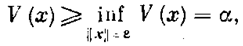
что противоречит (5.12). Теорема доказана.

Из формулировки и из доказательства теоремы вид­но, что теорема Ляпунова дает достаточные условия устойчивости решения х = 0 нелинейной системы. Зна­чит, если условия теоремы удовлетворяются, то система устойчива. Но это не означает, что система но может быть устойчивой и за пределами этих условий. Насколь­ко полно условия теоремы охватят действительную об­ласть устойчивости системы, зависит от выбора функции Ляпунова V.

Теорема Ляпунова об асимптотической устойчивости. Если для системы уравнений (5.6) существует знакоопределенная функция V ( х ), производная которой d V /d t = W( х ) является тоже знакоопределенной, но противоположного знака, то решение системы х = 0 бу­дет устойчивым асимптотически.

Геометрическая иллюстрация теоремы может быть представлена тем же рис. 5.5, но только с той разницей, что при V (х) > 0 имеем здесь W (х) < 0. При этом по свойству (5.9) фазовая траектория, пересекая поверхности V = const извне внутрь, не может остаться на них, а пойдет внутрь вплоть до начала координат, где х = 0 и V (х) = 0.

Ход аналитического доказательства тоже остается прежним, но с изменением (5.11) на

вследствие чего V(x (t)) будет монотонно убывающей функцией с нижним пределом V(0) = 0. Поэтому вместо (5.13) получаем

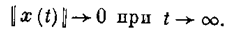
Эта теорема, как и первая, тоже дает достаточные условия устойчивости, а полнота охвата действительной

Рис.5.6.

области устойчивости систе­мы зависит от выбора функ­ции Ляпунова V (х).

Поскольку обе предыду­щие теоремы Ляпунова дают достаточные условия устой­чивости, вообще говоря, не охватывающие всю область устойчивости системы, то мо­жет представить интерес оп­ределение условий, где си­стема становится наверняка неустойчивой.

Теорема Ляпунова о не­устойчивости. Если для си­стемы уравнений (5.6) су­ществует какая-нибудь функция V ( х ), производная которой d V /d t = W( x ) является знакоопределенной функцией, причем в любой сколь угодно малой окрестности начала, координат, имеется об­ласть, в которой знак V ( х ) совпадает со знаком W ( х ), то решение системы х = 0 неустойчиво.

Приведем геометрическую иллюстрацию теоремы для случая п =2 на фазовой плоскости. Пусть функция V (х) знакопеременная с линиями V = const, показан­ными на рис. 5.6, а ее производная d V /d t == W(х) поло­жительно определенная. Видно, что при произвольных начальных условиях фазовая траектория, направляясь в соответствии со свойством (5.9), попадает в область, где V(x)>0 и будет удаляться от начала координат. Если же W(х) является отрицательно определенной, то фазовая траектория удаляется от начала координат в об­ласти, где V(х) < 0.

Аналитически это описывается следующим образом. Пусть производная d V /d t = W(х) знакоопределенная по­ложительная. Зададим некоторое значение e>0. По ус­ловиям теоремы, как бы мала ни была область началь­ных условий d > 0, всегда найдется часть этой области, где V (х) > 0. Тогда функция V(х) с течением времени будет возрастать, т. е. V(x (t)) > V(х (t0)) при t > to.

Рис.5.7.

Поэтому в некоторый мо­мент времени ti значение функции V(х ((t1)) перейдет величину V (÷ê х ÷ê= e) и затем

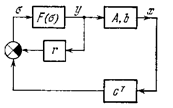
Рис. 5.8.

станет больше этой величины, а вместе с этим бу­дет и ÷ê х ÷ê>e при t > t1 и при любом заданном e > 0, что и говорит о неустойчивости системы.

Перейдем теперь к изложению методики применения теорем Ляпунова для исследования устойчивости нели­нейных систем автоматического управления. Сделаем это для одного (достаточно широкого) класса систем с одной однозначной нелинейностью. Пусть система описывается следующими уравнениями в матричной форме:

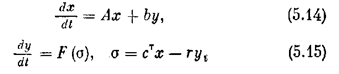
где А — невырожденная матрица n х n коэффициентом, (detA¹0). х — вектор координат х =(х 1, х 2,…, х n), у и d — скалярные координаты, b — матрица-столбец ко­эффициентов b1,b2,…,bn, r —- коэффициент обратной связи, с^т — транспонированная матрица-столбец (с1, с2,…, сn), т. е. матрица-строка, в соответствии с которой

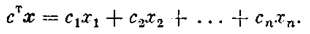
Нелинейная функция F(s) может иметь произволь­ную нечетно-симметричную форму (рис. 5.7), удовлет­воряющую условиям

F(0) = 0, sF(s) > 0 при s¹0. (5.16)

Применительно к реальным системам написанные уравнения можно расшифровать, например, следующим образом: уравнение (5.14) представляет собой уравне­ния динамики управляемого объекта (рис. 5.8). а выражения (5.15) относятся к регулятору — уравнение не­линейного исполнительного устройства (привода) и уравнение измерительно-усилительного устройства и об­ратной связи привода.

Общий порядок системы n+1. В реальных системах измеряются не все координаты х 1, х 2,…, х n состояния объекта. Поэтому некоторые отдельные коэффициенты сi, во втором уравнении (5.15) будут нулями. В реальных системах пулями будет являться и часть элементов матрицы А и столбца b.

Приведём заданную систему (5.14), (5.15) к канони­ческому виду путем замены переменных:

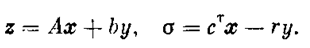
Проделав это, получим систему уравнений

причем будем полагать, что матрица А приведена к диа­гональной форме. Должно соблюдаться условие невы­рожденной общей матрицы системы

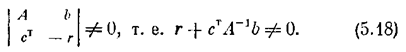
функцию Ляпунова в этом случае рекомендуется [15] брать в виде

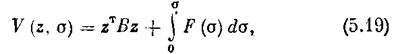
где В — некоторая положительно определенная квадра­тичная форма п координат z. Интеграл в этом выраже­нии тоже является, как легко проверить, положительно определенной функцией (n+1)-й координаты s.

Составим производную функции Ляпунова (5.19) в силу уравнений системы (5.17);

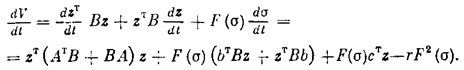
Матрица квадратичной формы В является симметрич­ной, т. е. B^T = В. Поэтому можно сделать следующее преобразование:

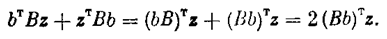
Далее обозначим G = - (A^T B+ВА) и покажем, что матрица G симметричная. В самом деле,

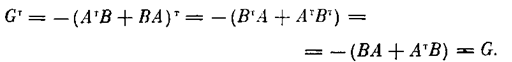
Итак, получаем

Это выражение представляет собой квадратичную форму. Согласно теоремам Ляпунова об устойчивости производная d V /d t должна быть либо знакоопределенной, либо знакопостоянной отрицательной функцией. Обратимся к критерию Сильвестра для установления положительной определенности функции – d V/ d t. По­скольку G является матрицей положительно определен­ной квадратичной фирмы, то первые л неравенств критерия Сильвестра выполняются. Остается потребовать, чтобы

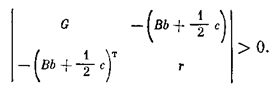
отсюда

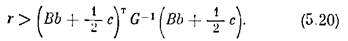
Следовательно, при выполнении условия (5.20) сов­местно с условием (5.18) система будет устойчива асимптотически. Это является достаточным условием асимптотической устойчивости решения z = 0, s = 0.

Видно, что в условия устойчивости (5.20) и (5.18) не вошли никакие параметры нелинейной характеристи­ки F(s). Следовательно, эти условия справедливы при любой форме нелинейности, удовлетворяющей общим требованиям (5.16). Такие условия устойчивости, кото­рые не зависят от конкретной формы нелинейности, на­зываются условиями абсолютной устойчивости системы.
ЛЕКЦИЯ 21 Пример исследования устойчивости методом Ляпунова.

В качестве примера исследуем систему управления курсом самолета (рис. 5.9). Уравнение движения самолета в упрощенном виде имеет вид

где y — угол отклонения оси самолета по курсу, d — угол отклонения руля, F(u) — нелинейная характеристика привода руля (рис. 5.10, д), причем

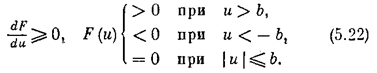
Измерительно-усилительное устройство с обратной связью привода описывается выражением

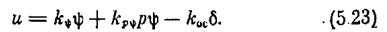
Для перехода к каноническим уравнениям представим уравнение самолета (5.21) в виде

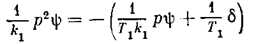
и обозначим

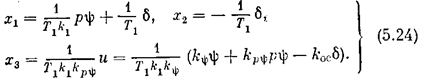
В связи с последним обозначением нелинейная характеристика F(u) заменится на f(х 3) (рис. 5.10, б), где

Рис. 5.9.

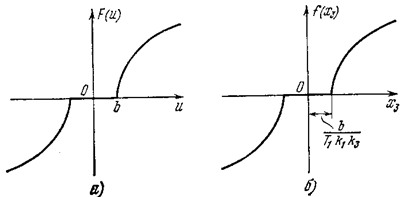
Рис. 5.10.

изменится лишь масштаб по оси абсцисс. Поэтому зона нечувствительности вместо b (рис. 5.10. а) будет иметь размер b/(T1 k1 k py.)

Введем безразмерное время t = t/T1. Тогда система уравнений (5.21), (5.23) преобразуется к каноническому виду

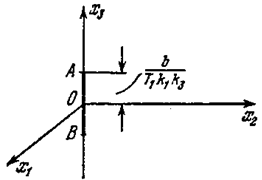
Рис.5.11.

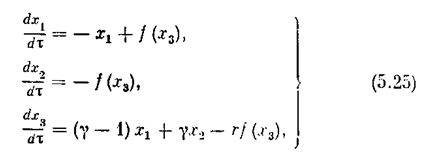
где

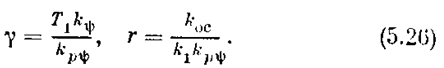
Как видно из уравнений (5.21)— (5.24), установив­шийся режим полета, устойчи­вость которого надо исследо­вать, определяется значениями d = 0, рy=0 ½y½< (b/kpy) или х 1=0, х 2=0, ½ х 3½ < (b/T1 k1 kpy),что иллюстрируется отрезком АВ на рис. 5.11. Рассмотрим отдельно два случая g > 1 и 0<g<1.

1. Случай g > 1 Функция Ляпунова берется в виде

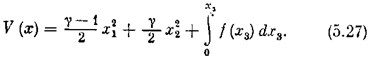
Производная от нее

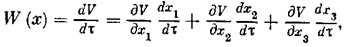
или в силу уравнений системы (5.25) после простых преобразований имеем

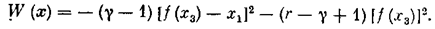
Функция V(х) (5.27) является положительно опре­деленной. Производная же W(х) от нее будет отрица­тельной знакопостоянной при условии

г>g-1, если g>1. (5.28)

Это и является, следовательно, условием устойчивости системы согласно теореме Ляпунова.

Заметим, что d V/ dt = W(х) обращается в нуль, ког­да х 1 = 0 и f (х 3) = 0 при любом значении х 2, т. е. на всей полосе, изображенной па рис. 5.12. Поэтому инте­ресно проверить, не застрянет ли изображающая точна на этой полосе, если фазовая траектория попадет туда. Из уравнений (5.25) на этой полосе имеем

Следовательно, фазовая траектория будет проходить че­рез полосу в направлении, параллельном оси х 3, как показано на рис.5.12. и не застрянет на ней.

 

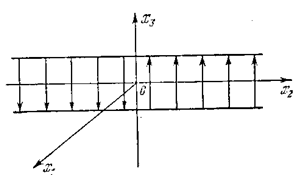
Рис. 5.12.

2. Случай 0<g<l. Функция Ляпунова берется в

виде

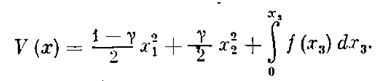
Производная от неё в силу уравнений системы (5,25):

Отсюда условие устойчивости системы, как условие от­рицательного знакопостоянства функции W (х) прини­мает вид

г > 0, если 0 < g < 1. (5.29)

В соответствии с обозначениями (5,26) через исходные параметры системы условия устойчивости (5,28) и (5.29) запишутся в виде соответственно

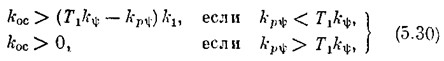
что графически изображено на рис. 5.13, а. Этот резуль­тат физически понятен: коэффициент дополнительной обратной связи kос должен быть достаточно большим, если коэффициент интенсивности введения производной от ошибки kрy взят сравнительно малым. Устойчивость системы не зависит от величины коэффициента обрат­ной связи, если производная введена с достаточно боль­шим коэффициентом.

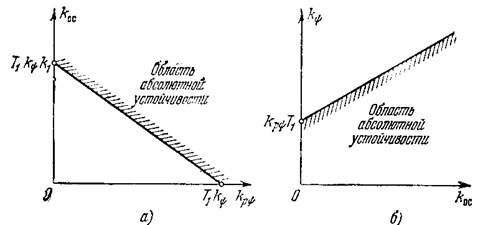
Рис. 5.13.

Согласно (5,30) имеем (при положительных коэффи­циентах)

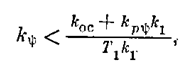
т. е. основной коэффициент усиления автопилота ky мож­но увеличить за счет усиления обоих стабилизирующих средств: kос и kрy, что показано графически на рис. 5.13, б.

Поскольку в условия устойчивости нелинейной систе­мы (5.30) не вошли параметры самой нелинейности, они являются условиями абсолютной устойчивости системы при любой форме однозначной нелинейности, удовлетво­ряющей лишь условию (5.22).

 

ЛЕКЦИЯ 22 Исследование устойчивости методом гармонической линеаризации

План.

1. Пример абсолютной устойчивости.

2. Пример для системы заданной тремя уравнениями.

3. Пример для конкретной формы нелинейности.

 

Для нелинейных систем с одной нелинейностью, обладающих свойством фильтра (лекция 12), можно определять устойчивость как свойство затухания переходных процессов. Это непосредственно вытекает из материала лекции 13, 14 (см., например, рис. 4.16, 4.18). При этом граница устойчивости может быть определена как граница области существования периодических собственных колебаний в системе (К = К гр на рис. 4.16, 4.18), т. е. как граница появления пары чисто мнимых корней в характеристическом уравнении гармонически линеаризованной системы. А это в свою очередь можно определить, приравняв нулю предпоследний определитель Гурвица

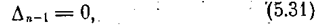
если все остальные определители положительны (для систем третьего и четвертого порядка это означает просто положительность коэффициентов характеристического уравнения).

Ограничимся рассмотрением однозначных нечетных нелинейностей F(x), гармоническая линеаризация которых имеет вид

F(x) = q(a) x. (5.32)

Величина коэффициента q(а) x, как видно из графиков, полученных в лекции 13, 14, меняется в зависимости от а в различных пределах для различных форм однозначных нелинейностей. Для одних — в пределах

0 £ q £ ¥ (5.33)

для других — с некоторыми конечными предельными значениями:

где r1 u г2 — определенные числа для каждой нелинейности (см. лекцию 13, 14). Бесконечный интервал (5.33) охваты­вает все виды однозначных нелинейностей.

Для отыскания границы устойчивости системы (5.31), как границы появления периодических колебаний с какой-либо амплитудой а, надо потребовать выполнения

равенства Dn-1(q) = 0 хотя бы при каком-либо одном значении q в возможном для данной нелинейности ин­тервале (5.33) или (5.34).

Область же устойчивости системы будет лежать с той стороны этой границы, где

при всех возможных для данной нелинейности значени­ях q. Так, в примере 1 лекции 15, 16 имеем k ³ q³ 0 причем граница устойчивости (5.31) получается при q = k,а условие (5.35) выполняется, согласно (4.48), при

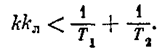
Аналогично в примере 2 лекции 15, 16 имеем 0£ q£ qmax, qmax=2c/pb и граница устойчивости (5.31) достигается при q = qmax, а область устойчивости (5.35)

Если же речь идет об определении абсолютной устойчивости при любой форме однозначной нелинейности, удовлетворяющей лишь условию (5.16), т. е.

F(0) = 0, x F(x) > 0 при х ¹ 0, (5.36)

или (5.22) при наличии зоны нечувствительности, то на­до потребовать удовлетворения условия (5.35) при лю­бом значении q в бесконечном интервале (5.33).

Граница (5.31) области абсолютной устойчивости (5.35) определяется обращением в нуль минимально воз­можногопри 0 £ q£ ¥ значения Dn-1.Это минимальное значение может получаться какпри конечном значении q внутри интервала [0, оо] (рис. 5.14, а),так и при одном изкрайних значений q = 0 или q = ¥ (рис. 5,14, б). Иначе говоря, граница устойчивости мо­жет быть определена из пары условий

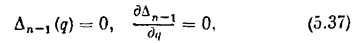
или

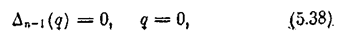
или

Приведем примеры.

Пример 1. В качестве первого примера рассмотрим абсолютную устойчивость той же системы управления курсом самолета(рис. 5.9), которая в лекции 21 исследова­лась методом Ляпунова. Проведя гармоническую линеа­ризацию нелинейности F(u)=q(a) u., получим, согласно

Рис. 5.14.

уравнениям (5.21) — (5.23), характеристическое уравне­ние системы в виде

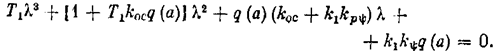
Условия (5.37) принимают вид

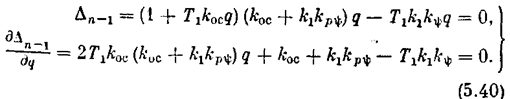
Оба они удовлетворяются при q = 0, если

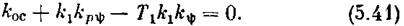
Это— граница устойчивости(типа (5.38)). Условие же устойчивости Dn-1 > 0 при любом положительном значении q, как нетрудно видеть, запишется в виде

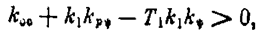
откуда непосредственно вытекают оба условия (5.30) и оба графика рис. 5.13, полученные методом Ляпунова. Такое совпадение имеет место не только в данном при­мере, но и для большого класса нелинейных систем [22].

Рис. 5.15.

Пример 2. Система (рис. 5.15) задана уравнениями

При замене F(x) = q x получаем характеристическое уравнение

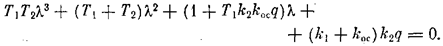
Предпоследний определитель Гурвица

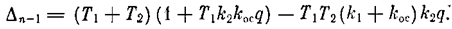
На границе устойчивости, согласно (5.37), имеем

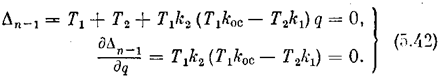
Отсюда - граница абсолютной устойчивости, имеющая место при q=¥;

В предыдущем примере условие устойчивости опреде­лялось условием (5.38), т. е. q = 0. Здесь же имеет место случай (5.39), т. е. q =¥. Очевидно далее, что условие абсолютной устойчивости системы Dn-1 > 0, согласно (5.42), при любом значении q определится неравенством kос >Т2 k1 / T1. В соответствии с этим область устойчиво­сти представлена графически на рис. 5.16.

В [22] имеются примеры, когда условия границы устойчивости (5.37) выполняются не только при край­них значениях q = 0 или q = ¥, как здесь, но при про­межуточных конечных значениях q в соответствии с рис. 5.14. а.

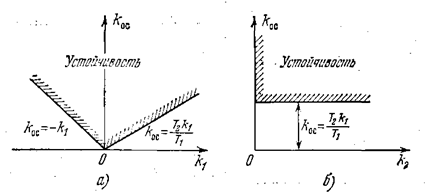
Рис. 5.16.

Рассмотрим теперь влияние конкретной формы нели­нейности на устойчивость нелинейной системы в обоих характерных случаях, приведенных в примерах 1 и 2.

Рис. 5.17.

Пример 3. Пусть в примере 1 задана конкретная форма нелинейности (рис. 5.17, а), для которой коэффи­циент гармонической линеаризации q лежит в интервале

Поскольку граница устойчивости (5.41) определялась наименьшим значением q=0, то она останется той же и при данной конкретной форме нелинейности. Но здесь следующим образом может быть определена область не­устойчивости системы (в целом).

Равенство Dn-1 = 0, определяемое формулой (5.40), при q = 0 дает границу устойчивости, а при всех остальных­

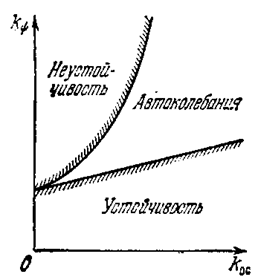
Рис.5.18.

значениях q(a) в интер­вале (5.44) равенство (5.40) определяет автоколебания. Но это возможно, согласно (5.40), только при условии

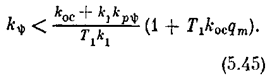
Иначе окажется Dn-1 < 0 при любых значениях q в интерва­ле (5.44), т. е. система не­устойчива.

В результате получаем в данной системетри области (рис. 5.18): устойчивости, автоколебаний и неустойчиво­сти. Здесь граница устойчивости определяется формулой (5.41), а граница неустойчивости, согласно (5.45),

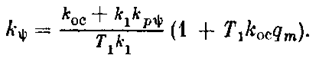
Однако во многих случаях нежелательно входить и в об­ласть автоколебаний. Тогда выбор параметров системы ограничивается областью устойчивости.

Пример 4. Пусть та же конкретная форма нелиней­ности (рис. 5.17, а) фигурирует в примере 2, приведен­ном выше.

Поскольку граница абсолютной устойчивости (5.42) получаетсяпри q=¥, тоограничение значений q ин­тервалом (5.44) расширит область устойчивости.Вместо(5.43) из (5.42) при q=qm получим новую границу

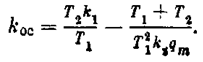
В соответствиис этим область устойчивостипри кон­кретной форме нелинейности вместо общего случая (рис. 5.16) расширится, как показанона рис. 5.19. За этой границей имеет место область автоколебаний.

В заключение заметим, что описанное выше исследо­вание устойчивости нелинейной системы методом гармонической

Рис. 5.19.

линеаризации может быть выполнено и с при­влечением критерия Михайлова вместо критерия Гурвица. Подставив в левую часть характеристического урав­нения гармонически линеаризованной системы l = jw и выделив вещественную и мнимую части

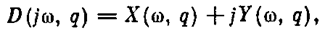
надо потребовать выполнения критерия Михайлова при всех возможных значениях q (5.33) или (5.34).

Иначе границу устойчивости можно определить как границу области, в которой

Х(w, q)=0, Y(w, q)=0,

т. е. как границу области существования автоколебаний. Это бывает удобно в более сложных случаях. Пример будет рассмотрен в конце лекциях 30, 31 (пример 4).

 

ЛЕКЦИЯ 23 Частотный критерий абсолютной устойчивости.

План.

1. Частотный критерий устойчивости В.М.Попова.

2. Теорема Попова.

3. Критерий абсолютной устойчивости.

 

Выше мы уже получали условия абсолютной устойчивости в различных случаях. Аналогично для цели исследования абсолютной устойчивости нелинейных систем служит частотный критерий устойчивости В. М. Попова. Он дает достаточные условия абсолютной устойчивости нелинейной системы но виду частотной характеристики линейной части системы.

Пусть в системе имеется одна однозначная нелинейность F(x) (рис. 5.20). Рассмотрим два случая расположения­

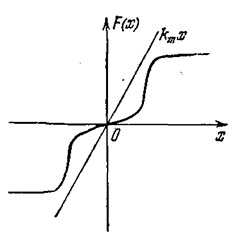
Рис. 5.20.

характеристики: первый — нелинейная характеристика расположена в секторе [0, k m], как на рис. 5.20, второй — в секторе [k0, km], что будет показано ниже.

Начнем с первого случая:

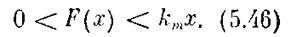
Линейная часть системы описывается уравнением

причем степень многочлена Q(p) больше степени многочлена R(p). Передаточная функция линейной части W(s) =R(s) / Q(s) имеет полюсы с отрицательными вещественными частями, причем допускается наличие не более двух нулевых полюсов.

Приведем без доказательства формулировку теоремы В.М.Попова (доказательство см. в [31]).

Теорема Попова. Состояние равновесия нелинейное системы будет абсолютно устойчивым, если нелинейная характеристика находится в секторе [0, km] и существу­ет такое действительное число h, что при всех w ³ 0 выполняется неравенство

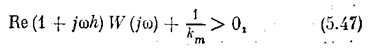
где W (jw) — амплитудно-фазовая частотная характери­стика линейной части системы. Для удобства графического представления этого кри­терия вводится модифицированная частотная характери­стика линейной части

где

Следовательно, график WM(jw) имеет вид, аналогич­ный амплитудно-фазовой характеристике линейной части W(jw) и отличается от нее только масштабом по мнимой

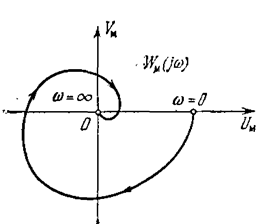
Рис.5.21.

оси (рис. 5.21). Поскольку выражение (5.47) можно записать в виде

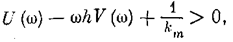
то с подстановкой (5.48) оно преобразуется к виду

 

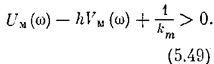
Выражение

представляет собой уравнение прямой на плоскости пря­моугольных координат Uм, Vм. Эта прямая проходит через точку –1/km на оси Uм и имеет крутизну накло­на 1/h.

Отсюда вытекает следующая формулировка.

Критерий абсолютной устойчивости. Состояние равно­весия нелинейной системы абсолютно устойчиво, если не­линейная характеристика F(x) находится внутри сектора [0, km]и можно провести через точку–1/kmпрямую так, что она не пересечет модифицированную частотную характеристику (последняя лежит справа).

На рис. 5.22 показаны случаи, когда критерий абсо­лютной устойчивости выполняется, а па рис. 5.23 — когда не выполняется.