Расчет ошибок позволяет решить одну из главных проблем организации выборочного наблюдения - оценить репрезентативность (представительность) выборочной совокупности.
Различают среднюю и предельную ошибки выборки, которые связаны следующим соотношением: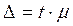 
D - предельная ошибка выборки (доверительная ошибка выборки). Величина предельной ошибки выборки зависит: от колеблемости признака (прямая связь); численности выборки (обратная связь); доверительной вероятности (прямая связь); метода отбора (табл.1). Дает возможность выявить, в каких пределах находится величина генеральной средней:
;
t – коэффициент доверия, определяемый в зависимости от уровня вероятности. Значения t даются в таблицах нормального распределения вероятностей. Например, если t=1, то с вероятностью p=0,683 (или 68,3%) можно утверждать, что разность между выборочной и генеральной средними не превышает одной величины средней ошибки выборки с вероятностью 68,3%;
| Вероятность | Значения t |
| 0,683 | |
| 0,954 | |
| 0,997 |
|
Таблица 1
Формулы для расчета предельной ошибки выборки при различных
способах и методах отбора
| Способ выборки | Повторный отбор | Бесповторный отбор | ||
| для средней | для доли | для средней | для доли | |
| Собственно-случайная |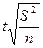 
| 
| 
| 
|
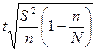
| Механическая | - | Используются формулы собственно-случайной выборки | ||
| Типическая: · пропорциональный отбор; · оптимальный отбор |
|
|
|
|
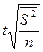
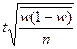
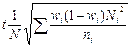
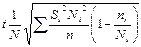
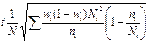
| Серийная | 
| 
| 
| 
|
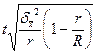
Примечание к таблице 1:
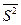- средняя групповая выборочная дисперсия средней: 
;
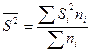где 
- внутригрупповая дисперсия данной (i -й) группы в выборочной совокупности.
- средняя групповая выборочная дисперсия доли: 
.
r – число равных серий в выборочной совокупности;
R - число равных серий в генеральной совокупности;
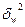- межгрупповая выборочная дисперсия доли: 
;
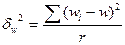где wi – доля единиц, обладающих данным признаком в серии;
w - доля единиц, обладающих данным признаком во всей выборочной совокупности.
Например: в городе проживает 250 тысяч семей. Для определения среднего числа детей в семье была организована 2%-ная случайная бесповторная выборка семей. По ее результатам было получено следующее распределение семей по числу детей:
| Число детей в семье | 0 | 1 | 2 | 3 | 4 | 5 |
| Количество семей | 1000 | 2000 | 1200 | 400 | 200 | 200 |
С вероятностью 0,954 найдите пределы, в которых будет находится среднее число детей в генеральной совокупности.
Решение:
| Число детей в семье xi | Количество семей fi | xi fi | 
|  
| 
|
| 0 | 1000 | 0 | -1,5 | 2,25 | 2250 |
| 1 | 2000 | 2000 | -0,5 | 0,25 | 500 |
| 2 | 1200 | 2400 | 0,5 | 0,25 | 300 |
| 3 | 400 | 1200 | 1,5 | 2,25 | 900 |
| 4 | 200 | 800 | 2,5 | 6,25 | 1250 |
| 5 | 200 | 1000 | 3,5 | 12,25 | 2450 |
| Итого | 5000 | 7400 | - | - | 7650 |
Определим выборочную среднюю: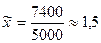 
человека.
Определим выборочную дисперсию: 
человека.
Вычислим предельную ошибку выборки (с учетом p=0,954 t=2)
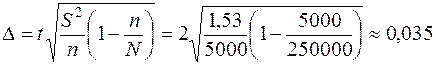
Следовательно, пределы генеральной средней: 
1,5±0,035
Ответ: с вероятностью 95,4% можно утверждать, что среднее число детей в семьях города практически не отличается от 1,5 (т.е. в среднем на каждые две семьи приходятся три ребенка).
|
|
Например: в области, состоящей из 20 районов, проводилось выборочное обследование урожайности на основе отбора серий (районов). Выборочные средние по районам составили: 14,5ц/га; 16; 15,5; 15 и 14 ц/га. С вероятностью 0,683 найдите пределы урожайности во всей области.
Решение:
Рассчитаем общую среднюю:
ц/га
Межгрупповая (межсерийная) дисперсия:
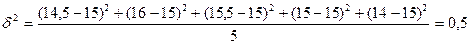
Определим предельную ошибку серийной бесповторной выборки (t=1, p=0,683): 
Следовательно, урожайность в области с вероятностью 0,683 будет находится в пределах 15-0,7£ 
£15+0,7 или 14,3 ц/га£ £15,7 ц/га.