РАБОТЕ № 8
Пример 1. Два стрелка производят по одному выстрелу по одной мишени. Первый попадает в мишень с вероятностью 0,8, второй - с вероятностью 0,6. Найдите вероятность того, что: а) оба стрелка попадут в мишень, б) оба стрелка промахнутся, в) только один стрелок попадет, г) хотя бы один стрелок попадет в мишень.
Решение. Пусть событие А означает, что первый стрелок попал в мишень, событие В - попал второй. По условию Р (А) = 0,8, Р (В) = 0,6.
а) Пусть событие С - оба стрелка попали в мишень, тогда С = АВ. Поэтому, учитывая независимость событий А и В, по теореме умножения вероятностей имеем
Р (С) = Р (АВ) = Р (А) Р (В) = 0,8 × 0,6 = 0,48.
б) Перейдем к противоположным событиям, которые состоят в том, что первый стрелок промахнулся  , второй стрелок промахнулся
, второй стрелок промахнулся  . Тогда событие D =
. Тогда событие D = 
 означает, что оба стрелка промахнулись.
означает, что оба стрелка промахнулись.
Р (D) = Р (
 ) = Р (
) = Р ( ) P (
) P ( )= (1 – Р (А)) (1 – Р (В)) = =0,2 × 0,4 = 0,08.
)= (1 – Р (А)) (1 – Р (В)) = =0,2 × 0,4 = 0,08.
в) Событие Е –только один стрелок попал – можно представить в виде Е = А  + В
+ В  . События А
. События А  и В
и В  несовместные. Поэтому, применяя теорему сложения вероятностей несовместных событий, получим
несовместные. Поэтому, применяя теорему сложения вероятностей несовместных событий, получим
Р (Е) = Р (А  + В
+ В  ) = P (А
) = P (А  )+ Р (В
)+ Р (В  ) =
) =
= P (А) Р ( )+ Р (В) Р (
)+ Р (В) Р ( ) = 0,8 × 0,4 + 0,6 × 0,2 = 0,44.
) = 0,8 × 0,4 + 0,6 × 0,2 = 0,44.
г) Вероятность появления хотя бы одного из совместных событий А, В равна разности между единицей и вероятностью произведения противоположных событий  ,
,  . Пусть событие F – хотя бы один стрелок попал. Тогда
. Пусть событие F – хотя бы один стрелок попал. Тогда
Р (F) = 1 – Р (
 ) = 1 – Р (
) = 1 – Р ( ) P (
) P ( ) = 1 – 0,2 × 0,4 = 0,92.
) = 1 – 0,2 × 0,4 = 0,92.
Пример 2. В первой урне 2 белых и 3 черных шара, во второй – 7 белых и 1 черный. Из первой урны в первую переложили 2 шара, затем наудачу извлекли шар из второй урны. Найдите вероятность того, что выбранный из второй урны шар – белый.
Решение. Если событие А может произойти только совместно с одним из событий Н 1 , Н 2,..., Н  , образующих полную группу несовместных событий (гипотез), то вероятность Р (А) появления события определяется по формуле полной вероятности: Р (А) =
, образующих полную группу несовместных событий (гипотез), то вероятность Р (А) появления события определяется по формуле полной вероятности: Р (А) = 
 Р (H
Р (H  ) Р (А/H
) Р (А/H  ), где Р (H
), где Р (H  ) - вероятность гипотезы H
) - вероятность гипотезы H  , Р (А/H
, Р (А/H  ) - условная вероятность события А при этой гипотезе.
) - условная вероятность события А при этой гипотезе.
Вероятность извлечения белого шара из второй урны после добавления двух шаров из первой урны зависит от состава шаров (по цвету) в этой урне. При этом возможны следующие гипотезы:
Н 1 – из первой урны во вторую переложены два белых шара,
Н 2 – из первой урны во вторую переложен один белый и один черный шар,
Н 3 – из первой урны во вторую переложены два черных шара.
Найдем вероятности этих гипотез. Вероятность каждой гипотезы связана с вероятностью извлечения соответствующих шаров из первой урны. Тогда получим
Р (Н 1 ) =  = 0,1,
= 0,1,
Р (Н 2) =  = 0,6,
= 0,6,
Р (Н 3) =  = 0,3.
= 0,3.
Пусть А – событие, состоящее в извлечении белого шара из второй урны, если предварительно имела место одна из гипотез Нi. Условные вероятности события А будут:
Р (А/H 1) = 9/10, Р (A/Н 2) = 8/10, Р (A/Н 3) = 7/10.
По формуле полной вероятности найдем вероятность извлечения белого шара из второй урны
Р (А) = Р (H 1) Р (А/H 1) + Р (H 2) Р (А/H 2) + Р (H 3) Р (А/H 3) =
= 0,1× 0,9 + 0,6× 0,8 + 0,3× 0,7 = 0,78.
Пример 3. Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго – 0,5, для третьего – 0,8. Мишень не поражена. Найдите вероятность, что выстрелы произведены первым стрелком.
Решение. Если вероятности гипотез до опыта были Р (Н 1), Р (Н 2),..., Р (Н  ), а в результате опыта появилось событие А, то условная вероятность Р (Н
), а в результате опыта появилось событие А, то условная вероятность Р (Н  / A) с учетом появления события А вычисляется по формуле Бейеса:
/ A) с учетом появления события А вычисляется по формуле Бейеса:
Р (Н  / A) =
/ A) =  .
.
Возможны три гипотезы: H 1–на линию огня вызван первый стрелок; H 2 –на линию огня вызван второй стрелок; H 3 –на линию огня вызван третий стрелок. Так как вызов на линию огня любого стрелка равновозможен, то вероятности этих гипотез до опыта равны Р (H 1) = Р (H 2) = Р (H 3) = 1/3.
В результате опыта наблюдалось событие А – после произведенных двух выстрелов мишень не поражена. Условные вероятности этого события равны
Р (А/H 1) = 0,7 × 0,7 = 0,49; Р (А/H 2) = 0,5 × 0,5 = 0,25; Р (А/H 3) = 0,2 × 0,2 = 0,04.
По формуле Бейеса для частного случая, когда вероятности гипотезы опыта равны между собой, находим вероятность гипотезы Н 1 после опыта:
Р (H 1/ A) =  = 0,628
= 0,628
Пример 4. Найдите вероятность того, что в пяти независимых испытаниях событие появится: а) ровно 3 раза, б) не менее трех раз, в) не более трех раз г) хотя бы один раз, – если в каждом испытании вероятность появления этого события равна 0,8.
Решение. Так как число испытаний невелики, то для вычисления искомой вероятности воспользуемся формулой Бернулли:  (k) =
(k) =  , где
, где  – число сочетаний из n элементов по k, q = 1 – p. В рассматриваемом случае:
– число сочетаний из n элементов по k, q = 1 – p. В рассматриваемом случае:
а) вероятность появления события ровно 3 раза в 5 испытаниях равна
P  (3) =
(3) =  =
= 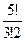
 = 0,2048.
= 0,2048.
б) вероятность появления события не менее трех раз в 5 испытаниях равна
P  (3) + P
(3) + P  (4) + P
(4) + P  (5)= 0,2048 +
(5)= 0,2048 +  + +
+ +  = 0,2048 + 0,4096 + 0,3277 = 0,9421.
= 0,2048 + 0,4096 + 0,3277 = 0,9421.
в) вероятность появления события не более 3 раз в 5 испытаниях равна
P  (0)+ P
(0)+ P  (1) + P
(1) + P  (2) + P
(2) + P  (3)= 1 – P
(3)= 1 – P  (4)– P
(4)– P  (5)=
(5)=
= 1 – 0,4096 – 0,3277 = 0,2629.
г) вероятность появления события хотя бы один раз в 5 испытаниях равна
P  (1) + P
(1) + P  (2) + P
(2) + P  (3) + P
(3) + P  (4) + P
(4) + P  (5) = 1 – P
(5) = 1 – P 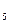 (0) =
(0) =
=1 –  = 1 – 0,0003 = 0,9997.
= 1 – 0,0003 = 0,9997.
При решении б) – г) использована теорема сложения вероятностей несовместных событий, а при решении в), г) – понятие противоположных событий, сумма вероятностей которых равна 1.
Пример 5. Вероятность попадания в цель у стрелка р = =0,8. Производится три выстрела. Построить ряд распределения случайной величины Х – числа попаданий в цель. Найдите математическое ожидание М [ X ] и дисперсию D [ X ].
Решение. Случайная величина Х может принимать значения: 0, 1, 2, 3. Вероятность того, что попаданий не будет р (х= 0) найдем по формуле Бернулли P  (k) =
(k) = 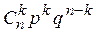 , здесь p = 0,8, q = 1– p= 0,2, n = 3, k = 0.
, здесь p = 0,8, q = 1– p= 0,2, n = 3, k = 0.
p (x= 0) =  =
= 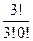
 = 0,008.
= 0,008.
Аналогично найдем p (x= 1) – в результате трех выстрелов будет одно попадание
p (x= 1)=  =
=  0,8 0,4 = 0,096;
0,8 0,4 = 0,096;
p (x= 2)= 0,384; p (x= 3)=0,512.
Ряд распределения будет иметь вид
| x i | |||||
| p i | 0,008 | 0,096 | 0,384 | 0,512 |
Математическое ожидание М [ Х ] и дисперсию D [ Х ] определим по формулам
М [ X ] =  хipi = 0,096 + 2×0,384 + 3×0,512 = 2,4;
хipi = 0,096 + 2×0,384 + 3×0,512 = 2,4;
D [ X ] =  (хi -M [ X ])2 p i ; или
(хi -M [ X ])2 p i ; или
D [ X ] = M [ X 2] – (M [ X ])2.
Предварительно построим ряд распределения случайной величины X 2
| x i 2 | |||||
| p i | 0,008 | 0,096 | 0,384 | 0,512 |
M [ X 2] = 0,096 + 4×0,384 + 9×0,512 =6,24.
D [ X ]=6,24 – (2,4)2 = 0,48.
Пример 6. Дана плотность распределения

случайной величины Х. Найдите параметр а, функцию распределения случайной величины, математическое ожидание М [ X ], дисперсию D [ X ], вероятность выполнения неравенства
0 < X< 1.
Решение. Для определения параметра а воспользуемся основным свойством плотности распределения
 f (x) dx = 1, т.к. при x
f (x) dx = 1, т.к. при x  [-1,1] плотность вероятности равна нулю, то получим равенство
[-1,1] плотность вероятности равна нулю, то получим равенство

 dx = 1,
dx = 1,
Вычислим интеграл

 dx=
dx=
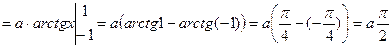
Поэтому  , отсюда
, отсюда  .
.
Функция распределения связана с функцией плотности соотношением
F (x) =  f (x) dx.
f (x) dx.
1) х <- 1, F (x) =  0 dx=0;
0 dx=0;
2) -1  x <1, F (x) =
x <1, F (x) =  0 dx +
0 dx + 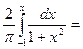

3) х  1, F (x) =
1, F (x) = 
Таким образом, F (x) = 
Математическое ожидание М [ Х ] и дисперсию D [ Х ] определим по формулам
М [ X ] =  х f (x) dx, D [ X ] =
х f (x) dx, D [ X ] =  (х - M [ X ])2 f (x) dx.
(х - M [ X ])2 f (x) dx.
В нашем случае
М [ X ]= 
 d x=
d x= 
 =
= 
D [ X ] = 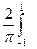
 dх =
dх = 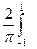 dх –
dх – 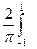
 =
=

Вероятность выполнения неравенства 0 < X < 1 определим по формуле
Р (0 < X < 1) =  f (x) dx = F (1) – F (0) = 1–1/2= 1/2.
f (x) dx = F (1) – F (0) = 1–1/2= 1/2.
Пример 7. Найдите вероятность попадания в данный интервал (15,25) нормально распределенной случайной величины, если известны ее математическое ожидание а = 20 и среднее квадратическое отклонение s = 5.
Решение. Для определения искомой вероятности воспользуемся формулой
Р (a< Х < b) = Ф  - Ф
- Ф  .
.
Здесь Ф (х)= 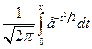 - функция Лапласа, значения которой определяются по таблице. Учитывая, что функция Ф (х) нечетная, получим
- функция Лапласа, значения которой определяются по таблице. Учитывая, что функция Ф (х) нечетная, получим
Р (15< Х <25) = Ф  - Ф
- Ф  =
=
= Ф (1) - Ф (- 1) = 2 Ф (1)= 2× 0,34 = 0,68.
Пример 8. Определите доверительный интервал для оценки с надежностью  =0,95 неизвестного математического ожидания а нормально распределенного признака Х генеральной совокупности, если выборочное среднее равно
=0,95 неизвестного математического ожидания а нормально распределенного признака Х генеральной совокупности, если выборочное среднее равно  = 14, объем выборки n = 25и генеральное среднее квадратическое отклонение
= 14, объем выборки n = 25и генеральное среднее квадратическое отклонение 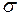 = 5.
= 5.
Решение. Требуется найти доверительный интервал
 –
–  < a <
< a <  +
+  (*)
(*)
Здесь t – значение аргумента функции Лапласа Ф (t). при котором 2 Ф (t)=  . Все величины кроме t известны. Найдем t из соотношения Ф (t)= 0,95/2= 0,475.
. Все величины кроме t известны. Найдем t из соотношения Ф (t)= 0,95/2= 0,475.
По таблице функции Лапласа, зная ее значение, находим значение аргумента t =1,96. Подставив t =1,96,  = 5,
= 5,
n = 25,  = 14 в (*), окончательно получим искомый доверительный интервал
= 14 в (*), окончательно получим искомый доверительный интервал
12,04< a < 15,96.
Приложения
Таблица изображений некоторых элементарных функций
| № п/п | 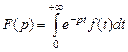
| f (t) |
| 1/ p | ||

| sin at | |
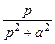
| cos at | |

| 
| |

| sh at | |

| ch at | |

| 
| |

| 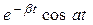
| |

| 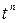
| |

| 
| |

| 
| |

| 
| |

| 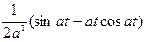
| |

| 
|
Таблица значений функции  ,
, 
| x | ||||||||||
| 0,0 | 0.3989 | |||||||||
| 0,1 | ||||||||||
| 0,2 | ||||||||||
| 0,3 | ||||||||||
| 0,4 | ||||||||||
| 0,5 | ||||||||||
| 0,6 | ||||||||||
| 0,7 | ||||||||||
| 0,8 | ||||||||||
| 0,9 | ||||||||||
| 1,0 | 0.2420 | |||||||||
| 1,1 | ||||||||||
| 1,2 | ||||||||||
| 1,3 | ||||||||||
| 1,4 | ||||||||||
| 1,5 | ||||||||||
| 1,6 | ||||||||||
| 1,7 | ||||||||||
| 1,8 | ||||||||||
| 1,9 | ||||||||||
| 2,0 | 0.0540 | |||||||||
| 2,1 | ||||||||||
| 2,2 | ||||||||||
| 2,3 | ||||||||||
| 2,4 | ||||||||||
| 2,5 | ||||||||||
| 2,6 | ||||||||||
| 2,7 | ||||||||||
| 2,8 | ||||||||||
| 2,9 | ||||||||||
| 3,0 | 0.0044 | |||||||||
| 3,1 | ||||||||||
| 3,2 | ||||||||||
| 3,3 | ||||||||||
| 3,4 | ||||||||||
| 3,5 | ||||||||||
| 3,6 | ||||||||||
| 3,7 | ||||||||||
| 3,8 |
Таблица значений функции  ,
, 

| x | ||||||||||
| 0,0 | 0,00000 | |||||||||
| 0,1 | ||||||||||
| 0,2 | ||||||||||
| 0,3 | ||||||||||
| 0,4 | ||||||||||
| 0,5 | ||||||||||
| 0,6 | ||||||||||
| 0,7 | ||||||||||
| 0,8 | ||||||||||
| 0,9 | ||||||||||
| 1,0 | ||||||||||
| 1,1 | ||||||||||
| 1,2 | ||||||||||
| 1,3 | ||||||||||
| 1,4 | ||||||||||
| 1,5 | ||||||||||
| 1,6 | ||||||||||
| 1,7 | ||||||||||
| 1,8 | ||||||||||
| 1,9 | ||||||||||
| 2,0 | ||||||||||
| 2,1 | ||||||||||
| 2,2 | ||||||||||
| 2,3 | ||||||||||
| 2,4 | ||||||||||
| 2,5 | ||||||||||
| 2,6 | ||||||||||
| 2,7 | ||||||||||
| 2,8 | ||||||||||
| 2,9 | ||||||||||
| 3,0 | 0,49865 | 3,1 | 3,2 | 3,3 | 3,4 | |||||
| 3,5 | 3,6 | 3,7 | 3,8 | 3,9 | ||||||
| 4,0 | ||||||||||
| 4,5 | ||||||||||
| 5,0 |