4.1. Структурная группа 2-го класса 1-го вида
Известны: внешние силы Р и2 и Р и3, а также точки их приложения К2 и К3.
Найти: реакции в кинематических парах А, В и С.
Рис. 4.1. План структурной группы 2 класса 1 вида
Последовательность решения:
1. Строим структурную группу в масштабе длин mL.
2. Наносим на неё все внешние силы (Р и2 и Р и3).
3. В кинематических парах А и С действие «отброшенных» звеньев 1 и 0 заменяем силами реакций R 1-2 и R 0-3, разложив каждую из них на нормальную и тангенциальную составляющие: 
, 
и 
, 
.
4. Составляем уравнение равновесия структурной группы:
; или 
(1)
5. Вычисляем величины тангециальных сил; для этого используем условие, что моменты всех сил, приложенных к звену 2 или звену 3, относительно точки В, равны нулю:
; 
, откуда 
;
; 
, откуда 
.
Следует учитывать, что если в процессе решения этих уравнений тангенциальные силы получены с отрицательным знаком, то на плане структурной группы предварительно выбранные их направления следует поменять на противоположные.
6. Неизвестные 
и 
находим путём графического изображения векторного уравнения (1) в масштабе, то есть, строим план сил структурной группы (рис.4.2).
Для построения плана сил выбираем масштаб: 
, [Н/м],где 
– длина вектора, изображающего силу 
на плане сил, выбирается произвольно; при выборе учитываются два условия: чтобы план сил разместился на отведённом месте чертежа, а масштаб был удобен для расчётов (был «круглым» числом).
Переводим (пересчитываем) силы уравнения (1) в векторные отрезки с длинами: 
, [мм]; 
, [мм]; 
, [мм].
Тогда уравнение (1) запишется в виде:
(2).
Построение плана сил ведём в последовательности написания уравнения (2):
Рис. 4.2. План сил структурной группы.
7. Вычисляем реакции: 
8. Определяем реакцию в кинематической паре В. Для этого составляем векторное уравнение равновесия звена 2 или звена 3; например, условие равновесия звена 2 можно записать в виде:
(3).
Так как и 
известны, то построив план сил звена 2 (то есть графически изобразив уравнение (3)), получим 
: 
Рис. 5.1. План сил звена 2.
5.2. Структурная группа 2-го класса 2-го вида.
Условие равновесия структурной группы:
.
Величина тангенциальной составляющей
вычисляется по формуле:
;
Рис. 5.3. План структурной группы 2 класса второго вида.
, 
– берут из построенного плана сил, а 
–из уравнения равновесия
ползуна 
.
5.3. 
Структурная группа 2-го класса 3-его вида
5.4.
Рассмотрим равновесие звена 3: 
задана; 
; 
отсюда 
; Величину и направление R находим из плана сил:
Рис. 15. План сил структурной группы 
.
5.5. Силовой анализ ведущего звена
Вариант 1. Ведущее звено – зубчатое колесо или кривошип, 
.
Здесь берём из силового анализа присоединённого к звену структурной группы. 
|| OA (из теоремы о трёх силах, действующих на тело, которые обязательно пересекаются).
Условие равновесия звена (1): 
.
Строим план сил звена (1) в масштабе 
, записав уравнение 
;
Уравновешивающая сила 
;
Реакция в кинематической паре О 
.
Вариант 2. Ведущее звено – муфта скольжения.
Условие равновесия звена 1: 
,
откуда 
.
Уравнение моментов относительно О:
,
откуда 
.
5.6. Теорема о «жёстком» рычаге Н.Е.Жуковского
Теорема используется для определения уравновешивающей силы или уравновешивающего момента 
и 
без предварительного определения реакций в кинематических парах механизма.
Она является графической интерпретацией принципа возможных перемещений. Для реального механизма возможные перемещения являются реальными.
Вывод теоремы:
Сумма работ всех внешних сил, приложенных к звеньям механизма, равна нулю:
, (1)
где 
– все внешние силы, в то числе инерции и все, действующие на звенья
механизма (силы реакции не в счёт);
– элементарные перемещения точек приложения этих сил;
– угол приложения внешних сил, или угол давления.
Разделим уравнение (1) на 
и получим:
, (2)
То есть сумма мгновенных мощностей (
) равна нулю. Для определения величины мгновенных мощностей можно выполнить и такое решение:
Дано звено ВС с 
и 
. Построим план скоростей, повёрнутый на 900; здесь 
; 
. Вычислим момент силы
относительно полюса Рv:
. (3)
С учётом этого уравнения уравнение (2) можно
записать так:
. (4)
|
, то
– запись теоремы Жуковского. (5)
Алгебраическая сумма мощностей всех внешних сил, приложенных в соответствующие точки повёрнутого на 900 плана скоростей, относительно полюса равна нулю.
Последовательность определения по теореме Н.Е.Жуковского:
1. Построить повёрнутый на 900 (в любую сторону) план скоростей механизма.
2. В соответствующие точки плана скоростей приложить все ранее определённые внешние силы (включая силы инерции и силы веса), действующие на механизм, в том числе и уравновешивающую силу .
3. Составить уравнение вида (5). Плечи моментов сил брать из повёрнутого плана скоростей.
4. Из составленного уравнения определить .
Пример:
,
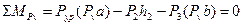отсюда 
.
Если получим с отрицательным знаком, то её предварительно выбранное
направление следует поменять на противоположное.