На разных этапах проектирования встает задача выбора наилучшего варианта из множества допустимых проектных решений, удовлетворяющих предъявленным требованиям.
Процесс принятия решения при оптимальном проектировании характеризуют следующие основные черты: наличие цели (критериев оптимальности) и альтернативных вариантов проектируемого объекта, и учет существенных факторов при проектировании.
Понятие «оптимальное решение» при проектировании имеет вполне определенное толкование — лучшее в том или ином смысле проектное решение, допускаемое обстоятельствами. В подавляющем большинстве случаев одна и та же техническая задача может быть решена несколькими способами, приводящими не только к различным выходным характеристикам, схемам и конструкциям, но даже и к физическим принципам, положенным в основу построения объекта. При этом одно из решений может превосходить другое по одним свойствам и уступать ему по другим. В этих условиях часто чрезвычайно трудно сказать, не только какая из систем оптимальна, но даже какая из них предпочтительнее.
Если выделяют один параметр, который характеризует свойства, то этот параметр принимается за целевую функцию. При этом другие параметры подпадают под категорию ограничений. При решении однокритериальных задач применяется математический аппарат исследования операций. При создании вычислительной сети в большинстве случаев однокритериальные задачи не удовлетворяют полученному решению. Сложные ВС характеризуются многими параметрами (емкость памяти, время счета, пропускная способность каналов и т. п.), определяющими ее качество. Среди этих параметров есть такие, значения которых желательно всемерно увеличивать, но есть и такие, которые желательно минимизировать.
|
|
Таким образом, ограничения и связи между отдельными параметрами ВС приводят к необходимости идти на компромисс и выбирать для каждой характеристики не максимально возможное в принципе значение, а меньшее, но такое, при котором и другие важные характеристики тоже будут иметь приемлемые значения. Поэтому необходимо принимать во внимание всю совокупность характеристик ВС. Задачи проектирования, проводимые по нескольким критериям оптимизации, носят название многокритериальных, или задач векторной оптимизации.
Известные методы векторной оптимизации прямо или косвенно сводят решаемые задачи к задачам скалярной оптимизации, т. е. частные критерии 
тем или иным способом объединяются в составной критерий, 
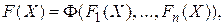который затем максимизируется (или минимизируется). Если составной критерий отражает физическую суть ВС и вскрывает объективную связь между частными критериями и составным критерием, то оптимальное решение является объективным.
На практике из-за сложности обычно составной критерий объединяет частные, что ведет к субъективности решения; такой критерий является обобщенным, или интегральным. В зависимости от того, каким образом частные критерии объединяются в обобщенный критерий, различают критерии аддитивные, мультипликативные и минимаксные (максиминные).
Если оптимизация ведется без учета статистического разброса характеристик, то соответствующий критерий оптимальности называют детерминированным критерием; если разброс параметров учитывается, то имеем критерий статистический. Статистический критерий оптимальности наиболее полно отражает качество ВС, но его использование требует больших затрат машинного времени.
|
|
Рассмотрим способы выбора критериев оптимальности.
Частные критерии
При проектировании по частным критериям в качестве целевой функции F(X) принимается наиболее важный выходной параметр проектируемой ВС, все остальные параметры в виде соответствующих условий работоспособности относятся к ограничениям. В этом случае задача оптимального проектирования является однокритериальной задачей математического программирования: максимизировать (или минимизировать) значение целевой функции 
при наличии ограничений на параметры ВС.
Из постановки задачи вытекает, что параметры, для которых выполняются ограничения в виде строгих неравенств, имеют определенный запас по сравнению с заданными техническими требованиями. Ряд параметров, для которых условия работоспособности имеют вид неравенств, запасов вообще не имеет, и любые изменения технических требований для этих параметров приводят как к изменению характеристик и структуры проектируемого объекта, так и к изменению значения целевой функции.
Частные критерии используются при проектировании ВС различного назначения.
Аддитивные критерии
В этих критериях целевая функция образуется путем сложения нормированных значений частных критериев. Частные критерии имеют различную физическую природу и в соответствии с этим — различную размерность. Поэтому при образовании обобщенного критерия следует оперировать не с «натуральными» критериями, а с их нормированными значениями. Нормированные критерии представляют собой отношение «натурального» частного критерия к некоторой нормирующей величине, измеренной в тех же единицах, что и сам критерий. При этом выбор нормирующего делителя должен быть логически обоснован. Возможны несколько подходов к выбору нормирующего делителя.
|
|
Первый подход предлагает принимать в качестве нормирующего делителя директивные значения параметров, заданные заказчиком. Логически слабым моментом такого подхода является негласное предположение того, что в ТЗ на проектируемую ВС заданы оптимальные значения параметров объекта, и что совокупность заданных значений критериев рассматривается как образцовая.
Второй подход предполагает выбор в качестве нормирующих делителей максимальных значений критериев, достигаемых в области существования проектных решений (в области компромисса). Возможен подход, при котором в качестве нормирующих делителей выбирают разность между максимальным и минимальным значениями критерия в области компромисса.
Выбор подхода к формированию безразмерной формы частных критериев носит иногда субъективный характер и должен обосновываться в каждом конкретном случае. Пусть при проектировании ВС существует п частных критериев. Тогда целевая функция задачи оптимизации в случае применения аддитивного критерия определяется
где 
— весовой коэффициент 
частного критерия;
— 
нормирующий делитель;
— нормированное значение частного критерия.
Такая целевая функция позволяет осуществить компромисс, при котором улучшение значения одного нормированного частного критерия компенсирует ухудшение значений других.
Введение весовых коэффициентов должно учитывать различную значимость частных критериев при формировании аддитивного критерия. Определение весовых коэффициентов сталкивается с серьезными трудностями и обычно сводится либо к использованию формальных процедур, либо к применению экспертных оценок. С появлением обобщенного критерия исчезают логические проблемы, связанные с установлением взаимосвязей между частными критериями различной размерности и выбором наилучшего варианта ВС, и остаются лишь вычислительные трудности. Но аддитивный критерий имеет ряд недостатков, главный из которых состоит в том, что он не вытекает из объективной роли частных критериев в функционировании ВС и выступает поэтому как формальный математический прием, придающий задаче удобный для решения вид.
Другой недостаток заключается в том, что в аддитивном критерии может происходить взаимная компенсация частных критериев. Это значит, что значительное уменьшение одного из критериев вплоть до нулевого значения может быть покрыто возрастанием другого критерия. Для ослабления этого недостатка следует вводить ограничения на минимальные значения частных критериев и их весовых коэффициентов.
Несмотря на слабые стороны, обобщенный аддитивный критерий позволяет в ряде случаев успешно решать многокритериальные задачи и получать полезные результаты.