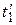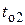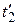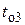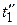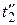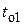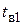Расчетные методы определения вероятностных показателей надежности в зависимости от используемых математических средств можно подразделить на аналитические и имитационные.
Предварительно проанализируем вопрос о необходимой и достаточной номенклатуре определяемых показателей надежности систем, поскольку полный перечень их даже для абстрактного объекта достаточно велик и часть их может быть получена из других (см. гл. 3). Если рассматривается восстанавливаемый объект с L возможными состояниями, то как минимум требуется обычно определить L показателей – частоты попадания объекта в эти состояния или средние времена нахождения объекта в них. Если же необходимо знать еще и частоты того, из каких состояний объект переходит в данное, то минимальное число показателей возрастает до L (L- 1). Слово "минимальное" здесь имеет тот смысл, что нас не интересуют законы распределения времен нахождения объекта в тех или иных состояниях, а мы довольствуемся лишь средними временами нахождения объекта в этих состояниях или полагаем, что эти времена подчиняются экспоненциальным законам.
Для восстанавливаемого объекта, имеющего всего два состояния, минимальное количество показателей также равно двум. Это могут быть средние времена нахождения его в этих состояниях либо один из них в сочетании с комплексным показателем, например коэффициентом готовности (или неготовности), характеризующим одновременно и другое единичное свойство.
В случае невосстанавливаемого объекта минимальное число показателей сокращается и для объекта с двумя состояниями требуется всего один показатель.
4.3.3.1. Аналитические методы. Общий случай. Эти методы построены на использовании теорем теории вероятностей (сложения, умножения вероятностей, формулы полной вероятности и др.). С их помощью устанавливаются связи между вероятностями событий и состояний элементов с событиями и состояниями системы. В самом общем виде показатель безотказности – вероятность того, что система, находясь в состоянии 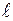 , не снизит свой уровень работоспособности ниже
, не снизит свой уровень работоспособности ниже 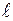 -го уровня за заданное время t – можно записать так:
-го уровня за заданное время t – можно записать так:
|
|
P 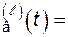 P
P 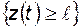 при
при 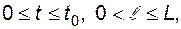 (4.25)
(4.25)
а показатель восстанавливаемости – вероятность того, что система, находясь в состоянии 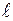 , за заданное время t повысит уровень своей работоспособности выше
, за заданное время t повысит уровень своей работоспособности выше 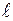 -го уровня:
-го уровня:
P 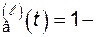 P
P 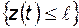 при
при 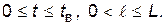 (4.26)
(4.26)
Комплексный показатель – коэффициент готовности как вероятность застать систему в работоспособном состоянии 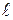 -го уровня – определится как
-го уровня – определится как
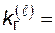 P
P 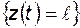 . (4.27)
. (4.27)
В зависимости от способа представления функции 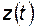 системы и принимаемых допущений разработан ряд аналитических методов расчета показателей надежности для абстрактной системы.
системы и принимаемых допущений разработан ряд аналитических методов расчета показателей надежности для абстрактной системы.
4.3.3.2. Аналитический метод на основе марковского процесса. Процесс, протекающий в системе, называют марковским (или потоком без последействия), если для каждого момента времени вероятность любого состояния системы в будущем зависит только от состояния системы в настоящий момент и не зависит от того, каким образом система пришла в это состояние. Для того чтобы такой процесс протекал в системе, необходимы простейшие (пуассоновские, стационарные) потоки отказов и восстановлений элементов системы, т.е. с 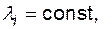
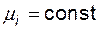 (законы распределения времени работы до отказа и времени восстановления элементов – экспоненциальные).
(законы распределения времени работы до отказа и времени восстановления элементов – экспоненциальные).
|
|
Экспоненциальность законов является первым допущением в этом методе, вторым – элементы могут находиться только в двух состояниях (работоспособном и неработоспособном). Искомые вероятностные показатели здесь определяются с использованием структурно-функционального представления системы в виде графа состояний и переходов (см. рис. 4.2 и 4.3).
Пусть процесс отказов и восстановлений элемента обладает свойствами марковского случайного процесса, а элемент может находиться в двух состояниях: 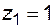 - безотказной работы,
- безотказной работы, 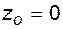 - состоянии отказа (см. рис. 4.2). Определим соответствующие вероятности состояний элемента
- состоянии отказа (см. рис. 4.2). Определим соответствующие вероятности состояний элемента 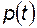 и
и 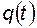 в произвольный момент времени t при различных начальных условиях.
в произвольный момент времени t при различных начальных условиях.
Для любого момента времени сумма вероятностей 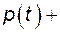 +
+ 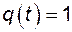 - вероятность достоверного события. Зафиксируем момент времени t и найдем вероятность p
- вероятность достоверного события. Зафиксируем момент времени t и найдем вероятность p 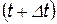 того, что в момент
того, что в момент 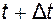 элемент находится в работоспособном состоянии. Это событие осуществляется при двух условиях.
элемент находится в работоспособном состоянии. Это событие осуществляется при двух условиях.
1. В момент t элемент находился в состоянии 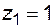 и за время
и за время 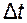 не произошло отказа. Вероятность работоспособного состояния элемента определяется по правилу умножения вероятностей независимых событий. Вероятность того, что в момент t элемент был в состоянии
не произошло отказа. Вероятность работоспособного состояния элемента определяется по правилу умножения вероятностей независимых событий. Вероятность того, что в момент t элемент был в состоянии 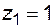 , равна
, равна 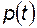 , а того, что за время
, а того, что за время 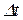 он не отказал -
он не отказал - 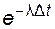 . С точностью до величины высшего порядка малости можно записать
. С точностью до величины высшего порядка малости можно записать
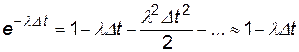 . (4.28)
. (4.28)
Поэтому вероятность данной гипотезы равна 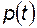
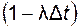 .
.
2. В момент времени t элемент находится в состоянии 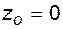 (в состоянии отказа), за время
(в состоянии отказа), за время 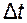 восстановление закончилось и элемент перешел в состояние
восстановление закончилось и элемент перешел в состояние 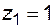 . Эту вероятность также определим по правилу умножения вероятностей независимых событий. Вероятность того, что в момент времени t элемент находился в состоянии
. Эту вероятность также определим по правилу умножения вероятностей независимых событий. Вероятность того, что в момент времени t элемент находился в состоянии 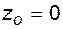 , равна
, равна 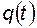 , а вероятность того, что восстановление закончилось за время не более
, а вероятность того, что восстановление закончилось за время не более 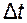 , определим из (3.22) как
, определим из (3.22) как 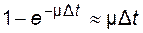 при тех же допущениях, что и для (4.28). Следовательно, вероятность второй гипотезы равна
при тех же допущениях, что и для (4.28). Следовательно, вероятность второй гипотезы равна 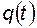
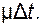
|
|
Вероятность работоспособного состояния элемента в момент 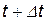 определяется вероятностью суммы независимых несовместимых событий при выполнении обеих гипотез:
определяется вероятностью суммы независимых несовместимых событий при выполнении обеих гипотез:
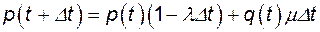 (4.29)
(4.29)
или
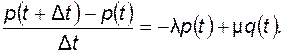
Устремляя D t ®0, имеем
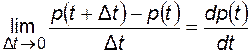 .
.
Следовательно, первое уравнение состояния будет выглядеть как
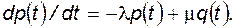 (4.30)
(4.30)
Проводя аналогичные рассуждения для второго состояния элемента – состояния отказа, можно получить второе уравнение состояния
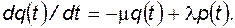 (4.31)
(4.31)
Таким образом, для описания вероятностей состояний элемента получена система из двух дифференциальных уравнений (4.30) и (4.31).
Если имеется направленный граф состояний элементов системы, то систему дифференциальных уравнений для вероятностей состояний 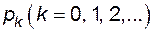 , можно сразу записать, пользуясь следующим простым правилом: в левой части каждого уравнения стоит производная
, можно сразу записать, пользуясь следующим простым правилом: в левой части каждого уравнения стоит производная 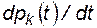 , а в правой – столько составляющих, сколько ребер графа состояний типа 4.2 и 4.3 связано непосредственно с данным состоянием; если ребро оканчивается в данном состоянии, то составляющая имеет знак плюс; если начинается из данного состояния - знак минус. Каждая составляющая равна произведению интенсивности потока событий, переводящего элемент или систему по данному ребру в другое состояние, на вероятность того состояния, из которого начинается ребро.
, а в правой – столько составляющих, сколько ребер графа состояний типа 4.2 и 4.3 связано непосредственно с данным состоянием; если ребро оканчивается в данном состоянии, то составляющая имеет знак плюс; если начинается из данного состояния - знак минус. Каждая составляющая равна произведению интенсивности потока событий, переводящего элемент или систему по данному ребру в другое состояние, на вероятность того состояния, из которого начинается ребро.
Решение системы уравнений, описывающих состояния одного элемента при начальных условиях 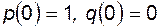 , дает вероятность безотказной работы
, дает вероятность безотказной работы
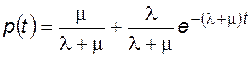 (4.32)
(4.32)
и вероятность отказа
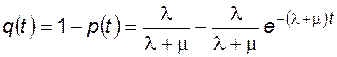 . (4.33)
. (4.33)
Если в начальный момент времени элемент находился в состоянии отказа, т.е. 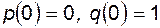 , то
, то
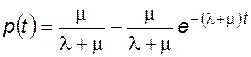 , (4.34)
, (4.34)
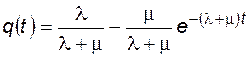 . (4.35)
. (4.35)
Для стационарного состояния 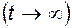 вероятность безотказной работы равна стационарному коэффициенту готовности, а вероятность отказа – коэффициенту неготовности (вынужденного простоя):
вероятность безотказной работы равна стационарному коэффициенту готовности, а вероятность отказа – коэффициенту неготовности (вынужденного простоя):
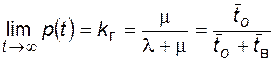 , (4.36)
, (4.36)
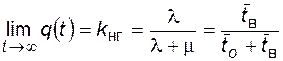 . (4.37)
. (4.37)
Для стационарных состояний марковские процессы вырождаются в марковские цепи.
Уравнения марковских процессов дают возможность вычислять как вероятности состояний (например, коэффициенты готовности и неготовности), так и вероятность наступления тех или иных событий (например, вероятность безотказной работы или отказа). В последнем случае искомое событие связывают с попаданием системы в поглощающее состояние.
Таким образом, метод, использующий марковские процессы, позволяет строго и в общем виде получать решения, т.е. вероятности всех состояний и их изменения во времени.
Однако этот метод ограничен только экспоненциальными моделями элементов, существенный недостаток метода – большая размерность матрицы состояний 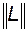 . Например, для системы, состоящей всего из 10 элементов, порядок матрицы равен
. Например, для системы, состоящей всего из 10 элементов, порядок матрицы равен 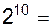 1024, что вызывает, с одной стороны, большие трудности в переборе всех состояний системы и определении коэффициентов перехода, а с другой - создает и большие вычислительные трудности.
1024, что вызывает, с одной стороны, большие трудности в переборе всех состояний системы и определении коэффициентов перехода, а с другой - создает и большие вычислительные трудности.
4.3.3.3. Аналитический логико-вероятностный метод. Такое название закрепилось за рассматриваемым методом, хотя любой метод расчета надежности содержит в себе и логическую и вероятностную части. Здесь же подразумевается, что метод основан на применении теорем теории вероятностей к функциям алгебры логики. Указанная основа метода предопределила принимаемые здесь допущения. В отличие от предыдущего метода предполагается, что не только элементы могут находиться в двух состояниях, но и сама система. Кроме того, этот метод в основном применим к системам, которые могут быть представлены сетевой структурой в смысле надежности.
Теоретически метод может быть применен к системе, времена безотказной работы и восстановлений элементов которой распределены по любому закону, однако практически он используется для систем с экспоненциально распределенными временами (с простейшим потоком отказов).
Таким образом, если структурно-функционально система описана функцией алгебры логики 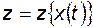 , то коэффициент готовности определяется как
, то коэффициент готовности определяется как
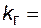 P
P 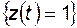 , (4.38)
, (4.38)
где 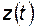 - функция работоспособности в момент времени t, а коэффициент неготовности
- функция работоспособности в момент времени t, а коэффициент неготовности
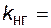 P
P 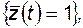 (4. 39)
(4. 39)
где 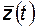 - функция неработосособности в момент времени t.
- функция неработосособности в момент времени t.
В качестве другого основного показателя можно определять вероятность безотказной работы на интервале времени 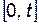 :
:
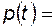 P
P 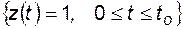 , (4.40)
, (4.40)
где 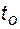 - время до отказа, а
- время до отказа, а 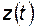 - функция работоспособности системы на интервале времени
- функция работоспособности системы на интервале времени 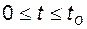 .
.
Различие между (4.38) и (4.40) заключается в том, что в первом случае функция работоспособности системы примет значение 1 в заданный момент времени t, а во втором случае функция работоспособности будет равна единице на интервале времени до отказа.
Основная проблема использования соотношений (4.38)- (4.40) состоит в том, что вероятностные показатели надежности системы зависят от вероятностных показателей состояний элементов.
В качестве примера определим вероятностные показатели надежности системы, состоящей из n последовательно соединенных в смысле надежности независимых элементов.
Функция работоспособности в момент времени t имеет вид
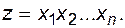
Коэффициент готовности
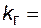 P
P 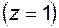 .
.
На основе теоремы умножения вероятностей имеем
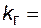 P (z = 1)=P
P (z = 1)=P 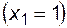 P
P 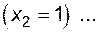 P
P 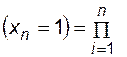
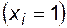 .
.
Поскольку P 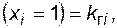 то
то
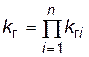 . (4.41)
. (4.41)
Коэффициент неготовности
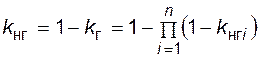 . (4.42)
. (4.42)
Если 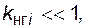 то
то
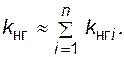 (4.43)
(4.43)
Ошибка последней формулы не превышает 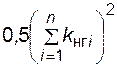 . Ее справедливость легко проверяется на численных примерах.
. Ее справедливость легко проверяется на численных примерах.
|
|
|
|
|
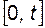 только при условии, что все ее элементы не откажут на этом интервале времени, то
только при условии, что все ее элементы не откажут на этом интервале времени, то
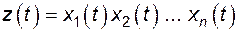 при
при 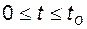 ;
;
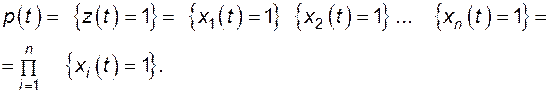
(4.44)
Но P 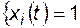 при
при 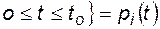 - вероятность безотказной работы i -го элемента, тогда
- вероятность безотказной работы i -го элемента, тогда
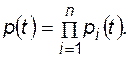 (4.45)
(4.45)
Если учесть (3.8), то
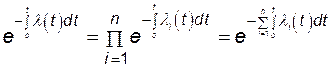 ,
,
откуда
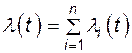 , (4.46)
, (4.46)
т.е. интенсивность отказов системы, состоящей из n последовательно соединенных в смысле надежности независимых элементов, равна сумме интенсивностей отказов ее элементов.
Если элементы с простейшими потоками отказов, то 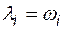 и
и
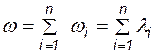 . (4.47)
. (4.47)
Аналогично вероятность отказа
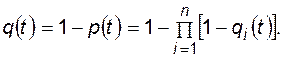 (4.48)
(4.48)
При 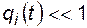
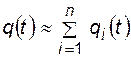 (4.49)
(4.49)
с ошибкой, не превышающей 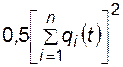 . Замечание о справедливости (4.49) то же, что и для (4.43).
. Замечание о справедливости (4.49) то же, что и для (4.43).
|
|
|
|
|
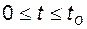 :
:
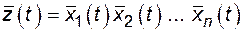 при
при 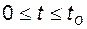 ;
;
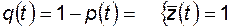 при
при 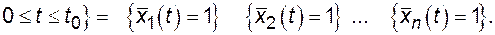
Но 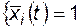 при
при 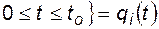 , следовательно,
, следовательно,
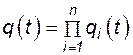 , (4.50)
, (4.50)
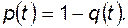 (4.51)
(4.51)
|
|
|
|
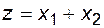 и неработоспособности
и неработоспособности 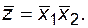
Коэффициент неготовности
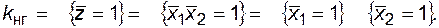
Но P 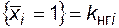 , следовательно,
, следовательно,
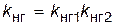 . (4.52)
. (4.52)
В случае n элементов коэффициент неготовности системы равен произведению коэффициентов неготовности элементов.
Соответственно коэффициент готовности для двух параллельно соединенных и восстанавливаемых элементов
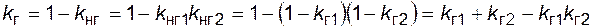 . (4.53)
. (4.53)
Определение вероятности безотказной работы системы для этого случая требует достаточно сложных выкладок и решения интегрального уравнения, поэтому здесь не рассматривается.
4.3.3.4. Аналитический метод на основе формулы полной вероятности. В случае сложной аварии может быть использован аналитический метод на основе формулы полной вероятности. При этом рассматриваются последствия отказов элементов системы в различных режимах с номерами j – нормальном, ремонтных и др. Наложения отказов элементов на режимы системы классифицируются как аварийные состояния с определенной степенью нарушения работоспособности системы: потеря генераторов, трансформаторов, линий, погашение секций шин, снижение располагаемой или выдаваемой мощности, дефицит мощности в системе, а также различные сочетания нарушений.
Аварии классифицируются по продолжительности ликвидации их последствий как кратковременные (оперативные переключения) и длительные (восстановительные ремонты). Последствия отказов устройств релейной защиты, противоаварийной автоматики и коммутационных аппаратов рассматриваются как развитие аварии.
Все элементы системы – генераторы, трансформаторы, линии, секции шин, выключатели, отделители, короткозамыкатели и др. – получают номера i. Для них задаются показатели надежности, например, 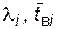 , и т.д. Для устройств релейной защиты и противоаварийной автоматики, коммутационной аппаратуры задаются их номера s, а также
, и т.д. Для устройств релейной защиты и противоаварийной автоматики, коммутационной аппаратуры задаются их номера s, а также 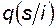 - условная вероятность отказа устройства с номером s при условии, что отказал элемент в основной схеме с номером i.
- условная вероятность отказа устройства с номером s при условии, что отказал элемент в основной схеме с номером i.
Плановые и аварийные режимы учитываются отдельно, если они отличаются составом отключенных элементов. Нормальный режим по полной схеме системы получает номер j = 0. Для каждого режима задаются показатели 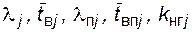 и др.
и др.
Все множество режимов составляет полную группу событий, поэтому в соответствии с формулой полной вероятности
|
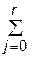 (4.54)
(4.54)
где r – число заданных режимов системы.
|
|
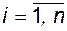 , формулой условной вероятности:
, формулой условной вероятности:
P 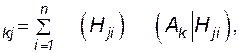 (4.55)
(4.55)
где P 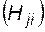 - вероятность отказа i -го элемента в j -м режиме;
- вероятность отказа i -го элемента в j -м режиме;
P 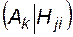 - вероятность возникновения аварии k -го вида при условии отказа i -го элемента в j -м режиме. Индекс i = 0 присвоим вероятности отсутствия отказов.
- вероятность возникновения аварии k -го вида при условии отказа i -го элемента в j -м режиме. Индекс i = 0 присвоим вероятности отсутствия отказов.
Если в случае отказа i -го элемента в j -м режиме происходит действие или отказ s -го комплекта релейной защиты, то по формуле условной вероятности
P 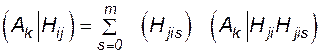 , (4.56)
, (4.56)
|
|
|
|
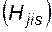 - вероятность отказа срабатывания s -го комплекта релейной защиты в случае отказа i -го элемента в j -м режиме. Индекс s = 0 отнесем к правильным действиям устройств релейной защиты; m – число устройств.
- вероятность отказа срабатывания s -го комплекта релейной защиты в случае отказа i -го элемента в j -м режиме. Индекс s = 0 отнесем к правильным действиям устройств релейной защиты; m – число устройств.
В случае отказа коммутационных аппаратов вероятность P 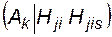 связана с вероятностью действий коммутационных аппаратов формулой условной вероятности
связана с вероятностью действий коммутационных аппаратов формулой условной вероятности
P 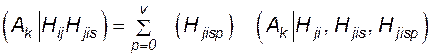 (4.57)
(4.57)
|
|
При учете действия устройств противоаварийной автоматики (АПВ, УРОВ, АВР и др.) также по формуле условной вероятности имеем
P 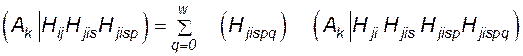 , (4.58)
, (4.58)
где q = 0 относится к безотказному действию устройств противоаварийной автоматики; w – число возможных отказов этих устройств. 
Таким образом могут быть получены вероятности различных аварийных ситуаций, возникающих в режиме j при отказе элемента i, последовавшем за ним отказе релейной защиты s, а далее отказе группы коммутационных аппаратов р и отказе противоаварийной автоматики q. Количество таких аварийных ситуаций определяется деревом развития аварии, когда на каждом этапе соответствующие устройства могут работать правильно или отказать.
Каждой из полученных аварийных ситуаций ставятся в соответствие ее последствия в виде, например, сохранения или нарушения питания потребителей, дефицита мощности, недоотпуска электроэнергии, ущерба и т.п. В результате получаем вероятностные характеристики последствий аварийных ситуаций в виде их частоты и/или глубины, и/или продолжительности и др.
4.3.3.5. Аналитический метод по схеме Бернулли. Часто приходится решать задачи по расчету показателей надежности, когда логическая часть либо весьма индивидуальна, либо крайне проста. Обычно в этих случаях логика укладывается в известные схемы: схема Бернулли или схема независимых испытаний, пуассоновский простейший поток и др.
Схема Бернулли предполагает проведение серии взаимно независимых испытаний, каждое из которых завершается успехом (в соответствии с заранее выбранным критерием) с вероятностью р или неудачей с дополнительной вероятностью q = 1 - p.
Для такой схемы можно определить вероятность того, что при n опытах успешными будут k из них, а (n - k) – неудачными:
P 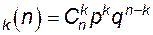 , (4.59)
, (4.59)
где 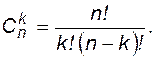
Если число успехов в n испытаниях обозначить величиной k, то эта величина случайная, а функция распределения ее будет 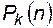 , которую называют биномиальной. Слово "биномиальное" отражает тот факт, что (4.59) представляет собой k -й член биномиального разложения
, которую называют биномиальной. Слово "биномиальное" отражает тот факт, что (4.59) представляет собой k -й член биномиального разложения
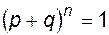 . (4.60)
. (4.60)
На основе схемы Бернулли можно решать многие задачи. Так, если полагать, что на подстанции работают n однотипных трансформаторов (т.е. имеем n испытаний), каждый из которых с вероятностью 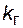 находится в работоспособном состоянии, а с вероятностью
находится в работоспособном состоянии, а с вероятностью 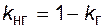 - в неработоспособном, то вероятность того, что в определенный момент окажутся работоспособными k трансформаторов, будет определяться формулой (4.59), где
- в неработоспособном, то вероятность того, что в определенный момент окажутся работоспособными k трансформаторов, будет определяться формулой (4.59), где 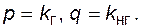
4.3.3.6. Аналитический метод на основе пуассоновского процесса. Пуассоновский процесс предполагает, что поток происходящих во времени событий обладает следующими свойствами:
· вероятность определенного количества событий пропорциональна длине интервала времени;
· вероятность двух и более событий за промежуток времени стремится к нулю, когда длительность этого промежутка времени стремится к нулю;
· количество событий, появляющихся на любых перекрещивающихся интервалах времени, независимо между собой.
Такой поток характеризуется параметром – среднее количество событий на интервале
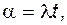 (4.61)
(4.61)
где l - частота появления события, l = w (см. (3.17)).
Для пуассоновского потока вероятность появления k событий на интервале времени t определяется как
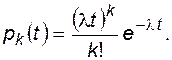 (4.62)
(4.62)
Например, если предположить, что поток отказов трансформатора на подстанции пуассоновский, то вероятность безотказной работы трансформатора будет
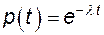 ,
,
что согласуется с ранее полученным выражением (3.17).
Если на подстанции n трансформаторов, то вероятность того, что на интервале времени t не откажет ни один из них,
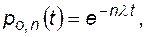 (4.63)
(4.63)
а вероятность того, что откажет один трансформатор из всех, -
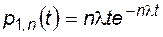 , (4.64)
, (4.64)
и т.д.
4.3.3.7. Имитационный метод. К огда невозможно при существующих средствах получить решение аналитическими методами или решение крайне сложное, громоздкое, применяют имитационное моделирование, основанное на компьютерном представлении процессов в системе. Основу имитационных методов составляет метод статистического моделирования (метод Монте-Карло).
Процесс статистического моделирования представляет собой процедуру многократного повторения определенных внешних условий и взаимодействий элементов системы. В результате каждого такого опыта формируется конкретная реализация исхода испытания. После серии опытов исследователь получает некоторую выборку случайных реализаций, которые затем подвергает стандартным процедурам статистической обработки.
Таким образом, в этом методе моделирование рассматривается как последовательность экспериментов. В ходе данных экспериментов моделируются события, причем происходят они в моменты, определяемые случайными процессами с заданными распределениями вероятностей.
Основные этапы такого исследования: построение формальной модели, программное обеспечение процесса имитации траекторий модели, имитационные эксперименты.
Этап построения формальной модели сводится к составлению алгоритма формирования необходимой последовательности событий, а также к определению траектории движения объекта, полученной на основе ее характеристик.
Этап организации программного обеспечения заключается в создании компьютерной программы, позволяющей воспроизвести (имитировать) траекторию модели в соответствии с имеющимися закономерностями и найти соответствующие показатели работы модели, а также в создании программ работы с моделью.
Этап организации имитационных экспериментов – это работа с моделью (выбор способа обработки выходной информации для эффективного получения необходимых результатов, получение выходных показателей надежности на основе выбранного способа и т.д.).
В итоге процесс функционирования системы представляется цепью изменения ее состояний 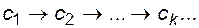 в случайные моменты времени
в случайные моменты времени 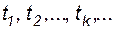
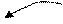
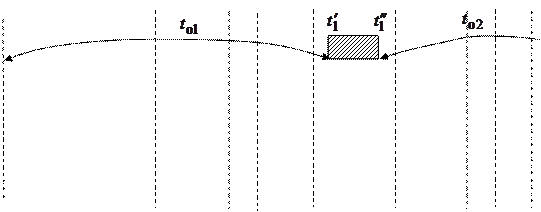
Схематически процесс функционирования для системы из n элементов показан на рис. 4.6, где приняты следующие обозначения: 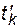 - момент k -го отказа элемента;
- момент k -го отказа элемента; 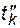 - момент окончания k -го восстановления элемента;
- момент окончания k -го восстановления элемента; 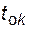 - интервал времени от момента (k- 1)-го восстановления до момента k -го отказа элемента;
- интервал времени от момента (k- 1)-го восстановления до момента k -го отказа элемента; 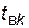 - интервал времени от момента (k -1)-го отказа до момента окончания k -го восстановления элемента. Указанные величины связаны между собой соотношениями:
- интервал времени от момента (k -1)-го отказа до момента окончания k -го восстановления элемента. Указанные величины связаны между собой соотношениями:
Интервалы времени 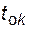 и
и 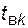 представляют собой отдельные реализации непрерывных случайных величин
представляют собой отдельные реализации непрерывных случайных величин 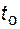 и
и 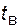 , характеризующих время исправной работы и время восстановления элемента системы. На компьютере организуется генерация потоков случайных чисел, подчиненных заданным законам распределения времени работы и времени восстановления элементов (обычно равномерное распределение). На основании этих чисел формируются моменты времени по формулам (4.65).
, характеризующих время исправной работы и время восстановления элемента системы. На компьютере организуется генерация потоков случайных чисел, подчиненных заданным законам распределения времени работы и времени восстановления элементов (обычно равномерное распределение). На основании этих чисел формируются моменты времени по формулам (4.65).
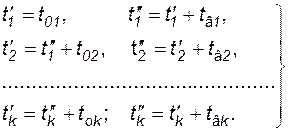 (4.65)
(4.65)
|
|
|
| ||||||||||
|
| ||||||||||||
| |||||||||||||



 Элемент
Элемент


|
|
|
|





 1
1
 | |||||||||||||
| |||||||||||||
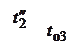 | |||||||||||||
| |||||||||||||
| |||||||||||||
| |||||||||||||
| |||||||||||||




|
 2
2





|
|
|
 i
i
 | |||
| |||



|
|
 n
n
 |
|
Рис. 4.6.
Пусть повторяются испытания системы N раз. При каждом испытании будут получаться новые случайные моменты отказов и восстановлений элементов системы. Если из N испытаний система отказала M раз (на рис. 4.6 отказ системы показан в результате наложения отказов элементов 1, 2 и I), то вероятность отказа системы за период t
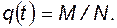 (4.66)
(4.66)
Частота отказов
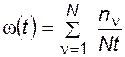 , (4.67)
, (4.67)
где 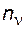 – число отказов системы при испытании n.
– число отказов системы при испытании n.
Аналогично можно вычислить и другие показатели надежности системы.
Отметим преимущества и недостатки метода статистических испытаний. Его преимущества: позволяет полнее учесть особенности функционирования сложной системы, в том числе с зависимыми элементами, а также любые законы распределения случайных величин, имеет наглядную вероятностную трактовку, малую чувствительность к случайным сбоям компью