Задачу определения последствий для потребителей при различных состояниях системы электроснабжения целесообразно рассматривать для двух случаев:
1) если пропускные способности элементов системы (линий, трансформаторов) не ограничивают передачу мощности от источников к узлам потребления в различных состояниях неполной работоспособности системы, а важно лишь наличие связей от источников к потребителям. Предполагается, что суммарная мощность источников электроэнергии достаточна, т.е. не меньше суммарной потребляемой мощности с учетом потерь в сети. Если мощности источников недостаточно для обеспечения нагрузки потребителей вследствие ее дефицита по каким-либо причинам, не зависящим от систем электроснабжения, например вследствие отказов источников электроэнергии, то потребители будут иметь соответствующие дефициты мощности и недоотпуски электроэнергии и, как следствие, экономические ущербы;
2) если пропускные способности элементов системы электроснабжения ограничивают передачу электроэнергии от источников к потребителям в некоторых состояниях системы при наличии связей между источниками и узлами нагрузки, то потребители будут иметь некоторые дефициты мощности продолжительностью, равной продолжительности этих состояний системы, и соответствующие недоотпуски электроэнергии, а следовательно, и экономические ущербы. При этом, как и в предыдущем случае, предполагается, что суммарная мощность источников электроэнергии не меньше суммарной мощности потребителей с учетом потерь в сети. Если в каких-то (или во всех) состояниях системы имеют место дефицит мощности источников электроэнергии и соответствующий ему недоотпуск электроэнергии, то эти дефицит и недоотпуск будут суммироваться с дефицитами и недоотпусками в результате ограниченной пропускной способности элементов.
Первый случай в контексте рассматриваемой задачи не представляет больше интереса. Что касается второго случая, то для определения последствий для потребителей при различных состояниях системы электроснабжения необходимо решать задачу потокораспределения.
Однако рассмотрим сначала причины, которые могут приводить к ограничению пропускной способности элементов системы электроснабжения. Таких причин две: а) ограничения по току, протекающему через элемент (линию, трансформатор), из условий нагрева проводников; б) ограничения по отклонениям напряжений, определяемые требованиями качества электроэнергии по уровням напряжений. Первое ограничение физически понятно. Второе связано с ситуацией, когда несмотря на предельно высокий уровень напряжения на отправной стороне элемента (в большей мере это относится к линиям, в меньшей мере – для трансформаторов) из-за потерь напряжения вследствие передачи большой мощности не удается обеспечить допустимый уровень напряжения на приемной стороне.
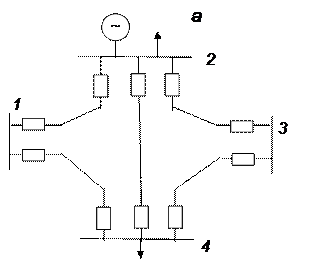
Дальнейшее изложение будем рассматривать на примере мостиковой схемы, представленной на рис. 4.4, внеся в нее для общности ситуации еще один источник электроэнергии в узле 2 (пусть это будет малая газотурбинная установка, относящаяся к разряду распределенной генерации). Модифицированная таким образом схема представлена на рис. 4.7, а.
 | |||
 | |||
Рис. 4.7
Ограничения пропускных способностей связей могут задаваться двумя способами: в виде неизменной предельной передаваемой по элементу мощности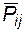 
(в некоторых случаях при передаче мощности в прямом и обратном направлениях могут иметь место разные пределы); путем задания предельных значений тока или/и напряжений. Первый способ приемлем, например, в случае относительно коротких линий, когда отклонения напряжений в различных режимах незначительны и ими можно пренебречь, а предельная пропускная способность элемента определяется током нагрева. Второй способ необходимо использовать в случае сравнительно длинных линий, когда отклонения напряжений в различных режимах существенны. Для этих двух случаев используются разные методы расчета потокораспределения в системе электроснабжения.
При задании предельных пропускных способностей связей предельной передаваемой мощностью 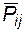расчет потокораспределения в схеме может быть выполнен с использованием так называемых потоковых алгоритмов. Один из наиболее распространенных и в то же время наиболее простых – это алгоритм Форда-Фалкерсона. Поясним его на примере схемы рис. 4.7, а, которая при этом преобразуется в расширенную схему рис. 4.7, б, где введены два дополнительных узла – u (в него перенесены и просуммированы все мощности источников) и n (в него перенесены и просуммированы все мощности нагрузок). Пропускная способность каждой новой связи, соединяющей узел исходной схемы с узлом u или n, задается равной переносимой мощности источника или нагрузки. В этом случае дополнительные связи не ограничивают передачу мощности от агрегированного источника (узел u) к агрегированному потребителю (узел n) и потокораспределение в расширенной схеме не будет отличаться от потокораспределения в исходной схеме.
Задача потокораспределения решается путем нахождения минимального сечения расширенной схемы, которое и ограничивает передачу мощности от источников к потребителям, если суммарная пропускная способность его меньше суммарной мощности потребителей в системе. В данном случае минимальное сечение – это сечение с минимальной суммарной пропускной способностью входящих в него связей. Тем самым оно отличается от понятия минимального сечения, введенного в п. 4.3.2.2 и определяемого лишь топологией схемы сети. Минимальное сечение расширенной схемы можно найти перебором всех сечений (комбинаторным методом) или другими методами.
Если пропускная способность минимального сечения больше или равна суммарной потребляемой мощности, то очевидно, что схема исходной сети в рассматриваемом состоянии не ограничивает передачу мощности от источников электроэнергии к потребителям.
Когда ограничения по пропускной способности связей определяются на основе предельных токов и напряжений, необходим расчет установившегося электрического режима системы электроснабжения. В общем случае такой расчет базируется на решении нелинейных систем алгебраических уравнений, в основу которых положены уравнения узловых напряжений или контурных токов. Наиболее распространенным представлением электрической сети являются уравнения узловых напряжений. Могут быть учтены статические характеристики нагрузок по напряжению. Система нелинейных алгебраических уравнений при расчете электрического режима решается обычно итерационным методом Ньютона или его модификациями. При этом на каждой итерации получающаяся система линейных алгебраических уравнений решается методом исключения Гаусса.
В результате расчета электрического режима схемы системы электроснабжения получаем токи в связях и напряжения в узлах схемы. Если получаемые токи и напряжения не укладываются в заданные ограничения, определяемые предельными токами и напряжениями, необходимо изменять потокораспределение, например путем уменьшения нагрузок. Поиск минимально необходимого уменьшения нагрузок (ограничения) потребителей – это оптимизационная задача, которую можно решить тем или иным методом математического программирования (градиентным, ветвей и границ и др.).
В случае радиальной (незамкнутой) схемы системы электроснабжения задача потокораспределения и поиск минимально необходимого уменьшения нагрузок (ограничения) потребителей для получения допустимого режима существенно упрощаются.
Если в системе электроснабжения имеются средства регулирования режима (например, регулируемые источники реактивной мощности, трансформаторы с поперечным регулированием, гибкие электропередачи переменного тока – FACTS, распределенная генерация и др.), тогда ограничения потребителей в рассматриваемом состоянии системы можно уменьшить изменением потокораспределения и уровней напряжений c использованием средств регулирования режима. Соответствующая задача также является оптимизационной и в условиях эксплуатации направлена на выбор таких параметров установленных регулирующих устройств, которые приводили бы к минимальному ограничению потребителей в этом состоянии системы. На уровне проектирования системы электроснабжения подобная задача заключается в оптимальном выборе мощности и мест установки регулирующих устройств.
Примеры и задачи
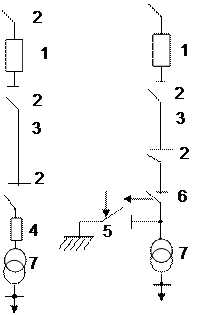
4.3.5.1. На рис. 4.8 приведены схемы питания однотрансформаторных подстанций 110 кВ. Отказ системы электроснабжения таких подстанций вызывается отказом любого из элементов. Частота отказов элементов: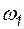 
= 0,02; 
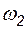= 0,01; 
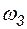= 1,0; 
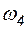= 0,02; 
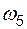= 0,01; 
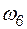= 0,01; 
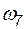= 0,01 1/год. В соответствии с формулой (4.47) получим варианты оценки частоты погашения подстанции:
а б в г д
 | |||||||
 | |||||||
 | |||||||
 | |||||||
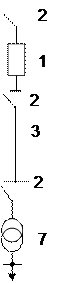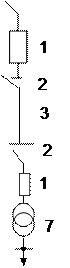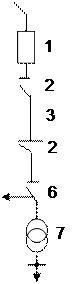Рис. 4.8.
а)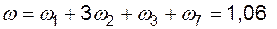 
1/год;
б)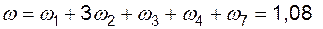 
1/год;
в)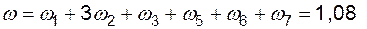 
1/год;
г)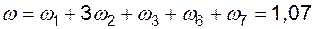 
1/год;
д)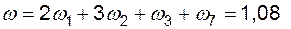 
1/год;
Эти результаты показывают, что доминирующее влияние на частоту погашения подстанции оказывает повреждаемость воздушных линий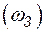 
.
4.3.5.2. Рассмотрим секцию РУ 6 кВ, от которой питается 21 отходящая линия (рис. 4.9). Частота отказов с коротким замыканием для выключателей 6 кВ оценивается как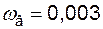 
1/год; для сборных шин – как 
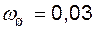1/год. Тогда частота кратковременных погашений секций 6 кВ из-за коротких замыканий на шинах и на выключателях составит 
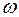= 22 
+ 
= 22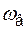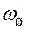×0,003 + 0,03 = 0,096 1/год.
Таким образом, частота погашений секции 6 кВ определяется в основном числом присоединений и надежностью выключателей
1 2 3 21
Рис. 4.9.
4.3.5.3. Потребитель питается от двух независимых источников по схеме, приведенной на рис. 4.10. Один источник (основной, рабочий) включен постоянно (выключатель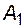 
), другой включается действием АВР (выключатель 
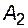). Вероятность безотказной работы источника в течение времени между плановыми его остановами 0,9. Вероятность застать резервный источник в работоспособном состоянии в любой момент времени между плановыми остановами основного источника равна 0,99, вероятность отказа выключателя в отключении - 0,05 и во включении – 0,01. Определим вероятность безотказной работы системы электроснабжения в течение времени между плановыми остановами основного источника с учетом возможности использования резервного источника, считая, что вероятностью его отказа за время восстановления рабочего источника можно пренебречь.
Решение. В соответствии с условиями данного примера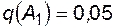 
; 
; 
; 
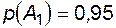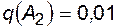При резервировании замещением вероятность отказа системы будет определяться по формуле полной вероятности
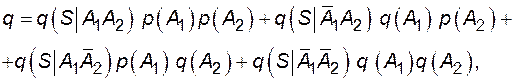
где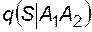 
условная вероятность отказа системы при отсутствии отказов выключателей; 
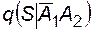- то же при отказе в отключении отказавшего источника; 
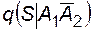- то же при отказе во включении резервного источника; 
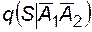- то же при совпадении отказа в отключении с отказом во включении; 
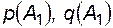- вероятности отсутствия отказа и отказа в отключении;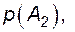 
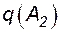- вероятность отсутствия отказа и отказа во включении.
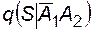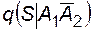Очевидно, что = 1; = 1; 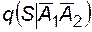= 1. Вероятность отказа системы при отсутствии отказов выключателей определяется вероятностью аварийного простоя резервного источника: 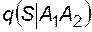= (1-0,99) = 0,01, поскольку при отказе рабочего источника выключатель его отключает. Тогда по приведенной формуле q = 0,01×0,99×0,95 + 1×0,05×0,99 + 1×0,95×0,01 + 1×0,05×0,01 = 0,0689.
В соответствии с (4.37) для стационарного состояния случайного процесса отказов-восстановлений вероятность отказа в относительных единицах эквивалентна коэффициенту неготовности и равна отношению времени нахождения объекта в неработоспособном состоянии (времени восстановления работоспособности) к суммарному времени работоспособного и неработоспособного состояний объекта. Если в качестве последнего рассматривать, например, 1 год, то найденные значения q = 0,0689 отражает долю года, в течение которой объект – система – будет находиться в неработоспособном состоянии, а потребитель не будет получать электроэнергию. Если подсчитать эту долю года, например, в часах, то это будет 0,0689∙8760 ≈ 603 ч.
Можно иначе интерпретировать полученную вероятность q. Ее значение условно означает, что, например, в течение года произойдет 0,0689 отказов. Если задаться целью определить, в течение какого периода (за сколько лет) будет происходить один отказ, то получим 1/0,0689 ≈ 14,5, т.е. один отказ в 14,5 лет.
Использование таких интерпретаций вероятностей отказа часто оправдано практически, поскольку вероятность – это несколько "абстрактное" понятие, т.е. бывает трудно сделать вывод, вероятность отказа в 6 % – это хороший уровень надежности или не очень. В то же время измерение в часах за год или "один отказ в какое-то число лет" в определенном смысле более "физично" и легче воспринимается и оценивается.
 |
Рис. 4.10. Рис. 4.11.
4.3.5.4. Потребители могут быть подключены к двум различным секциям шин (рис. 4.11). Вероятности отказа источников и выключателей те же, что и в примере 4.3.5.3. Различие схемы рис. 4.10 и 4.11 заключается в работе выключателей: на рис. 4.11 секционный выключатель осуществляет АВР секции, оставшейся без питания, за счет соседней секции и ее источника. Определим вероятность бесперебойного электроснабжения любого из потребителей этой системы.
Решение. В соответствии с условиями примера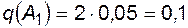 
; 
; ; 
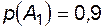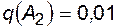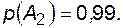Каждый из потребителей может оказаться подсоединенным к одной из секций с вероятностью 0,5, поэтому 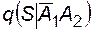= 0,5; 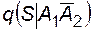= = 0,5; 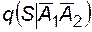= 0,5.
При отсутствии отказов выключателей отказ системы происходит при совпадении отказа одного из источников с аварийным простоем другого, т.е. 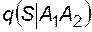= 2(1-0,9)(1-0,99) = 0,002.
По формуле полной вероятности получим q = 0,002×0,9×0,99 + + 0,5×0,1×0,99 + 0,5×0,9×0,01 + 0,5×0,1×0,01 = 0,05628. Искомая вероятность р = 1-0,05628 = 0,94372.
По аналогии с задачей 4.3.5.3 вероятность отказа в электроснабжении любого из потребителей схемы на рис. 4.11 в числе часов в году будет 0,05628∙8760 ≈ 493 ч. Также 1/0,05628 ≈ 17,8, т.е. один отказ в 17,8 лет.
4.3.5.5. Потребитель получает питание по линиям электропередачи от двух источников. Коэффициенты готовности этих линий соответственно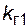 
= 0,998 и 
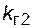= 0,995. Каждая линия еще простаивает в плановых ремонтах с относительной длительностью 
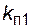= 0,02 и 
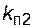= 0,03. Определить относительную длительность аварийного простоя потребителя.
Решение. Воспользуемся формулой полной вероятности. Сформируем полную группу несовместных: событие 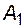- плановый ремонт первой линии; 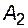- плановый ремонт второй линии; 
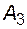- в рассматриваемой системе нет плановых ремонтов. Вероятность первого события - 
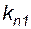, второго - 
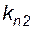(события несовместимы), вероятность третьего – (1- 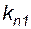- 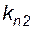). При первом состоянии системы (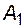) потребитель окажется в отключенном состоянии с вероятностью (1– 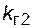), при втором (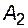) - с вероятностью (1- 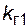), при третьем (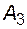) - с вероятностью 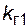(1– ) (1– 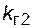). Следовательно, полная вероятность для потребителя оказаться в отключенном состоянии будет
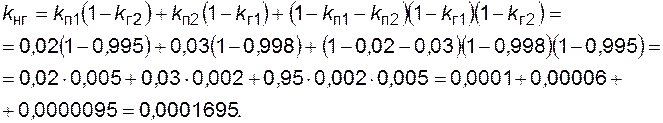
Аналогично предыдущим двум задачам потребитель не будет получать электроэнергию 1,48 ч в году, или будет происходить один отказ в электроснабжении за 5900 лет. Видно, что рассмотренная система электроснабжения весьма надежна.
4.3.5.6. Рассмотрим типовую схему питания секции BV 6 кВ собственных нужд, предназначенной для электроснабжения механизмов, которые обеспечивают безопасность АЭС (рис. 4.12). На рис. 4.12 даны следующие обозначения: ТСН - трансформатор собственных нужд; РТСН – резервный трансформатор собственных нужд; ДГ – двигатель-генератор; МРП – магистраль резервного питания; ОРУ – открытое распредустройство; Т – трансформатор; Г – генератор.
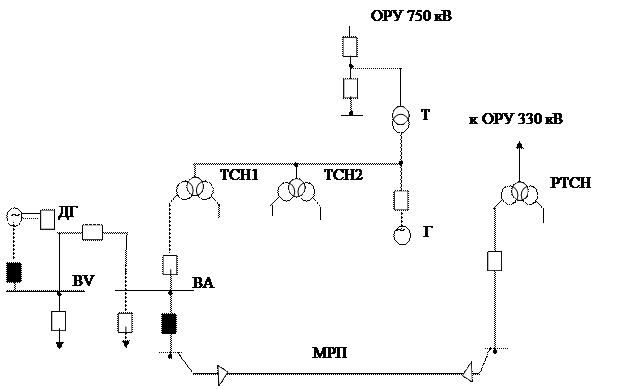
Рис. 4.12.
Дерево отказов для оценки частоты потери системного питания секции BV приведено на рис. 4.13. Функцию отказа для потери системного питания запишем так:
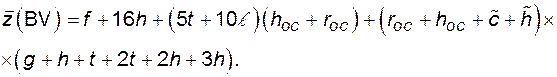
Здесь имеется ввиду, что к секции ВА присоединено 10 электродвигателей и 5 трансформаторов.
               |
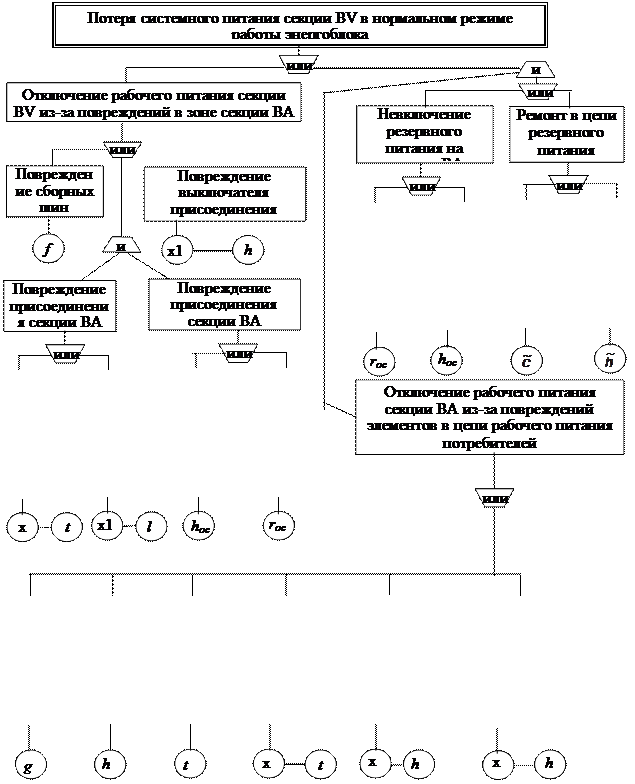Рис. 4.13.
Формула для частоты отключений от системного питания будет иметь следующий вид:
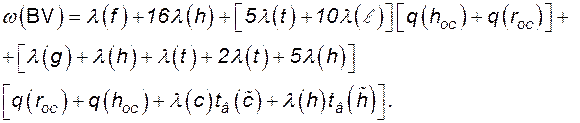
В табл. 4.3 и 4.4 приведены необходимые исходные данные. Подставив исходные данные, получим
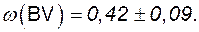
Т а б л и ц а 4.3
Показатели надежности элементов системы
электроснабжения
| Код | Наименование | l, год-1 | t в, год |
| с f g l t | Кабельная линия 6 кВ Секция шин 6 кВ Двигатель-генератор Двигатель нагрузки 6 кВ Трансформатор собственных нужд: рабочий резервный | (5,0±2,0) ×10-3 (3,0±1,0) ×10-2 (2,0±0,5) ×10-2 (1,0±0,5) ×10-1 (1,2±0,5) ×10-2 (5,0±4,0) ×10-3 | (1,0±0,5) ×10-3 (1,0±0,5) ×10-3 (1,0±0,5) ×10-2 (2,0±0,5) ×10-3 (5,0±0,2) ×10-3 (1,0±0,2) ×10-2 |
Т а б л и ц а 4.4
Отказ в системе автоматического управления
электроснабжением
| Код | Описание | Условная вероятность |
| h oc r oc g oc | Отказ масляного выключателя 6 кВ: во включении в отключении короткого замыкания Отказ срабатывания: устройства АВР устройства релейной защиты Отказ двигателя-генератора при пуске | (2,2±1,0)×10-3 (2,7±1,0)×10-2 (1,0±0,5)×10-2 (1,0±0,5)×10-3 (1,0±0,5)×10-2 |
При отключении секции BV от секции ВА запускается двигатель-генератор. Вероятность его отказа при пуске равна 0,01 (см. табл. 4.4). Погашение секции BV является следствием совпадения двух событий: отключения от системного питания и незапуска двигателя-генератора. Следовательно, частота погашений секции BV, пренебрегая разбросом показателей надежности, будет равна 0,42×0,01 = 0,004 год-1, т.е. погашение возможно не более 1 раза в 250 лет.
4.3.5.7. Определить среднегодовой недоотпуск электроэнергии потребителю, схема электроснабжения которого приведена на рис. 4.14. При этом пропускные способности ВЛ1 и ВЛ2 равны
~
| |||||
| |||||
 | |||||
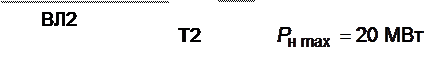Рис. 4.14.
20 МВт каждая, коэффициенты готовности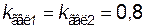 
. Мощность трансформаторов 25 МВА каждый, коэффициенты готовности 
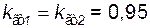. Суточный график нагрузки одинаковый в течение года и характеризуется тем, что с 0 до 8 ч и с 20 до 24 ч нагрузка равна 0,75 
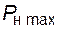, а с 8 до 20 ч – 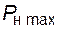. Система имеет 100 %-ную надежность.
Очевидно, что расчетная схема по надежности будет топологически идентична рис. 4.14.
Используя (4.41) для последовательно соединенных элементов и (4.53) для параллельно соединенных, запишем формулу для определения коэффициента готовности схемы. Подставив их значения, получим
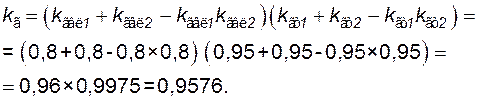
Соответственно коэффициент неготовности схемы
.
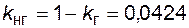Из характеристик суточного графика нагрузки видно, что 12 ч она составляет 0,75 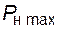и 12 ч – 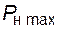. Поэтому математическое ожидание среднегодового недоотпуска электроэнергии определится как
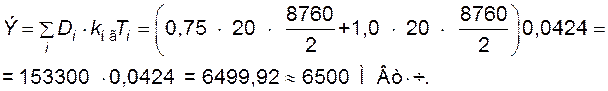
4.3.5.8. Определим надежность (вероятность (коэффициент готовности) и длительность) электроснабжения потребителя, снабжаемого от дизельной электростанции (ДЭС) с тремя агрегатами по рис. 4.15. Мощность одного агрегата ДЭС равна 500 кВт, коэффициент готовности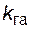 
= 0,9. Воздушная линия имеет длину 0,5 км с пропускной способностью 1500 кВт, удельная аварийность ВЛ 
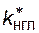= 0,01 1/км. Нагрузка равна 1500 кВт.
|
|
~
|
~
|
Данная схема содержит три агрегата ДЭС, включенные по надежности параллельно.
Используем сначала аналог формулы (4.52) для трех параллельно соединенных элементов. Получим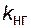 
= 0,1∙0,1∙0,1 = 0,001. Коэффициент готовности будет 
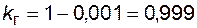. Определим 
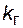иначе. Формула (4.53) была получена для двух параллельно соединенных элементов. Поэтому используем формулу (4.53) дважды: сначала для двух агрегатов из трех, а затем для полученного эквивалентного агрегата и оставшегося исходного (также для двух):
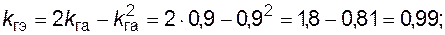
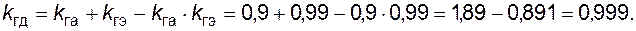
Далее по формуле (4.41) найдем коэффициент готовности схемы в целом
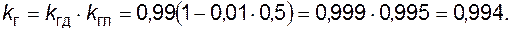
Длительность надежного электроснабжения потребителя будет равна
8760∙0,994 = 8707 ч/год.
Таким образом, потребитель не получит электроэнергию всего 53 часа в год, т.е. надежность его электроснабжения достаточно высока.