Методы расчета показателей

 

Различают точечные и интервальные оценки показателей надежности.

Точечная оценка показателей. Расчетные выражения для точечных оценок показателей надежности объекта могут быть экспериментальными методами оценены следующим образом (оцениваемые показатели обозначены с "крышечкой" сверху).

Вероятность безотказной работы

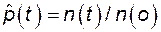, (4.1)

где n (o) – число наблюдаемых объектов в начале эксперимента; n (t) – число оставшихся работоспособных объектов в момент времени t (объекты невосстанавливаемые).

Интенсивность отказа в момент времени t

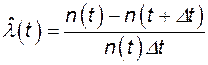, (4.2)

где D t – небольшой интервал времени.

Средняя наработка до отказа для случая отсутствия замены или восстановления объектов

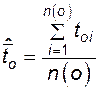, (4.3)

где 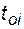- время до отказа i -го наблюдаемого объекта.

Частота отказов на интервале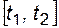

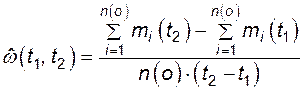, (4.4)

где 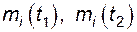- число отказов i -го объекта до момента времен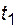и и 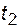соответственно.

Интенсивность восстановления

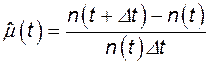, (4.5)

где 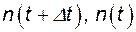- число объектов, восстановление которых длилось меньше t +D t и t соответственно.

Коэффициент готовности

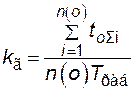, (4.6)

где 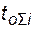– суммарное время пребывания i -го объекта в работоспособном состоянии за время 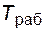; 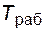– продолжительность наблюдения, включающая интервалы работоспособного состояния и ремонтов после отказов.

Если времена 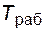различны для каждого из наблюдаемых объектов, то

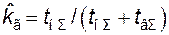, (4.7)

где 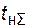– суммарная наработка всех объектов; 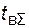- суммарное время восстановления после отказов.

Или

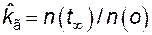, (4.8)

где 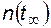– число объектов, находящихся в состоянии работоспособности в произвольный "достаточно удаленный" момент времени.

Коэффициент технического использования

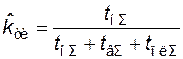, (4.9)

где 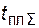– суммарное время плановых ремонтов.

Интервальная оценка показателей. Любая полученная точечная оценка, если даже она удовлетворяет всем критериям качества, обладает существенным недостатком в том смысле, что сама представляет собой лишь частное значение случайной величины. Поэтому кроме точечной оценки желательно знать практически надежные границы для оцениваемого параметра, т.е. найти такой интервал оценок, который с достаточно высокой вероятностью "накрывает" неизвестный параметр.

Очевидно, что достоверными границами для показателей надежности (абсолютно надежными границами) являются для 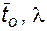и других аналогичных показателей – [0, ¥], для p (t), 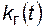и других вероятностей – [0, 1]. Указание других границ сопряжено с риском совершить ошибку. Вероятности ошибок 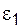и 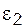называют уровнями зависимости оценок: 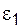– вероятность того, что найденный интервал не накроет используемый параметр своим левым концом; 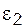– вероятность того, что найденный интервал не накроет используемый параметр своим правым концом.

За меру достоверности оценки – доверительной вероятности – принимается величина 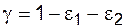, показывающая, с какой вероятностью можно утверждать, что доверительный интервал "накроет" истинное значение показателя,

g = P 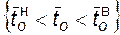, (4.10)

где 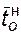, 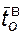– нижняя и верхняя границы доверительного интервала соответственно для показателя "среднее время до отказа".

Чаще всего вероятност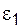и и 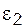выбираются одинаковыми, тогда g =1 - 2e и, следовательно, каждая из доверительных границ определяется с уровнем значимости e = 1 - g/2 или с односторонней доверительной вероятностью (коэффициентом доверия)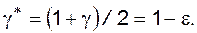

Если известен вид функции распределения оценки, то принцип вычисления доверительных интервалов состоит в том, что за нижнюю и верхнюю доверительные границы принимаются квантили этого распределения по соответствующему уровню. Нижняя доверительная граница определяется как квантиль по уровню e, а верхняя – как квантиль по уровню 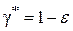. Вид распределения оценки зависит, в свою очередь, от вида распределения исследуемой случайной величины и тех функциональных преобразований, которые производятся над исходной статистикой при получении оценок.

 

Примеры и задачи

 

4 2.6.1. На испытание поставлено 1000 однотипных ламп. За 3000 ч отказало 80 ламп, а за интервал от 3000 до 4000 ч отказало еще 50 ламп. Определить вероятность безотказной работы 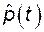, вероятность отказа 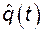для t = 3000 ч, 4000 ч и интенсивность отказов 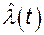для t = 3000 ч.

Решение.

Вероятность безотказной работы и отказа

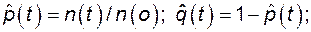
р (3000) = (1000-80)/1000 = 0,92; ;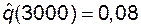

р (4000) = (1000-130)/1000 = 0,87; .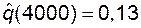

Интенсивность отказов

;

.

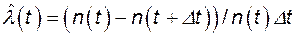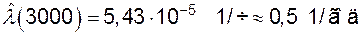4.2.6.2. Общее количество изоляторов воздушных линий сетевого участка 200 000 шт. Наблюдение показало, что из взятых под наблюдение в начале года изоляторов в первом квартале вышли из строя 4000, во втором – 3000, в третьем – 2000, в четвертом – 1000. Рассчитать по этим данным и построить характеристику безотказности .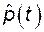

4.2.6.3. В аварийно-восстановительном ремонте находятся 15 однотипных масляных выключателей. Статистика восстановительных ремонтов такова:

 

t
n (t)

 

Определить статистические значения интенсивности восстановления на каждом интервале, среднюю продолжительность восстановления, среднюю интенсивность восстановления.

 

4.2.6.4. За наблюдаемый период эксплуатации участка системы электроснабжения было зафиксировано семь отказов. Время восстановления составило 8,2; 7; 8,4; 8,6; 7,4; 8; 7,9 ч соответственно. Определить среднее время восстановления системы.

 

Расчетные методы

 

Общий случай

 

Как уже отмечалось, эти методы применяются тогда, когда анализируется надежность объекта, представленного в виде системы, об элементах и связях которой известна вся информация (показатели надежности элементов, структура и функциональное взаимодействие их и т.д.).

Первоначально методы расчета разрабатывались для решения конкретных практических задач. Многообразие реальных задач и объектов породило множество различных методов, которые учитывали ту или иную специфику этих задач, объектов.

Определенная унификация этого множества методов стала возможной только за счет абстрагирования от специфики тех или иных задач, специфики объектов и построения модели некоторого абстрактного объекта. В итоге такой абстрактный объект представляет собой систему, состоящую из n элементов, функционально связанных между собой в общем случае любым необходимым способом, обеспечивающим выполнение объектом его функций, т.е. преобразование "входа" в "выход" (рис. 4.1). Для систем электроснабжения "входом" является, например, суммарная мощность питающих источников, изменяющаяся на рассматриваемом интервале времени в соответствии с заданным законом, а "выходом" – суммарная нагрузка на это же интервале, изменяющаяся в соответствии с суммарным графиком.

 

Система

...

"Выход"

"Вход"

 

...

 

........................

 

 

Рис. 4.1.

 

Каждый i -й элемент системы в общем случае может находиться в смысле надежности в 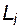состояниях. Тогда объект-система может находиться в 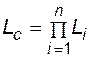состояниях.

Отказы и состояния элементов в общем случае могут быть зависимыми. Потоки отказов и восстановлений элементов в общем случае могут быть любыми (нестационарными, с последствиями или простейшими).

Задача состоит в выявлении состояний объекта-системы и событий перехода в состояния, обусловливающих изменение уровня работоспособности объекта, а также вероятностные характеристики этих состояний и событий.

Решение такой задачи представляет большую методическую трудность. Поэтому реально разработанные методы имеют ряд допущений. Практически все они рассматривают объекты-систе-мы, элементы которых могут находиться только в двух состояниях – работоспособном и неработоспособном. Часть методов упрощает задачу при условии, что и сам объект-система имеет два состояния (точнее все множество состояний 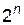разбивается на два подмножества). Другая группа методов упрощает задачу в предположении, что потоки отказов и восстановлений являются простейшими. Далее все эти упрощения раскрываются при рассмотрении конкретных методов.

Как было отмечено, в общем случае задача состоит из двух подзадач: 1) выявление состояний системы и событий перехода в эти состояния; 2) определение вероятностных характеристик этих состояний и событий.

Особенности первой подзадачи определяются спецификой рассматриваемой системы. Наиболее простым для систем электроснабжения является случай, когда в любых состояниях системы не проявляются ограничения по пропускной способности элементов. Такая ситуация, как правило, может быть справедливой, например, при анализе надежности схемы соединений подстанции. В других случаях ограничения по пропускной способности элементов системы электроснабжения могут не сказываться при наиболее вероятных состояниях системы (например, при совпадении отказов на не более чем двух линиях, принимая, что совпадение более двух отказов на линиях – это весьма маловероятное событие, которым можно пренебречь). Методы определения состояний системы по состояниям элементов на уровне структурно-функциональных показателей рассматриваются в п. 4.3.2.

Однако во многих ситуациях для систем электроснабжения в некоторых состояниях неполной работоспособности системы ограничения по пропускной способности элементов сказываются на возможности передачи мощности от источников ("входов") к потребителям ("выходам"). Тогда приходится решать задачу потокораспределения в системе электроснабжения для таких состояний с ограничениями передачи мощности, оценивать возникающие дефициты и недоотпуски электроэнергии потребителям. Методы определения последствий для потребителей в таких состояниях путем расчета потокораспределения рассматриваются в п. 4.3.4.

Методы решения второй подзадачи – определения вероятностных характеристик состояний системы в зависимости от состояний элементов и событий перехода системы в эти состояния – изложены в п. 4.3.3.