Применение фильтра Калмана в задаче измерения уровня и плотности жидкости с помощью двух датчиков давления
А.Л. Шестаков, А.С. Семенов, И.Г. Корепанов, О.Л. Ибряева
Application of Kalman filter to the problem of liquid level and density measuring by means of two pressure sensors
A.L. Shestakov, A.S. Semenov, I.G. Korepanov, O.L. Ibryaeva
Задача контроля уровня рабочей среды является одной из самых распространенных в системах управления технологическими процессами [1, 2]. Большое разнообразие физико-химических свойств контролируемых жидкостей определяет необходимость использования различных типов датчиков уровня. Наибольшее распространение получили датчики поплавкового типа и высокочастотные коаксиальные датчики. Однако каждый тип датчиков имеет свои ограничения и недостатки.
Существенный недостаток датчиков поплавкового типа заключается в том, что возможно заклинивание поплавка, ведущее к нарушению работы датчика. Высокочастотные же датчики могут работать лишь с электропроводящими жидкостями. В связи с этим возникает стремление рассмотреть другие типы датчиков, имеющих достаточно простой принцип работы и не имеющих ограничений, свойственных используемым.
Решение о возможности использования того или иного типа датчиков в условиях реального технологического процесса может приниматься лишь после тщательного исследования как конструктивных особенностей датчика, так и последствий воздействия на него дестабилизирующих факторов рабочей среды. Исходя из общетехнического принципа — чем проще устройство, тем оно надежнее, а также учитывая экономические аспекты, мы считаем, что особый интерес представляет исследование гидростатических датчиков уровня, как устройств, имеющих максимально простую конструкцию. Принцип действия гидростатического датчика основан на пропорциональной зависимости давления столба жидкости от его высоты. Кроме того, давление столба жидкости зависит от ее плотности, которую во многих случаях тоже следует считать переменной.
Постановка задачи: измерение уровня и плотности жидкости с помощью двух датчиков давления.
Используется два датчика давления, расположенных в жидкости на разных высотах. Назовем иx датчик 1 и датчик 2, и пусть датчик 1 расположен на дне резервуара, а датчик 2 – на 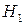 выше датчика 1.
выше датчика 1.
Задача, которой посвящена эта статья, такова: по данным двух датчиков давления отслеживать в режиме реального времени и с максимальной точностью изменения уровня и плотности жидкости.
Помимо полезного сигнала, на выходе датчиков неизбежно присутствует шум, вызванный различными факторами, в том числе и случайными погрешностями измерения, присущими самим датчикам. Чтобы восстановить, насколько возможно, полезный сигнал, мы отфильтровываем шум с помощью рекуррентного алгоритма, основанного на фильтре Калмана [3]. Это находится в русле современной тенденции, связанной с «интеллектуализацией» датчиков: в вопросах обеспечения необходимой точности преобладающую роль начинают играть программно-алгоритмические, а не аппаратные средства [4].
Описание технологического процесса и процесса измерения линейными стохастическими уравнениями.
1. Связи между переменными в отсутствие шумов.
Мы будем обозначать данные датчика давления 1 буквой 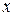 , а данные датчика давления 2 (верхнего) — буквой
, а данные датчика давления 2 (верхнего) — буквой 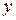 . Если бы не существовало ошибок измерения, и если бы жидкость в емкости находилась в идеальном покое, то превышение уровня жидкости над вторым датчиком
. Если бы не существовало ошибок измерения, и если бы жидкость в емкости находилась в идеальном покое, то превышение уровня жидкости над вторым датчиком 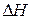 и плотность
и плотность 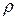 можно было бы найти по этим данным согласно формулам
можно было бы найти по этим данным согласно формулам
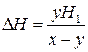 ,
, 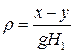 . (1)
. (1)
Хотя в этом пункте мы выписываем формулы в предположении отсутствия шумов, мы имеем в виду нашу цель — исследовать возможность восстановления величин 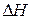 и
и 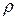 по данным
по данным 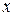 и
и 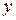 в условиях шумов и возмущений с применением рекуррентного алгоритма фильтра Калмана.
в условиях шумов и возмущений с применением рекуррентного алгоритма фильтра Калмана.
Первая из формул (1) имеет нелинейный характер, в то время как применение фильтра Калмана значительно упрощается как в принципиальном, так и в вычислительном плане, если все зависимости имеют линейный характер. В нашей задаче нетрудно перейти к линейным зависимостям, если заменить пару переменных 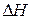 и
и 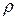 на новую пару
на новую пару 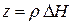 и
и 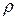 . Имеем:
. Имеем:
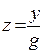 ,
, 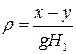 . (2)
. (2)
Заметим, что переход к переменной 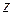 представляется осмысленным не только с точки зрения упрощения формул. В предположении постоянства площади горизонтального сечения емкости
представляется осмысленным не только с точки зрения упрощения формул. В предположении постоянства площади горизонтального сечения емкости 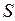 величина
величина 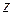 пропорциональна массе
пропорциональна массе 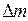 жидкости, находящейся над вторым датчиком:
жидкости, находящейся над вторым датчиком:
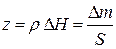 .
.
Обратные к выражениям (2) зависимости — выражения измеряемых величин 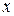 и
и 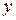 через
через 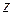 и
и 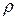 — являются, разумеется, тоже линейными. В условиях отсутствия шумов их можно следующим образом записать в матричном виде:
— являются, разумеется, тоже линейными. В условиях отсутствия шумов их можно следующим образом записать в матричном виде:
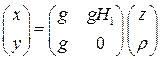 . (3)
. (3)
2. Стохастические уравнения, описывающие ход технологического процесса.
Использование фильтра Калмана предполагает, что изучаемый процесс с разумной степенью точности описывается стохастическими дифференциальными или разностными уравнениями. Эти уравнения обычно отражают общие представления о «типичном» ходе процесса, отклонения от которого считаются случайными и описываются с помощью «шумов». Будем считать, что типичное поведение величин 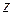 и
и 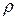 — медленное изменение, приближенно линейное во времени. Так как измерения производятся один раз в единицу дискретного времени
— медленное изменение, приближенно линейное во времени. Так как измерения производятся один раз в единицу дискретного времени 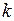 , наши уравнения естественно записать как разностные (дискретные).
, наши уравнения естественно записать как разностные (дискретные).
Эти соображения, в сочетании с естественным стремлением сделать модель максимально простой, приводят к следующим линейным стохастическим уравнениям:
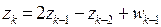 ,
, 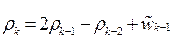 . (4)
. (4)
Здесь индекс 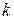 нумерует дискретные моменты времени,
нумерует дискретные моменты времени, 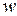 и
и 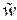 — шумы процесса. В отсутствие этих шумов переменные
— шумы процесса. В отсутствие этих шумов переменные 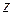 и
и 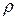 зависели бы от
зависели бы от 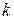 строго линейно. Заметим, что линейное изменение
строго линейно. Заметим, что линейное изменение 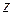 при постоянном
при постоянном 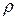 отвечает заполнению или опорожнению емкости с постоянной скоростью, выраженной в единицах массы в единицу времени. Линейное изменение плотности
отвечает заполнению или опорожнению емкости с постоянной скоростью, выраженной в единицах массы в единицу времени. Линейное изменение плотности 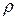 при постоянном
при постоянном 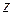 может быть вызвано, например, химической реакцией.
может быть вызвано, например, химической реакцией.
Таким образом, мы относим к «случайным шумам» все факторы, вызывающие отклонения хода изменения величин 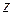 и
и 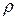 от линейности: дрожание заглушек, открытие/закрытие вентилей человеком или автоматом (информация об этом не передается измерительному устройству) и т.д. Ясно, что характеристики этих шумов могут быть описаны лишь приближенно. Мы будем действовать так, как если бы эти шумы
от линейности: дрожание заглушек, открытие/закрытие вентилей человеком или автоматом (информация об этом не передается измерительному устройству) и т.д. Ясно, что характеристики этих шумов могут быть описаны лишь приближенно. Мы будем действовать так, как если бы эти шумы 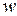 и
и 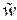 были нормально распределенными случайными величинами с нулевыми математическими ожиданиями и средними квадратичными отклонениями
были нормально распределенными случайными величинами с нулевыми математическими ожиданиями и средними квадратичными отклонениями 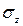 ,
, 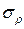 соответственно: практика применения фильтров Калмана показывает, что они успешно работают и во многих случаях отклонения от нормального (гауссова) закона.
соответственно: практика применения фильтров Калмана показывает, что они успешно работают и во многих случаях отклонения от нормального (гауссова) закона.
Уравнения (4) суть два линейных разностных уравнения второго порядка. Стандартная схема фильтра Калмана предполагает, что мы переписываем их в виде одного векторного уравнения первого порядка. Уравнение первого порядка получится из уравнения второго порядка, если мы введем векторы-столбцы, содержащие наряду с величинами 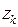 и
и 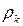 также их значения в предыдущий момент времени, т.е.
также их значения в предыдущий момент времени, т.е. 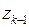 и
и 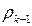 . Получаем уравнение
. Получаем уравнение
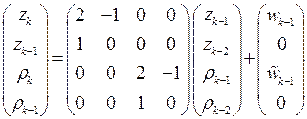 . (5)
. (5)
Удобно ввести следующие обозначения:
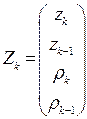 (6)
(6)
мы будем называть 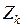 вектором состояния, и
вектором состояния, и
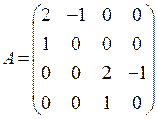
— матрица, описывающая эволюцию этого вектора в отсутствие шумов.
3. Уравнение, описывающее процесс измерения.
Уравнение (5) есть уравнение процесса, и к нему требуется еще добавить уравнение, описывающее измерения. Это будет соотношение (3), записанное через столбец 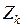 , определенный согласно (6), и с добавленным шумом измерения:
, определенный согласно (6), и с добавленным шумом измерения:
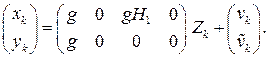 (7)
(7)
Мы введем следующие обозначения:
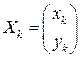 ,
,
причем будем называть 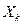 вектором результатов измерения, а также
вектором результатов измерения, а также
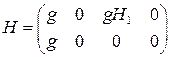
для матрицы, входящей в уравнение (7).