Фильтр Калмана и его применение к задаче.

1. Общие сведения о фильтре Калмана в случае линейной задачи с дискретным временем.

Согласно общей теории фильтра Калмана, алгоритм его работы таков: сначала задаются начальные значения среднего значения вектора состояния 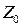и его матрицы ковариаций 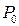. Далее на каждом шаге дискретного времени 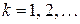выполняются две совокупности операций: прогноз и корректировка.

1.1. Задание начальных значений.

В качестве начального вектора состояния естественно взять вектор

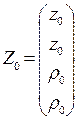, (8)

состоящий из величин, вычисленных согласно формулам (2) по данным датчиков в начальный (нулевой) момент времени, т.е.

, .

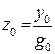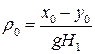Что касается матрицы ковариаций 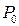, ее наиболее целесообразный выбор обсуждается ниже в пункте 2.

1.2. Прогноз.

Прогнозируем 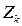по 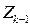, точнее, строим ожидаемые значения его среднего

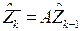(9)

и корреляционной матрицы

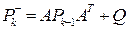. (10)

Знак минус сверху при величинах (9) и (10) подчеркивает, что это лишь предварительные оценки, полученные до измерения реального 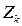. Верхний индекс 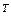означает транспонирование матрицы. Матрица 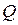есть корреляционная матрица шума процесса, входящего в уравнение (5).

1.3. Корректировка.

Вычисляем матричный «коэффициент Калмана» (Kalman gain):

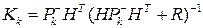, (11)

здесь 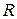— корреляционная матрица шума измерения, входящего в уравнение (7). Формула (11) для матрицы 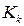получается из требования минимизации следа апостериорной корреляционной матрицы .

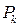Затем обновляем оценку для среднего значения вектора состояния по новым результатам измерения :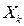

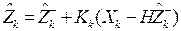, (12)

а также обновляем оценку для корреляционной матрицы:

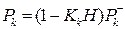. (13)

2. Сходимость матрицы 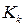к фиксированной матрице для линейных систем и упрощенная схема фильтра Калмана.

Практическая работа с фильтром Калмана в нашем случае линейной стохастической системы и большого количества измерений может быть упрощена. Для этого выделим из пяти уравнений (9)—(13) и рассмотрим отдельно следующие три уравнения: (10), (11) и (13). Они описывают изменение в дискретном времени матрицы ковариаций и коэффициента Калмана. Производимые вычисления независимы не только от оценок средних значений вектора состояния, осуществляемых по формулам (9) и (12), но и вообще от результатов всех текущих измерений (заметим, что в случае нелинейного процесса, для которого применяется обобщенный (extended) фильтр Калмана, это уже было бы не так). Используя численное моделирование (см. следующий раздел), можно увидеть, что после нескольких сотен итераций значения всех элементов матриц, входящих в уравнения (10), (11) и (13), стабилизируются.

Мы будем сразу использовать предельные (заранее вычисленные) выражения для этих матриц. Конкретно, для получения сглаженных оценок вектора состояния требуется одна из них — матрица 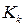. Еще одна — матрица 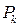— есть оценка матрицы ковариаций этого вектора, нужная для оценки погрешности измерения. Эти выражения могут быть получены исходя из заданных матриц ковариаций шума процесса 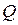и шума измерения 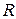с помощью достаточного числа итераций соотношений (10), (11) и (13), см. п. 3.

3. Допущения о характеристиках шума процесса и шума измерения и настройка фильтра.

3.1. Матрица ковариаций шума процесса.

Выбор значений элементов матрицы ковариаций шума процесса 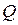осложнен тем, что обычно получение информации об «истинном» ходе процесса затруднено. Оценка же матричных элементов 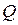может быть осуществлена следующим образом.

Прежде всего, обратимся к уравнению (5). Мы видим, что два элемента вектора шумов (т.е. второго слагаемого в правой части (5)) всегда нулевые — это вызвано тем, что 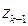и 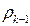в левой части (5) обязаны в точности повторить свои значения, уже находящиеся в правой части (5). Это приводит к тому, что, хотя матрица 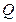имеет размеры 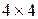, ненулевыми в ней могут быть только 4 элемента, находящиеся на пересечении 1-ой или 3-ей строк с 1-м или 3-м столбцом.

Дальнейшие соображения о величине матричных элементов 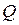могут быть основаны на следующих общих соображениях о ходе технологического процесса. Можно, во-первых, принять, что процессы наполнения—опорожнения, приводящие к изменению массы жидкости (напомним, что величина 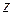пропорциональна массе), идут в среднем независимо от процессов, приводящих к изменению ее плотности. В таком случае величины 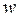и 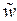в (5) не коррелированы, и внедиагональные элементы матрицы 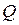равны нулю. Остаются диагональные элементы 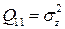и 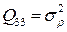, первый из которых отвечает за отклонения хода изменения переменной 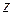от линейности, а второй — аналогично для переменной .

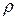Для оценки элемента 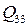можно поступить следующим образом. Рассмотрим 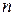уравнений (4) для , :

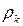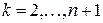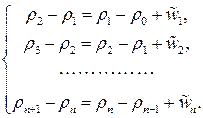
Примем в качестве типичного начального условия, что плотность жидкости в начальный и следующий за ним моменты времени одинаковая: 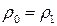. Складывая наши уравнения с учетом этого, получаем:

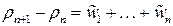. (14)

Рассмотрим случайную величину 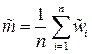. Будучи средним арифметическим большого числа независимых случайных величин, 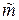является, согласно центральной предельной теореме, нормально распределенной случайной величиной с нулевым математическим ожиданием и дисперсией 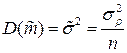, где 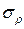— среднее квадратичное отклонение случайной величины .

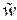С другой стороны, в силу (14) имеем 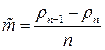. Заметим, что 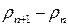есть дискретный аналог скорости изменения плотности 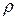. Зная примерный характер изменения 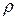в данном технологическом процессе, можно указать интервал, в который с большой вероятностью попадают значения величины 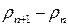, и оценить, следовательно, дисперсию 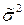величины 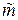и величину 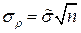. Конкретный пример такой оценки приводится ниже в разделе «Примеры численного моделирования».

Величина дисперсии 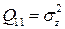шума, относящегося к величине 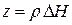, может быть оценена следующим образом. Поскольку наши стохастические уравнения (4) таковы, что шумы представляют дискретные аналоги ускорения соответствующих величин, указанная дисперсия может быть оценена с помощью формулы Лейбница для второй производной произведения, которая приближенно верна и для дискретного времени:

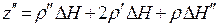. (15)

Предварительно нужно оценить, в частности, характерное ускорение величины 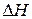. Далее в разделе «Примеры численного моделирования» мы проводим все эти оценки для конкретного примера.

3.2. Матрица ковариаций шума измерения.

Два датчика идентичны по своим характеристикам и работают независимо друг от друга, поэтому матрица ковариаций шума измерения 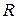запишется в диагональном виде

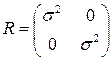. (16)

Здесь среднеквадратичные ошибки 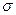для данных датчиков считаем известными.

3.3. Вычисление матрицы ковариаций вектора состояния и матричного коэффициента Калмана.

Как уже отмечалось, матрица 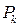ковариаций вектора состояния с ростом 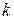быстро стабилизируется и перестает зависеть от своего начального значения 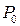. То же происходит и с матричным коэффициента Калмана 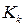. Их предельные значения, однако, зависят от матриц 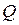и 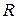и, разумеется, от матрицы 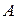, описывающей ход процесса.