Особенности поведения микрочастиц. Принципы описания поведения микрочастиц, волновая функция, соотношение неопределенностей, волна де Бройля. Постулаты Бора. Уравнение Шредингера (временное и стационарное), физический смысл входящих в него членов. Решение стационарного уравнения Шредингера для частицы в одномерном потенциальном ящике и частицы на окружности. Условия появления квантовых явлений. Влияние массы и области локализации частиц. Двумерная потенциальная яма, вырождение квантовых состояний и снятие вырождения. Потенциальная яма конечной глубины и влияние ее глубины и ширины на уровни энергии частицы. Возможность локализации частицы в пространстве. Туннельный эффект. Заполнение уровней и принцип Паули, полная энергия совокупности электронов в квантовой системе. Уровни энергии в атоме водорода, переходы между уровнями. Индивидуальность спектров атомов и эмиссионный спектральный анализ. Металлическая модель молекулы и объяснение корреляции цветности вещества и эффекта сопряжения химических связей в молекулах. Нормальная и инверсная заселенность квантовых состояний. Поглощение, спонтанное и вынужденное излучения. Коэффициенты Эйнштейна. Формула Планка. Усиление света при прохождении через инверсно заселенную среду. Понятие о лазерах.
Физическая природа химической связи. Электронное строение многоэлектронных атомов, гибридизация, объяснение причин появления пространственных форм молекул. Принцип максимального перекрывания. Внутреннее вращение в молекулах и его роль в биохимических реакциях. Движение частиц в многоатомных молекулах и виды молекулярной спектроскопии. Симметрия молекул и появление правил отбора.
Фотохимические реакции и особенности потенциальных поверхностей основных и возбужденных электронных состояний в молекулах. Распад молекул при фотовозбуждениях. Физическая природа фотосинтеза. Транспорт энергии при фотосинтезе. Зонная структура электронных состояний кристаллов. Заполненные и незаполненные зоны. Уровень Ферми. Проводники, полупроводники и диэлектрики. Особенность проводимости в полупроводниках.
Систематика элементарных частиц. Законы взаимопревращений частиц, ядерные реакции, дефект массы. Строение ядер, ядерные силы, устойчивые и неустойчивые ядра, естественная и искусственная радиоактивность. Законы радиоактивного распада. Принципы радиоактивационного анализа. «Меченные» атомы в биологии. Пути использования ядерной энергии.

 Раздел 1. МЕХАНИКА
Раздел 1. МЕХАНИКА
Основные формулы
1. Мгновенная скорость:  =
=  .
.
2. Мгновенное ускорение:  .
.
3. Тангенциальное и нормальное ускорения: 

 .
.
4. Полное ускорение:  .
.
5. Уравнения равнопеременного движения: 
 .
.
6. Второй закон Ньютона:  при m=const,
при m=const,  .
.
7. Работа переменной силы F на пути S:  dS.
dS.
8. Мощность: 
 .
.
9. Кинетическая энергия тела:  .
.
10. Потенциальная энергия: 
11. Закон сохранения механической энергии в консервативных системах:
 .
.
12. Закон сохранения импульса (количества движения) изолированной системы:  где
где 
13. Сила трения скольжения: Fтр=mFn.
14. Сила упругости:  .
.
15. Потенциальная энергия упругого деформированного тела: 
16. Угловая скорость: 
при равномерном вращении:  n.
n.
17. Угловое ускорение: 
18. Соотношение между угловой и линейной скоростями: 
19. Уравнение равнопеременного вращательного движения:


20. Момент инерции материальной точки:  .
.
21. Моменты инерции различных однородных тел относительно оси,
проходящей через центр масс:
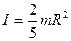 - для шара радиуса R;
- для шара радиуса R;
 - для тонкостенного цилиндра;
- для тонкостенного цилиндра;
 - для сплошного цилиндра, диска (относительно оси,
- для сплошного цилиндра, диска (относительно оси,
совпадающей с геометрической осью цилиндра);
 - для тонкого стержня длины
- для тонкого стержня длины  относительно оси,
относительно оси,
проходящей перпендикулярно стержню через его середину.
22. Момент силы: 
23. Основной закон динамики вращательного движения:
 если
если  =const, то
=const, то 
24. Закон сохранения момента импульса для изолированной системы:

25. Кинетическая энергия вращающегося тела: 
26. Уравнение гармонического колебания: 
27. Циклическая частота:  n.
n.
28. Скорость при гармоническом колебательном движении:

29. Ускорение при гармоническом колебательном движении:

30. Полная энергия при гармоническом колебании:  .
.
31. Уравнение неразрывности струи в установившемся потоке: 
(S - сечение трубки тока,  - скорость потока в сечении S).
- скорость потока в сечении S).
32. Уравнение Бернулли:  g h=const.
g h=const.
Примеры решения задач
Задача 1. Поезд отошел от станции и в течение 20 с двигался равноускоренно. Найдите путь, пройденный поездом за 20 с, если известно, что за десятую секунду он прошел путь 5 м.
Дано:
 0 = 0;
t= 20 c;
S10 – S9= 5 м 0 = 0;
t= 20 c;
S10 – S9= 5 м
 S -?
S -?
|  Решение:
Для определения всего пути S воспользуемся формулой пути, записанной с учетом того, что Решение:
Для определения всего пути S воспользуемся формулой пути, записанной с учетом того, что  0 = 0: 0 = 0: 
 . (1) . (1)
|
Ускорение 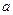 найдем из условия найдем из условия

 . (2)
Подставим (2) в (1) . (2)
Подставим (2) в (1)  .
Подставим численные значения в полученную формулу .
Подставим численные значения в полученную формулу
 .
Ответ: S = 105 м. .
Ответ: S = 105 м.
|
 Задача 2. С какой высоты упало тело, если последнюю четверть пути оно прошло за 0,5 с?
Задача 2. С какой высоты упало тело, если последнюю четверть пути оно прошло за 0,5 с?
Дано:
h2 = ¼ h;
 t2 = 0,5 c.
h -? t2 = 0,5 c.
h -?
| Решение:
Всю высоту найдем из уравнения: 
 , (1)
где t – все время падения , (1)
где t – все время падения
|
 - тело будет падать за t – t2. - тело будет падать за t – t2.
 . (2)
Выразив из (2) высоту и приравняв (1), получим . (2)
Выразив из (2) высоту и приравняв (1), получим 
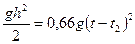 . (3)
Решая уравнение (3), найдем все время падения
t2 = 1,33 (t – 0,5)2; t2 = 1,33 (t – 2t ·0,5 + 0,52);
t2 = 1,33 t2 – 1,33 t + 0,33; 0,33 t2 – 1,33 t + 0,33 = 0. . (3)
Решая уравнение (3), найдем все время падения
t2 = 1,33 (t – 0,5)2; t2 = 1,33 (t – 2t ·0,5 + 0,52);
t2 = 1,33 t2 – 1,33 t + 0,33; 0,33 t2 – 1,33 t + 0,33 = 0.
 ; t1 = 3,78 c; t2 = 0,25 c.
Корень t2 = 0,25 c не соответствует условию задачи, поэтому все время падения будет равно 3,78 с. Подставив данное значение в уравнение (1), получим ; t1 = 3,78 c; t2 = 0,25 c.
Корень t2 = 0,25 c не соответствует условию задачи, поэтому все время падения будет равно 3,78 с. Подставив данное значение в уравнение (1), получим  .
Ответ: 70 м. .
Ответ: 70 м.
|
Задача 3. С вертолета, летящего горизонтально на высоте 125 м со скоростью 25 м/с, бросили груз. На какой высоте скорость груза будет направлена под углом 60о к горизонту?
Дано:
h = 125 м;
 o = 25 м/с; o = 25 м/с;
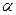 = 60о. = 60о.
 h2 -?
h2 -?
|  Решение: Решение:
  o 0 o 0
        X
h1 X
h1
        F F
Y Рис. 1 | |||||||
Уравнение движения груза в проекциях на оси X и Y имеют вид:
 . (1)
Из рисунка видно, что . (1)
Из рисунка видно, что  y = y =  otg otg 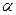 =gt1; =gt1;
 x = x =  0. (2)
Решая (2), получим 0. (2)
Решая (2), получим   .
Подставим (2) в (1) .
Подставим (2) в (1)  ;
h1 = ;
h1 =  ;
h2 = h – h1;
h2 = 125-95,6 = 29,4 м.
Ответ: h2 = 29,4 м. ;
h2 = h – h1;
h2 = 125-95,6 = 29,4 м.
Ответ: h2 = 29,4 м.
|
Задача 4. Из орудия, ствол которого наклонен под углом 600 к горизонту, вылетает снаряд со скоростью 400 м/с. Определить скорость снаряда и его высоту через 4 с после выстрела.
 Дано: Дано:
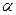 = 600; = 600;
 o = 400 м/с;
t = 4 c. o = 400 м/с;
t = 4 c.
| Решение:
 у у
   у у 

 А А  x x
   0y 0y  0 H 0 H
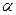
  0x x
Рис. 2 0x x
Рис. 2
| |||
Через 4 с снаряд еще не поднимется до высшей точки, это случится позже, через время  , когда , когда  станет равна нулю. Следовательно, через 4 с тело окажется в точке А. Скорость в точке А станет равна нулю. Следовательно, через 4 с тело окажется в точке А. Скорость в точке А  ,
где ,
где  ; ; 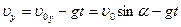 . .

 ; ; 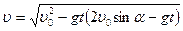 .
Подставим численные значения в полученное уравнение: .
Подставим численные значения в полученное уравнение:
 .
Высоту найдем из уравнения: .
Высоту найдем из уравнения:
 ; ;  .
Ответ: .
Ответ:  = 380 м/с; h = 1312 м. = 380 м/с; h = 1312 м.
|
Задача 5. Зависимость пройденного телом пути s от времени t дается уравнением  , где
, где  , D =0,01 м/с3 и через какое время t тело будет иметь ускорение 1м/с2? Найти среднее ускорение
, D =0,01 м/с3 и через какое время t тело будет иметь ускорение 1м/с2? Найти среднее ускорение 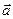 тела за этот промежуток времени.
тела за этот промежуток времени.
 Дано: Дано: 


  t-?
t-? 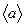 -? -?
| Решение:
Мгновенная скорость 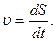 Ускорение Ускорение 
  Таким образом
Таким образом  , откуда , откуда   . Среднее ускорение . Среднее ускорение  . Поскольку . Поскольку
|
 , то можно найти , то можно найти  ; ;  , где , где  ; ; 
  отсюда отсюда    . 0,14 +3. 0,01. 12 м/с2 =0,64 м/с2.
Ответ: . 0,14 +3. 0,01. 12 м/с2 =0,64 м/с2.
Ответ:  ; ;  . .
|
Задача 6. Камень брошен горизонтально со скоростью 10 м/с. Найти радиус кривизны траектории камня через время 3 c после начала движения.
 Дано: Дано:
 x = 10 м/с;
t = 3с. x = 10 м/с;
t = 3с.
 R-?
R-?
|   Решение: Решение:
Рис. 3
| ||||||||||||||||||
Нормальное ускорение камня
 . (1)
Из рисунка видно, что . (1)
Из рисунка видно, что
 . (2)
Из уравнения (1) . (2)
Из уравнения (1) 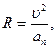 (3)
где (3)
где  ; (4)
sin ; (4)
sin 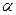 = =  ; (5) ; (5)
 (6)
Сделав соответствующие подстановки в (3), получим: (6)
Сделав соответствующие подстановки в (3), получим: 
 Ответ:
Ответ:  м. м.
|
Задача 7. Точка движется по окружности радиусом 2см. Зависимость пути от времени дается уравнением  где
где  Найти нормальное и тангенциальное ускорения точки в момент, когда линейная скорость точки 0,3 м/с.
Найти нормальное и тангенциальное ускорения точки в момент, когда линейная скорость точки 0,3 м/с.
Дано:





 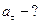
|  Решение:
Нормальная составляющая ускорения: Решение:
Нормальная составляющая ускорения:
 (1)
Тангенциальная составляющая ускорения: (1)
Тангенциальная составляющая ускорения:
 (2) (2)
 . (3) . (3)
|
Из уравнения (3) выразим t =  и подставим в (2) и подставим в (2)
 = 6ct = 6c = 6ct = 6c  ; ;  ; ;
 .
Ответ: .
Ответ:  
|






|

|





 Задача 8. Две гири с массами 2 кг и 1 кг соединены нитью, перекинутой через блок массой 1 кг. Найти ускорение, с которым движутся гири, и силы натяжения
Задача 8. Две гири с массами 2 кг и 1 кг соединены нитью, перекинутой через блок массой 1 кг. Найти ускорение, с которым движутся гири, и силы натяжения  и
и 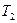 нитей, к которым подвешены гири. Блок считать однородным диском. Трением пренебречь.
нитей, к которым подвешены гири. Блок считать однородным диском. Трением пренебречь.
Рис. 4
Дано:


 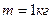
  -? -? 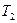 -? -?
|  Решение:
Запишем в векторной форме уравнения поступательного движения первой и второй гири: Решение:
Запишем в векторной форме уравнения поступательного движения первой и второй гири:   и уравнение вращательного движения диска и уравнение вращательного движения диска  где где  - момент силы натяжения нити - момент силы натяжения нити   - момент силы натяжения нити - момент силы натяжения нити 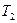 . Спроектируем первые два уравнения на ось y, . Спроектируем первые два уравнения на ось y,
|
а последнее на ось x и добавим уравнение кинематической связи. Получим систему 4 уравнений:
 ; (1) ; (1)
 ; (2) ; (2)
 (3) (3)
 . (4)
Подставим (4) в (3): . (4)
Подставим (4) в (3):
 (5)
Вычтем (2) из (1), подставим в полученное выражение (5) и найдем (5)
Вычтем (2) из (1), подставим в полученное выражение (5) и найдем
 . (6)
Подставляя (6) в (1) и (2), получим . (6)
Подставляя (6) в (1) и (2), получим  
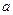 = =   = 2,8 м/с2;
Т1 = 2 (9,8 – 2,8) Н = 14 Н;
Т2 = 1 (9,8 + 2,8) Н = 12,6 Н.
Ответ: = 2,8 м/с2;
Т1 = 2 (9,8 – 2,8) Н = 14 Н;
Т2 = 1 (9,8 + 2,8) Н = 12,6 Н.
Ответ: 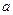 = 2,8 м/с2, Т1 = 14 Н, Т2 = 12,6 Н. = 2,8 м/с2, Т1 = 14 Н, Т2 = 12,6 Н.
|
Задача 9. Горизонтальная платформа массой  вращается вокруг вертикальной оси, проходящей через центр платформы с частотой
вращается вокруг вертикальной оси, проходящей через центр платформы с частотой  Человек массой
Человек массой  стоит при этом на краю платформы. С какой частотой
стоит при этом на краю платформы. С какой частотой  начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека - точечной массой.
начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека - точечной массой.
 |
Дано:
 ; ;
 = =  об/с; об/с;
   .
n2 -? .
n2 -?
|  Решение: Решение:
  Система «человек – платформа» замкнута в проекции на ось Система «человек – платформа» замкнута в проекции на ось  , т.к. моменты сил , т.к. моменты сил  и и  в проекции на эту ось. Следовательно, в проекции на эту ось. Следовательно,
Рис. 5 | ||||||
можно воспользоваться законом сохранения момента импульса.
В проекции на ось  : :
 (1)
где (1)
где  - момент инерции платформы с человеком, стоящим на ее краю, - момент инерции платформы с человеком, стоящим на ее краю,  - момент инерции платформы с человеком, стоящим в центре, - момент инерции платформы с человеком, стоящим в центре,  и и  - угловые скорости платформы в обоих случаях. Здесь - угловые скорости платформы в обоих случаях. Здесь 
 , (2)
где , (2)
где  - радиус платформы. Подставляя (2) в (1) и учитывая, что - радиус платформы. Подставляя (2) в (1) и учитывая, что  , где , где  - частота вращения платформы, получим - частота вращения платформы, получим  ; ;  n2= 0,16 .
n2= 0,16 .  = 0,352 об/с.
Ответ: n2= 0,352 об/с. = 0,352 об/с.
Ответ: n2= 0,352 об/с.
|
 Задача 10. Граната, летевшая горизонтально со скоростью 12 м/с, разорвалась на две части. Массы кусков равны 10 кг и 5 кг. Скорость большого осколка 25 м/с и направлена под углом 300 к горизонту вниз и вперед. Найти величину и направление скорости меньшего осколка.
Задача 10. Граната, летевшая горизонтально со скоростью 12 м/с, разорвалась на две части. Массы кусков равны 10 кг и 5 кг. Скорость большого осколка 25 м/с и направлена под углом 300 к горизонту вниз и вперед. Найти величину и направление скорости меньшего осколка.
Дано:
 = 12 м/с;
m1 = 10 кг;
m2 = 5 кг; = 12 м/с;
m1 = 10 кг;
m2 = 5 кг;
 1 = 25 м/с; 1 = 25 м/с;
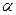 = 300. = 300.
  2 -? 2 -?  -? -?
|  Решение:
у Решение:
у
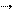   m2 m2  2 2
   m m 
     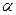 х х
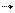 m1 m1  1
Рис. 6 1
Рис. 6
|
Запишем закон сохранения импульса
  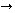 m m  = m1 = m1  1 + m2 1 + m2  2. (1)
В проекциях на оси х и у:
ось х: 2. (1)
В проекциях на оси х и у:
ось х:  ; (2)
ось у: ; (2)
ось у:  . (3)
Решая (2) и (3), получим: . (3)
Решая (2) и (3), получим:  ; ;  . .
 ; ; 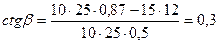 . .
 = 740. = 740.
 ; ;  .
Ответ: .
Ответ:  2 = 26 м/с, 2 = 26 м/с,  = 740. = 740.
|
Задача 11. В небольшой шар массой М, подвешенный на невесомой нерастяжимой нити длиной l, попадает пуля массой m, летящая со скоростью V0 под углом α к горизонту и застревает в шаре. Определить, на какой максимальный угол отклонится нить с шаром от вертикали?
 Дано:
М; m; Дано:
М; m;
 ; ;  0;
α. 0;
α.
 β -?
β -?
|      Решение: Решение:
 
Рис. 7
| ||||||||||||
Запишем закон сохранения импульса тела:
m  = (m + M) = (m + M)  ;
в проекции на ось X:
m ;
в проекции на ось X:
m  0cosα = (m + M) 0cosα = (m + M)  , (1)
где , (1)
где  - скорость шара вместе с пулей.
Найдем из закона сохранения энергии - скорость шара вместе с пулей.
Найдем из закона сохранения энергии
 . (2)
Из рисунка . (2)
Из рисунка  = cos = cos 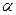 , тогда , тогда
 . (3)
Решая (1), (2), (3) получим . (3)
Решая (1), (2), (3) получим
 .
Ответ: .
Ответ:  . .
|
Задача 12. Материальная точка массой 20 г совершает гармонические колебания с периодом 9 с. Начальная фаза колебаний 10°. Через сколько времени от начала движения смещение точки достигнет половины амплитуды? Найти амплитуду, максимальные скорость и ускорение точки, если полная энергия ее равна 0,001 Дж.
 Дано: Дано:





 



| Решение:
Уравнение гармонического колебательного движения:
 , (1)
где: , (1)
где:  - смещение точки относительно положения равновесия; - смещение точки относительно положения равновесия;
 - амплитуда колебания; - амплитуда колебания;
 - циклическая частота; - циклическая частота;
 - период колебания; - период колебания;
 - время колебания; - время колебания;
 - начальная фаза колебания. - начальная фаза колебания.
| |
Из уравнения (1) можно определить время колебания  : :
 ; ;  ; ;  ; ;
 (2)
Подставляя числовые значения в формулу (2), получим: (2)
Подставляя числовые значения в формулу (2), получим:
 Амплитуду колебания можно определить из формулы полной энергии колеблющейся точки
Амплитуду колебания можно определить из формулы полной энергии колеблющейся точки  : :
 ; (3) ; (3)
 . (4)
Подставляя в формулу (4) числовые значения в единицах СИ, получим: . (4)
Подставляя в формулу (4) числовые значения в единицах СИ, получим:  м = 1,43 м.
Зная амплитуду, можно вычислить максимальную скорость точки, которая определится как первая производная от смещения м = 1,43 м.
Зная амплитуду, можно вычислить максимальную скорость точки, которая определится как первая производная от смещения  по времени: по времени:  Полагая
Полагая  , получаем значение максимальной скорости: , получаем значение максимальной скорости:
 . (5)
Определяем числовое значение: . (5)
Определяем числовое значение:
 Ускорение точки определяется как первая производная от скорости по времени, т.е.
Ускорение точки определяется как первая производная от скорости по времени, т.е.
 . (6)
Считаем при максимальном ускорении . (6)
Считаем при максимальном ускорении  что дает: что дает:  Подставляя все числовые значения в единицах СИ, получаем:
Подставляя все числовые значения в единицах СИ, получаем:  Ответ:
Ответ: 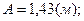  
| ||
Задача 13. Ареометр массы 55 г, плавающий в растворе серной кислоты, указывает, что плотность жидкости 1,27 г/см3. Если прибор сместить из положения его равновесия немного по вертикали и отпустить, он начнет колебаться. Считая колебания незатухающими, определить период колебаний. Радиус трубки ареометра, в которой заключена его шкала, равен 0,30 см.
 Дано: Дано:

 T-? T-?
| Решение:
На погруженный в жидкость ареометр действуют две силы: сила тяжести  и выталкивающая, архимедова сила и выталкивающая, архимедова сила  , равная весу жидкости, вытесненной телом: , равная весу жидкости, вытесненной телом:
 (1) (1)
| ||
где  - объем вытесненной жидкости, равный объему погруженной части ареометра. Выясним соотношение между действующими на тело силами в двух случаях:
1) ареометр находится в равновесии. Приложенные к нему силы уравновешиваются. Приняв направление вниз за положительное, запишем - объем вытесненной жидкости, равный объему погруженной части ареометра. Выясним соотношение между действующими на тело силами в двух случаях:
1) ареометр находится в равновесии. Приложенные к нему силы уравновешиваются. Приняв направление вниз за положительное, запишем
 (2)
2) ареометр смещен из положения равновесия по вертикали на величину (2)
2) ареометр смещен из положения равновесия по вертикали на величину  ( ( алгебраическая величина). Поскольку изменится объем погруженной части прибора, выталкивающая сила также изменится. К ареометру будет приложена равнодействующая, направленная по вертикали и равная алгебраическая величина). Поскольку изменится объем погруженной части прибора, выталкивающая сила также изменится. К ареометру будет приложена равнодействующая, направленная по вертикали и равная
 (3)
где (3)
где  изменение объема погруженной части прибора. Подставив в (4) это значение изменение объема погруженной части прибора. Подставив в (4) это значение  и раскрыв скобки, получим с учетом (1) и раскрыв скобки, получим с учетом (1)
 (4)
где (4)
где  постоянная величина. Видим, что на ареометр действует сила, пропорциональная смещению, взятому с обратным знаком, т.е. квазиупругая сила. Следовательно, он совершает гармонические колебания, период которых найдем по: постоянная величина. Видим, что на ареометр действует сила, пропорциональная смещению, взятому с обратным знаком, т.е. квазиупругая сила. Следовательно, он совершает гармонические колебания, период которых найдем по:   = =
Поиск по сайту©2015-2026 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2016-04-02 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |













 β
β 



 α
α
 х
х