ЗАДАНИЕ 3. Тема: «ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ.

СИМПЛЕКСНЫЙ МЕТОД».

Задача 3.1.

Предприятие планирует выпускать n видов продукции П_i (i= 1, 2, …, n). При её изготовлении используются ресурсы Р₁, Р₂, и Р₃. прямые затраты ресурсов ограничены соответственно величинами b₁, b₂, и b₃. Расход j-го ресурса (j= 1, 2, 3) на единицу продукции i-го вида составляет a_ij ед. Цена единицы продукции i-го вида равна С_i денежных единиц.

Требуется:

1) Составить математическую модель прямой и двойственной задачи. Раскрыть экономический смысл всех переменных, принятых в задаче;

2) Симплексным методом рассчитать план выпуска продукции по видам с учетом имеющихся ограничении ресурсов, который обеспечивал бы предприятию максимальный доход;

3) Используя решение исходной задачи и соответствия между прямыми и двойственными переменными, найти параметры оптимального плана двойственной задачи;

4) Указать наиболее дефицитный и недефицитный (избыточный) ресурс, если он имеется;

5) С помощью двойственных оценок y_j обосновать эффективность оптимального плана, сопоставить оценку израсходованных ресурсов и максимальный доход. Z_max от реализации готовой продукции по всему оптимальному плану и по каждому виду продукции отдельно;

6) Оценить целесообразность приобретения Dbk единиц ресурса K по цене C_k.

Необходимые исходные числовые данные приведены в табл. 3.1.

Табл.3.1

 

Параметр	Номер варианта
а11
а12
а13
а21
а22
а23
а31					5
а32
а33
b1
b2
b3
С1
С2
С3
K
Dbk
Сk

 

Задача 3.2.

 

Составить диету включающие белки, жиры и углеводы в количестве не менее b_i (i = 1, 2, 3). Для составления смеси можно использовать три вида продуктов B_j (j = 1, 2, 3), содержащую белки жиры и углеводы в количестве a_ij. Цена продуктов C_j. Необходимо определить такой набор продуктов, который обеспечил бы необходимое содержание питательных веществ, и полная стоимость его при этом была бы наименьшей.

 

Требуется:

1) Составить математическую модель прямой и двойственной задач. Раскрыть экономический смысл всех переменных, принятых в задаче;

2) Симплекс – методом решить двойственную задачу;

 

Необходимые исходные числовые данные приведена в табл. 3.2.

 

 

Таблица 3.2.

Параметр	Номер варианта
b1
b2
b3
а11
а12
а13
а21
а22
а23
а31
а32
а33
С1
С2
С3

 

ЗАДАНИЕ 4. Тема: «ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ.

ТРАНСПОРТНАЯ ЗАДАЧА».

Задача 4.1

 

В пунктах А_i (i=1, 2, 3)производится однородная продукция в количестве а_i единиц. Себестоимость единицы продукции в i-м пункте равна C_i. Готовая продукция поставляется в пункты В_j (j=1, 2, 3, 4), потребности которых составляют b_j ед. стоимость перевозки единицы продукции из пункта A_i в пункт B_j задана матрицей C_ij.

 

Требуется:

1) Написать математическую модель прямой и двойственной задач с указанием экономического смысла всех переменных;

2) Составить план перевозки продукции, при котором минимизируются суммарные затраты по ее изготовлению и доставке потребителям для условия что продукция произведенная в пункте A_i, где себестоимость её производства наименьшая, распределяется полностью;

3) Вычислить суммарные минимальные затраты Z_min;

4) Узнать в какие пункты развозится продукция от поставщиков;

5) Установить пункты, в которых останется нераспределенная продукция, и указать её объем.

Необходимые исходные числовые данные приведены в таблице 4.1.

Таблица 4.1.

Параметр	Номер варианта
а1
а2
а3
С1
С2
С3
b1					296
b2
b3
b4
С11
С12
С13
С14
С21
С22
С23
С24
С31
С32
С33
С34

Задача 4.2.

 

Трудовые бригады Б₁, Б₂, Б₃ численностью, а₁, а₂, и а₃ человек, сформированы для уборки картофеля.

Для уборки картофеля на четырех полях П₁, П₂, П₃ и П₄ необходимо выделить b₁, b₂, b₃, и b₄ работников. Производительность труда работника зависит от урожайности картофеля, а так же от численности бригады и характеризуется для указанных бригад и полей элементами матрицы P_ij (в центнерах на человека за рабочий день).

Требуется:

1) Распределить работников каждой трудовой бригады по полям так, чтобы за рабочий день было убрано максимально возможное количество картофеля;

2) Определить сколько центнеров картофеля будет убрано с четырех полей при оптимальном распределении работников.

 

Необходимые исходные числовые данные приведены в таблице 4.2.

 

Таблица 4.2.

Параметр	Номер варианта
А1
А2
А3
B1
B2
B3
B4					41
Р11
Р12
Р13
Р14
Р21
Р22
Р23
Р24
Р31
Р32
Р33
Р34

Методические указания

Рассмотрим задачу:

Фирма должна отправить некоторое количество кроватей с трех

складов в пять магазинов. На складах имеется соответственно 15, 25, 20 кроватей. Магазинам необходимо 20, 12, 5, 8 и 12 кроватей. Стоимость перевозки приведена в таблице:

 

Запасы a	Потребности b

 

Стандартную транспортную задачу можно записать следующим

образом:

В рассматриваемом случае количество товара у поставщиков больше, чем полное количество товара, необходимое потребителям. В таком случае при решении задачи приходится вводить фиктивного потребителя. Если потребителям требуется больше товара, чем имеется у поставщиков, ' то следует ввести фиктивного поставщика.

Введем дополнительного потребителя, ему припишем потребность, равную избытку товара, т.е. 3. Стоимость перевозки для фиктивного по­требителя определим равной нулю, так как фактической перевозки товара фиктивному потребителю не будет. Задача стала сбалансированной:

ai

 

В рассматриваемой задаче: п = 6 – количество потребителей, m = 3 – количество поставщиков, a_i – запасы поставщиков, b_j – потребности по­требителей. Искомые переменные определены с двумя индексами для удоб­ства представления решения, значение в (i,j)-й клетке х_ij - объем перевозки от i-го поставщика к j-му потребителю. В стандартной задаче предполага­ется, что суммарный запас товара равен суммарной потребности. При этом предположении одно ограничение является следствием всех дру­гих, поэтому число независимых условий в задаче равно: г = n + m –1.

Приведем математическую модель рассматриваемой задачи:

 

MIN(x₁₁ + 3x₁₃ + 4x₁₄ + 2x₁₅ + 5x₂₁ + x₂₂ + 2x₂₃ + 3x₂₄ + 3x₂₅ + 4x₃₁ + 8x₃₂ + +x₃₃ + 4x₃₄ + 3x₃₅)

x₁₁ + x₁₂ + x₁₃ + x₁₄ + x₁₅ =15

x₂₁ + x₂₂ + x₂₃ + x₂₄ + x₂₅ =25

x₃₁ + x₃₂ + x₃₃ + x₃₄ + x₃₅ =20

x₁₁ + x₂₁ + x₃₁ =20

x₁₂ + x₂₂ + x₃₂ =12

x₁₃ + x₂₃ + x₃₃ =5

x₁₄ + x₂₄ + x₃₄ =8

x₁₅ + x₂₅ + x₃₅ =12

x₁₆ + x₂₆ + x₃₆ =3

 

Для формулировки двойственной задачи вводим симплекс-
множители:

u_i – условные оценки поставщиков, v_j – условные оценки потребителей:

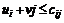, знаки u_i и v_j не определены

Заметим, что в двойственной задаче переменные могут быть как отрицательными, так и положительными. Приведенный ниже алгоритм последовательного улучшения решения задачи (плана) для транспортной задачи является примером ситуации, когда мы предпочитаем решение двойственной задачи решению исходной.

Из второй теоремы двойственности следует, что в клетках, где реше­ние прямой задачи положительно (x_ij>0), ограничения двойственной зада­чи превращаются в равенства (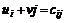), в остальных точках – в строгое неравенство. Это относится к оптимальному решению исходной задачи. Будем строить вычислительный алгоритм так, чтобы на всех итерациях целевые функции прямой и двойственной задачи совпадали:

Для этого будем выбирать u_i и v_j так, чтобы 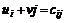для ненулевых x_ij. Этим обеспечивается равенство целевых функций прямой и двойствен­ной задач на каждом шаге. Если для небазисных переменных (x_ij=0) выполняется условие , получено оптимальное решение для обеих задач.

Сформулируем шаги решения транспортной задачи, представив массив транспортных данных в виде таблицы.

Шаг 1. Начальное приближение строится по принципу "по самому дешевому пути перевозится максимально возможное количество груза".

Начинаем построение с выбора начальной клетки, в которой указано минимальное расстояние. Если таких клеток несколько, выбираем любую из них и ставим максимально возможный объем перевозки. В результате этого мы либо забрали весь груз у поставщика, либо удовлетворили запросы потребителя. Рассматриваем теперь поставщика, если у него не выбран весь груз, или потребителя, если его потребности не удовлетворены. Распределяем этот груз, вновь пользуясь общим прави­лом. Повторяем процедуру, до тех пор, пока весь груз не будет распределен. Проверяем, чтобы число "занятых" клеток было равно г.

Если оно меньше г, то в пустую клетку ставим перевозку, равную нулю, и в дальнейшем эту клетку будем считать "занятой".

Начинаем составление плана перевозок для рассматриваемой задачи с клетки (1, 2), в которой указана минимальная стоимость перевозки, т.е. с перевозок реальным потребителям. В эту клетку ставим наибольшую из возможных перевозок, т.е. 12. Мы удовлетворили потребности второго потребителя, но у первого поставщика осталось еще 3 ед. груза, необходи­мо распределить эти 3 ед. Выберем клетку (1, 1), так как в ней указана минимальная стоимость перевозки. Так, последовательно распределяя груз поставщиков и потребителей, последовательно заполняем клетки начального плана:

 

 

Построенный план содержит 8 "занятых" клеток, как и требовалось.

Шаг 2. Вычисляем симплекс - множители: u_i - для ограничений, соответствующих i-й строке, v_j - j-му столбцу.

Для занятых клеток таблицы , что позволяет найти симплекс - множители. Начать следует с того, что один из множителей принять равным нулю. Удобно ставить нуль в той строке или столбце, где больше всего "занятых" клеток. Далее, используя уже найденные мно­жители в строке или столбце, находим новые множители соответственно в столбцах или строках.

Пусть Uz = 0, тогда мы легко находим четыре значения для парамет­ров V₃–V₆, перемещаясь по второй строке. Используя вновь полученные значения V₃–V₆, находим значения параметров U₁–U₃.

 

							Ui
							–4
							–1
Vj

 

 

Шаг З. Проверяем, является ли построенное решение оптимальным, для чего вычисляем () для незанятых клеток таблицы. Для неба­зисных переменных отрицательное значение этой величины показывает, что эта клетка должна войти в базис, так как ее введение уменьшит базис, для чего следует перейти к шагу 4. Если таких клеток нет, решение является оптимальным.

Шаг 4. Вводим неизвестное значение объема перевозки W в выбран­ную клетку и корректируем соседние значения перевозимого груза в "заня­тых" клетках, чтобы сохранить баланс строк и столбцов. После того как во всех строках и столбцах будут сохранены условия баланса груза, переходим к нахождению W из условия, что в одной из выбранных клеток зна­чение перевозки должно стать равным нулю, а в остальных клетках остать­ся положительным. Таким образом, одна клетка будет введена в базис, другая удалена из него с уменьшением общей целевой функции:

 

							Ui
	3+W	12-W					–4
		W	2-W
	17-W		3+W				–1
Vj							W=2

 

Далее переходим к шагу 2.

Закончим расчет приведенного примера.

							Ui
	5+W	10-W					–1
		2+W			12-W
	15-W				W
Vj			-1				W=10

 

							Ui
							–3
Vj							Z=112

 

Сделать анализ решения.