ЦЕЛОЧИСЛЕННАЯ ЗАДАЧА.
Задача 6.1.
Дана математическая модель целочисленной задачи. Для принятия управленческого решения требуется найти оптимальный целочисленный план и максимальное значение целевой функции.
Решить задачу методом ветвей и границ. Данные необходимые для решения, приведены в табл. 6.1.
Таблица 6.1
| Вариант | Математическая модель задачи | ||
| Целевая функция | Ограничения | Условие неотрица-тельности | |

| 
| x1, x2 ≥ 0 | |

| 
| x1, x2 ≥ 0 | |

| 
| x1, x2 ≥ 0 | |

| 
| x1, x2 ≥ 0 | |
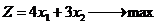
| 
| x1, x2 ≥ 0 | |

| 
| x1, x2 ≥ 0 | |

| 
| x1, x2 ≥ 0 | |

| 
| x1, x2 ≥ 0 | |

| 
| x1, x2 ≥ 0 | |

| 
| x1, x2 ≥ 0 |
ЗАДАЧА ДИСКРЕТНОГО ПРГРАММИРОВАНИЯ.
ЗАДАЧА КОММИВОЯЖЕРА.
Задача 6.2.
Имеется необходимость посетить n городов в ходе деловой поездки. Спланировать поездку нужно так, чтобы, переезжая из города в город, побывать в каждом не более одного раза и вернуться в исходный город. Определить оптимальный маршрут посещения городов и его минимальное расстояние.
Задана матрица расстояний между городами cij. (см.условия задачи).
Сформулированная задача - задача целочисленная. Пусть хij = 1, если путешественник переезжает из i -ого города в j-ый и хij = 0, если это не так.
Формально введем (n+1) город, расположенный там же, где и первый город, т.е. расстояния от (n+1) города до любого другого, отличного от первого, равны расстояниям от первого города. При этом, если из первого города можно лишь выйти, то в (n+1) город можно лишь придти.
Введем дополнительные целые переменные, равные номеру посещения этого города на пути. u1 = 0, un+1 = n. Для того, чтобы избежать замкнутых путей, выйти из первого города и вернуться в (n+1) введем дополнительные ограничения, связывающие переменные xij и переменные ui. (ui целые неотрицательные числа).
2. Математическая модель



Необходимые данные приведены ниже.
Условия задачи 6.2. Матрица расстояний cij
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Вариант 5
Вариант 6
Вариант 7
Вариант 8
Вариант 9
Вариант 10
Вариант 11
Вариант 12
Вариант 13
Вариант 14
Вариант 15
Вариант 16
Вариант 17
Вариант 18
Вариант 19
Вариант 20
Вариант 21
Вариант 22
Вариант 23
Вариант 24
Вариант 25
Вариант 26
Вариант 27
Вариант 28
Вариант 29
Вариант 30
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1. Красс М.С. Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании. –М.: Дело 2000.688с.
2. Кремер Н.Ш. Исследование операций в экономике - М.: Банки и биржи, 1997. - 408 с.
3. Орлов А.И. Теория принятия решений. Учебное пособие. - М.: Издательство "Март", 2004. - 656 с.
4. Федосеев В.В. Экономико-математические методы и прикладные модели. Москва, 2000. – 391 с.
5. Косоруков О.А., Мищенко А.В.. Исследование операций. Учебник для вузов - М.: Изд. Экзамен,2003,-445с.
6. Кундышева Е.С.. Математическое моделирование в экономике. Уч. пособие. –М: Изд «Дашков и К0», 2004,-350с.
7. Экономико – математическое моделирование.Учебник для студентов вузов.Под общ.ред.И.Н.Дрогобыцкого. – изд.»Экзамен»,2004. – 800с. 13. Шапкин А.С, Мазаева Н.П. Математические методы и модели исследования операций:Учебник. – М.:Изд.-торговая корпорация «Дашков и К0»,2004.-400 с.
8. М.С.Красс, Б. П. Чупрынов. Математические методы и модели для магистрантов экономики: Учебное пособие. – СПб.:Питер,2006.-496с.
9.Курицкий Б.Я. Поиск оптимальных решений средствами Excel 7.0. - СПб: BHV, 1997. - 384