Интеграл

сходится при каждом  ,поскольку
,поскольку  ,и интеграл
,и интеграл 
 при
при  сходится.
сходится.
В области  , где
, где  - произвольное положительное число, этот интеграл сходится равномерно, так как
- произвольное положительное число, этот интеграл сходится равномерно, так как  и можно применить признак Вейрштраса. Сходящимся при всех значениях
и можно применить признак Вейрштраса. Сходящимся при всех значениях  является и весь интеграл
является и весь интеграл 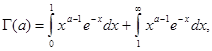 так как и второе слагаемое правой части является интегралом, заведомо сходящимся при любом
так как и второе слагаемое правой части является интегралом, заведомо сходящимся при любом  .Легко видеть что интеграл сходится по
.Легко видеть что интеграл сходится по  в любой области
в любой области  где
где  произвольно. Действительно для всех указанных значений
произвольно. Действительно для всех указанных значений  и для всех
и для всех 
 ,и так как
,и так как 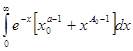 сходится, то выполнены условия признака Вейерштрасса. Таким образом, в области
сходится, то выполнены условия признака Вейерштрасса. Таким образом, в области  интеграл
интеграл  сходится равномерно.
сходится равномерно. 
Отсюда вытекает непрерывность гамма функции при  .Докажем дифференцируемость этой функции при
.Докажем дифференцируемость этой функции при  .Заметим что функция
.Заметим что функция 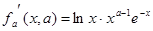 непрерывна при
непрерывна при  и
и  , и покажем,что интеграл:
, и покажем,что интеграл:

сходится равномерно на каждом сегменте  ,
, 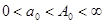 . Выберем число
. Выберем число  так, чтобы
так, чтобы  ; тогда
; тогда  при
при  .Поэтому существует число
.Поэтому существует число  такое, что
такое, что  и
и  на
на  .Но тогда на
.Но тогда на  справедливо неравенство
справедливо неравенство

и так как интеграл  сходится, то интеграл
сходится, то интеграл  сходится равномерно относительно
сходится равномерно относительно 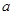 на
на  . Аналогично для
. Аналогично для  существует такое число
существует такое число 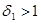 , что для всех
, что для всех  выполняется неравенство
выполняется неравенство 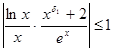 . При таких
. При таких  и всех
и всех  получим
получим  , откуда в силу признака сравнения следует, что интеграл
, откуда в силу признака сравнения следует, что интеграл  сходится равномерно относительно
сходится равномерно относительно 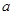 на
на 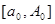 . Наконец, интеграл
. Наконец, интеграл

в котором подынтегральная функция непрерывна в области
 , очевидно, сходится равномерно относительно
, очевидно, сходится равномерно относительно 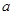 на
на 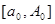 . Таким образом, на
. Таким образом, на  интеграл
интеграл

сходится равномерно, а, следовательно, гамма-функция бесконечно дифференцируема при любом  и справедливо равенство
и справедливо равенство

 .
.
Относительно интеграла  можно повторить те же рассуждения и заключить, что
можно повторить те же рассуждения и заключить, что

По индукции доказывается, что Г-функция бесконечно дифференцируема при  и для ее я
и для ее я  -ой производной справедливо равенство
-ой производной справедливо равенство

Изучим теперь поведение  - функции и построим эскиз ее графика. (см. Приложение 1)
- функции и построим эскиз ее графика. (см. Приложение 1)
Из выражения для второй производной  -функции видно, что
-функции видно, что  для всех
для всех  . Следовательно,
. Следовательно,  возрастает. Поскольку
возрастает. Поскольку  , то по теореме Роля на сегменте [1,2]производная
, то по теореме Роля на сегменте [1,2]производная  при
при 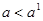 и
и  при
при 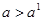 , т. е. Монотонно убывает на
, т. е. Монотонно убывает на  и монотонно возрастает на
и монотонно возрастает на  . Далее, поскольку
. Далее, поскольку  , то
, то 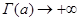 при
при 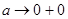 . При
. При  из формулы
из формулы  следует, что
следует, что  при
при  .
.
Равенство  , справедливое при
, справедливое при  , можно использовать при распространении
, можно использовать при распространении  - функции на отрицательное значение
- функции на отрицательное значение 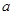 .
.
Положим для  , что
, что  . Правая часть этого равенства определена для
. Правая часть этого равенства определена для 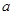 из (-1,0). Получаем, что так продолженная функция
из (-1,0). Получаем, что так продолженная функция  принимает на (-1,0) отрицательные значения и при
принимает на (-1,0) отрицательные значения и при  , а также при
, а также при  функция
функция  .
.
Определив таким образом 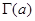 на
на  , мы можем по той же формуле продолжить ее на интервал (-2,-1). На этом интервале продолжением
, мы можем по той же формуле продолжить ее на интервал (-2,-1). На этом интервале продолжением  окажется функция, принимающая положительные значения и такая, что
окажется функция, принимающая положительные значения и такая, что 

 при
при  и
и 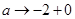 . Продолжая этот процесс, определим функцию
. Продолжая этот процесс, определим функцию  , имеющею разрывы в целочисленных точках
, имеющею разрывы в целочисленных точках 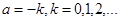 (см. Приложение 1.)
(см. Приложение 1.)
Отметим еще раз, что интеграл

определяет Г-функцию только при положительных значениях 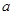 , продолжение на отрицательные значения
, продолжение на отрицательные значения 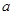 осуществлено нами формально с помощью формулы приведения
осуществлено нами формально с помощью формулы приведения 
 .
.
Вычисление некоторых интегралов.
Формула Стирлинга
Применим гамма функцию к вычислению интеграла:

где m > -1,n > -1.Полагая, что 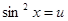 ,имеем
,имеем

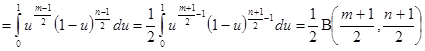
и на основании (2.8) имеем

(4.1)
В интеграле

Где k > -1,n > 0,достаточно положить 
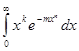

Интеграл

Где s > 0,разложить в ряд



= 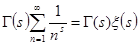
где  дзетта функция Римана
дзетта функция Римана
Рассмотрим неполные гамма функции (функции Прима)

связанные неравенством


Разлагая,  в ряд имеем
в ряд имеем

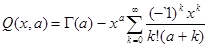
Переходя к выводу формулы Стирлинга, дающей в частности приближенное значение n! при больших значениях n,рассмотрим предварительно вспомогательную функцию
 (4.2)
(4.2)
Непрерывна на интервале (-1,  ) монотонно возрастает от
) монотонно возрастает от  до
до  при изменении
при изменении  от
от  до
до  и обращаются в 0 при u = 0.Так как
и обращаются в 0 при u = 0.Так как

то  при u > 0 и при u < 0, далее имеем
при u > 0 и при u < 0, далее имеем
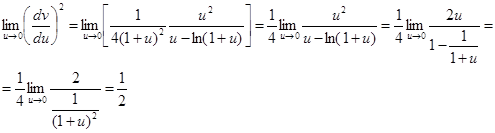
И так производная непрерывна и положительна во всем интервале  ,удовлетворяет условию
,удовлетворяет условию
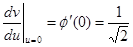
Из предыдущего следует, что существует обратная функция,  определенная на интервале
определенная на интервале  непрерывная и монотонно возрастающая в этом интервале,
непрерывная и монотонно возрастающая в этом интервале,
Обращающаяся в 0 при v=0 и удовлетворяющая условие


(4.3)
Формулу Стирлинга выведем из равенства

полагая  ,имеем
,имеем

Положим далее  введенная выше обратная функция, удовлетворяющая условиям u = -1при
введенная выше обратная функция, удовлетворяющая условиям u = -1при  ,и
,и 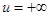 при
при  .Замечая что(см.4.2)
.Замечая что(см.4.2)

имеем
 ,
,
полагая на конец,  ,получим
,получим

или

в пределе при  т.е. при
т.е. при  (см 4.3)
(см 4.3)

откуда вытекает формула Стирлинга

которую можно взять в виде

(4.4)
где  ,при
,при 

для достаточно больших  полагают
полагают

(4.5)
вычисление же производится при помощи логарифмов

если  целое положительное число, то
целое положительное число, то 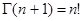 и (4.5) превращается в приближенную формулу вычисления факториалов при больших значениях n
и (4.5) превращается в приближенную формулу вычисления факториалов при больших значениях n

приведем без вывода более точную формулу

где в скобках стоит не сходящийся ряд.