Важным этапом развития теории размещения было открытие немецким ученым Вильгельмом Лаунхардтом (Carl Wilhelm Friedrich Launhardt) метода нахождения пункта оптимального размещения отдельного промышленного предприятия относительно источников сырья и рынка сбыта продукции. Это открытие он описал в статье «Практика эффективного размещения предприятий» («The Determination of the Practical Location of an Industrial Enterprise»), которая была опубликована в 1882 г.
Рассмотренную им задачу принято называть «проблемой 3-х точек».
Пусть требуется найти пункт размещения нового металлургического завода. Известны пункт добычи железной руды - точка A пункт добычи угля - точка В и пункт потребления металла - точка С. Транспортный тариф равен t (на 1 т/км). Расходы руды на выплавку 1т металла составляют: а; расход угля — b. Известны также расстояния между пунктами (стороны локационного треугольника): АС = S 1; ВС = S 2; АВ = S 3.
Возможным пунктом размещения металлургического завода может быть в принципе каждая из трех точек размещения источников руды, угля и потребителя металла. В этих случаях суммарные затраты, связанные с перевозкой всех необходимых грузов для потребления 1т металла, будут равны:
(b S 3 + S 1) t — при размещении завода в точке А;
(a S 3 + S 2) t — при размещении завода в точке В;
(a S 1 + S 2) t — при размещении завода в точке С.
Наилучшим пунктом размещения завода из рассмотренных трех будет тот, в котором транспортные затраты минимальны. Однако искомый пункт размещения может не совпадать ни с одной из вершин локационного треугольника, а находиться внутри него в некоторой точке М.
Расстояние от внутренней точки М до вершин треугольника составляют: AM = r 1 ВМ = r 2 СМ = r 3. Тогда транспортные издержки при размещении металлургического завода в точке М будут равны Т = (ar 1 + br 2 ++ r 3) t. Выполнение требования Т → min дает точку оптимального местоположения предприятия (см. табл. 1.4).
Таблица 1.4
«Локационный треугольник» В. Лаунхардта
А, В – пункты пр-ва сырья; С – потребитель (рынок сбыта); М – точка возможного размещения производственного предприятия. |  ,(1.5)
где а, b – объем поступлений от поставщиков А и В в тоннах (из расчета производства 1 тонны готового изделия);
r 1, r 2, r 3 –расстояния от поставщиков А, В и центра потребления С до предприятия М
р – транспортный тариф.
 , (1.6)
где xi,yi – координаты п-в А, В, С
x, y – искомые координаты предприятия М
|
Особенности модели Лаунхардта:
- в модели не учитываются различия в ценах земельных участков, трудовых и других ресурсов;
- рассматриваются только 2 источника сырья и материалов и 1 рынок сбыта (потребитель);
- решающий фактор размещения – минимум общих транспортных издержек на единицу производимой продукции;
- применимость модели ограничивается случаем линейных функций транспортных издержек, когда транспортные издержки на 1 милю (км) доставки груза строго пропорциональны весу перевозимых товаров.
Задачу можно решить с использованием инструмента «Поиск решения» в Ms Excel.
Как найти поиск решения в Ms Excel 2007:
«Данные» → «Поиск решения»
или
«Параметры Excel» → «Надстройки» → найти вкладку «Поиск решения» и поставить галочку, после этого иконка «Поиск решения» появится в разделе меню «Данные».
Диалоговое окно инструмента «Поиск решения» показано на рис. 1.1 ниже.
Рис. 1.1. Инструмент «Поиск решения»
После ввода всех параметров необходимо нажать на кнопку «Выполнить». Перед этим можно также зайти в подменю «Параметры» инструмента «Поиск решения», нажав на соответствующую кнопку в диалоговом окне инструмента «Поиск решения». В Параметрах можно дополнительно указать желаемое время нахождения результата, предельное число итераций (вариантов перебора возможных значений), метод оптимизации и др.
Как можно видеть из пояснений к рис. 1.1, для решения задачи необходимо:
1. Определить искомые параметры (переменные);
2. Определить целевую функцию (задать ее формулу, в которой так или иначе должны присутствовать и искомые переменные, а также определить значение, к которому должна стремиться целевая функция);
3. Задать ограничения на переменные. Ограничения могут быть заданы в виде уравнений или неравенств. Ограничения позволяют определить область допустимых значений искомых переменных.
В рассматриваемой нами модели Лаунхардта:
1. Искомые параметры – координаты x, y размещения элемента логистической инфраструктуры (склада, сервисного центра) или иного экономического объекта (завод, офисный центр и т.п.);
2. Целевая функция:
,
где
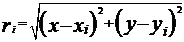- связывает целевую функцию с искомыми параметрами
3. Ограничения определяются, исходя из специфики искомых переменных и условий задачи, и могут быть не заданы вовсе.
Задание для самостоятельного выполнения: Планируется, что завод М будет выпускать в год не менее 10000 ед. продукции X. Для выпуска 1 единицы продукта X потребуется 2 единицы материала А и 4 единицы материала В. Единица материала А весит 30 кг, а единица материала Б – 25 кг. Определить координаты оптимального расположения предприятия М, если известны координаты производителей материалов А, В и оптового склада С. Данные по транспортному тарифу и координатам пунктов А, В и С приведены по вариантам в табл. 1.5.
Примечание: При расчете расстояний принимайте, что они измеряются в километрах.
Таблица 1.5
Исходные данные для решения задачи
| Вариант | Тариф, у.е | А | В | С |
| (2; 10) | (3; 3) | (15; 7) | ||
| (2; 5) | (3; 10) | (7; 7) | ||
| (3; 3) | (8; 12) | (7; 7) | ||
| (5: 7) | (7; 7) | (3; 17) | ||
| (6; 6) | (4; 12) | (5; 15) | ||
| (3; 9) | (2; 6) | (7; 14) | ||
| (4; 4) | (2; 11) | (3; 5) | ||
| (8; 3) | (4; 2) | (5; 11) | ||
| (1; 7) | (5; 4) | (6; 12) | ||
| (2; 9) | (7; 3) | (4; 4) | ||
| (7; 1) | (4; 4) | (6; 3) | ||
| (2; 4) | (3; 3) | (8; 4) |