Помимо координатных методов для выбора мест оптимального расположения складов в регионе обслуживания компании могут быть использованы так называемые «модели выбора». Одним из методов, позволяющих реализовать выбор оптимального места расположения склада является метод относительных предпочтений (МОП).
Суть метода относительных предпочтений состоит в сравнении попарно факторов и возможных вариантов решений по всем, определяющим выбор, факторам. Значимость факторов определяется на основе экспертных оценок или предпочтений выбирающего. Значения факторов рассчитываются, если это возможно, либо определяются в баллах по результатам экспертиз. Окончательное решение в виде вектора весовых коэффициентов вариантов решений находится из матричного уравнения. Наибольший весовой коэффициент соответствует наилучшему варианту решения.
Алгоритм МОП в матричном представлении:
1. Описание задачи
Пусть имеется число j = 1÷m возможных вариантов решения (из которых делается выбор) и число i = 1÷n факторов предпочтения, с учетом значения которых делается выбор в пользу того или иного варианта решения.
Известны также значения значимости каждого фактора - ai и данные оценки варианта решения по каждому из факторов: xij.
Шаг 1: Факторы сравниваются попарно между собой путем деления значения значимости одного на значение значимости другого:
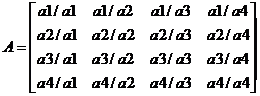 (2.1)
(2.1)
Шаг 2: Находим сумму значений элементов по столбцам матрицы (A):
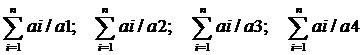 (2.2)
(2.2)
Шаг 3: Составляем промежуточную матрицу A`, которая получается делением каждого значения элемента исходной матрицы A на соответствующую сумму по столбцу (2.2):
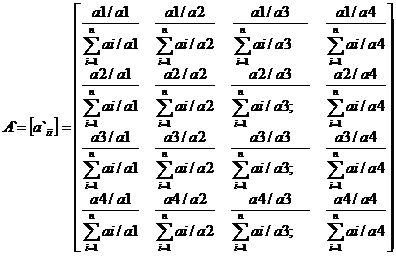 (2.3)
(2.3)
Шаг 4: Находим вектор весовых значений факторов, для чего суммируем по строкам значения элементов матрицы A` и умножаем каждую сумму на 1/n:
 (2.4)
(2.4)
В результате получим весовой вектор факторов:
 (2.5)
(2.5)
Сумма элементов вектора G должна равняться 1!
 (2.6)
(2.6)
Шаг 5: Выполняем обращение значений оценок вариантов решения по факторам, если это необходимо (см. исходные данные):
 (2.7)
(2.7)
Получаем матрицу исходных данных, со значениями которой будем далее работать:
 (2.8)
(2.8)
Шаг 6: Строятся матрицы предпочтений вариантов решения по каждому из n факторов – матрицы Вi.
Значения этих матриц формируются также как и матрицы A, но в качестве элементов будут выступать элементы соответствующей строки матрицы X`. В качестве примера приведем вариант заполнения матрицы B1, которая отражает сравнительное предпочтение вариантов решений по 1-му фактору:
 (2.9)
(2.9)
Шаг 7: Для каждой матрицы Bi находим сумму значений элементов по столбцам (аналогично действию на шаге 2 для матрицы A).
Шаг 8: Составляем промежуточные матрицы Bi`, которые получаются делением каждого значения элемента исходных матриц Bi на соответствующие суммы по столбцам исходных матриц, найденные на шаге 7.
Шаг 9: Аналогично действиям на шаге 4 получаем для каждой матрицы Bi весовой вектор Fi.
Шаг 10: Из весовых векторов Fi. Получаем матрицу F, столбцы которой соответствуют вариантам решения, а строки – фактором сравнения решений.
Шаг 11: Используя формулу умножения матриц в Ms Excel находим вектор итогового решения Vj:
Vj= Fij⋅Gi (2.10)
То есть мы находим произведение весового вектора факторов G, полученного на шаге 4, на матрицу F, полученную на шаге 10.
Наибольшее значение вектора V (R= max (v1, v2,..., vm)) соответствует наилучшему варианту решения.
Процедура умножения матриц:
1. Выделить область под ответ. В данном случае это столбец размером m – по количеству вариантов решений.
2. В выделенной области ввести знак =.
3. Выбрать функцию «Умножение матриц» (МУМНОЖ(__;___)).
4. В диалоговом окне (Рис.1) ввести перемножаемые матрицы: Массив 1 – матрица U Массив 2 – вектор G.
5. После ввода массивов нажать одновременно комбинацию клавиш
Shift+Ctrl+Enter
В выделенную область будет выведен результирующий вектор V.
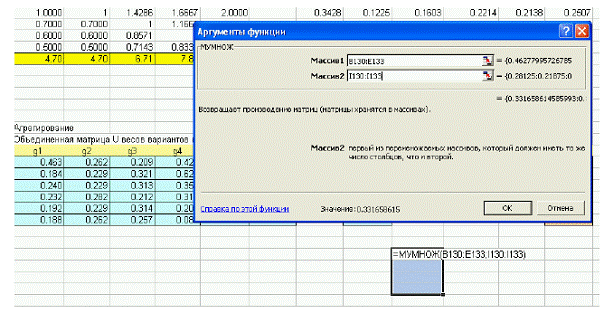
Рис 2.1. Меню оператора умножения матриц в Ms Excel
Задание для самостоятельного решения:
Используя приведенный выше алгоритм средствами Ms Excel решить задачу выбора города в регионе для создания в нем регионального склада товаров. Исходные данные приведены в табл.2.1-2.2. Вариант расчетной формы приведен на рис. 2.2.
Таблица 2.1
Сравнительная значимость факторов
| Фактор | Номер фактора (i) | Значимость фактора (ai) |
| Расстояние транспортировки, тыс. км | ||
| Стоимость аренды склада, у.е./м2 в год | ||
| Объемный спрос на товары, тыс.м3 в год | ||
| Состояние и перспективы развития рынка |
Факторы, требующие обращения: № 1 и №2:

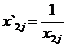
Таблица 2.2
Данные по оценке каждого варианта решения по факторам до обращения (Xij)
| Вариант задания | Множество вариантов размещения склада (j) | |||||||||||||||
| Н.Новогород (j=1) | Самара (j=2) | Казань (j=3) | Саратов (j=4) | |||||||||||||
| Значение экспертной оценки каждого варианта по факторам xij | ||||||||||||||||
| X11 | X21 | X31 | X41 | X12 | X22 | X32 | X42 | X13 | X23 | X33 | X43 | X14 | X24 | X34 | X44 | |
| 3,4 | 3,1 | 2,6 | 3,8 | |||||||||||||
| 3,5 | 3,5 | 2,4 | 2,3 | |||||||||||||
| 3,5 | 2,5 | 2,2 | 2,8 | |||||||||||||
| 3,4 | 3,4 | 3,2 | 2,9 | |||||||||||||
| 2,4 | 3,7 | 3,7 | 3,5 | |||||||||||||
| 2,9 | 2,4 | 2,8 | 2,6 | |||||||||||||
| 2,5 | 3,8 | 3,8 | ||||||||||||||
| 2,5 | 3,7 | 2,9 | 3,5 | |||||||||||||
| 3,5 | 3,5 | 2,5 | 2,9 | |||||||||||||
| 3,7 | 2,5 | 2,3 | ||||||||||||||
| 2,6 | 3,1 | 2,5 | 2,7 | |||||||||||||
| 3,8 | 2,4 | 3,9 |

Рис. 2.2. Образцы расчетных форм при решении задачи выбора месторасположения склада методом относительных предпочтений