Линзой называется шлифованное стекло или любое другое прозрачное вещество, ограниченное с двух сторон сферическими поверхностями; в частном случае одна из поверхностей линзы может быть плоской. Линзы разделяются на два класса: собирающие (выпуклые) и рассеивающие (вогнутые).
Эти определения применимы для линз, имеющих больший коэффициент преломления, чем среда, из которой падают лучи.
Сферические линзы применяются для получения изображений и собирания световых пучков.
Линзы бывают тонкие и толстые. Тонкой называется линза, толщина которой мала по сравнению с радиусами кривизны ограничивающих ее поверхность.
Рассмотрим тонкую собирающую линзу (рис. 1а). На рисунке С – оптический центр – точка, проходя которую лучи не изменяют направления.
а) б)
 |
С 
С
L L
Рис 1
Всякая прямая, проходящая через оптический центр, называется оптической осью, и если она, кроме того, проходит через центры кривизны ( и ) – главной оптической осью. Плоскость, перпендикулярная главной оптической оси и проходящая через оптический центр, называется главной плоскостью линзы.
Главным фокусом линзы называется точка, в которой пересекаются после преломления в линзе лучи, падающие не нее пучком, параллельным главной оптической оси (на рис. 1 точки и 
). Расстояние главного фокуса до оптического центра линзы (расстояние 
и 
) называется главным фокусным расстоянием и является основной характеристикой линзы. Для собирающих линз главное фокусное расстояние – величина положительная, для рассеивающих – отрицательная. Часто линзу характеризуют оптической силой 
величиной, обратной главному фокусному расстоянию и измеряемой в диоптриях (1 дп = 1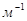 
). Для рассеивающих линз главный фокус является мнимым, и для его отыскания берут не сами лучи, а их продолжение (рис. 1б).
|
|
Для построения изображения предмета с помощью линзы пользуются лучами, ход которых через линзу известен. Обычно берут два луча из следующих трех (рис. 2):
 |
А 2
В 3 
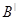
Рис. 2
Луч 1, проходящий через оптический центр (он пройдет через линзу, не преломляясь);
Луч 2, падающий на линзу параллельно ее главной оптической оси (этот луч при выходе из линзы пройдет через ее главный фокус);
Луч 3, проходящий через главный фокус линзы (он из линзы выйдет параллельно ее главной оптической оси).
Изображение предмета АВ в зависимости от того, на каком расстоянии находится предмет, может получиться увеличенным (как на рисунке) или уменьшенным, действительным (как на рисунке) или мнимым. Мнимым изображением предмета называется такое его изображение, которое находится перед линзой по одну сторону с предметом.
Обозначим через 
(рис. 2) расстояние предмета до линзы, а через 
- расстояние от линзы до изображения. Зависимость между , и 
(фокусным расстоянием) дает нам формулу тонкой линзы:
, (1)
где 
- относительный показатель преломления материала, из которого изготовлена линза;
и 
- радиусы кривизны поверхностей линзы.
Линейное увеличение, даваемое тонкой линзой,
, (2)
т.е. линейным увеличением называется отношение размера изображения предмета к соответствующему размеру предмета.
Для определения главного фокусного расстояния линз пользуются оптической скамьей. Оптическая скамья представляет два параллельных металлических стержня на подставках. Скамья имеет по всей длине миллиметровый масштаб. Вдоль скамьи могут перемещаться на ползушках: предмет (освещенное лампой матовое стекло с нарисованной на нем тушью какой-нибудь меткой), линзы и экран. Предмет, линзы и экран нужно установить так, чтобы их середины лежали на одной прямой, параллельной длине оптической скамьи, плоскость экрана была перпендикулярна к длине оптической скамьи, а ось линзы – ей параллельна.
|
|
Определение главного фокусного расстояния выпуклой и вогнутой линз производится несколько различно, поэтому удобнее будет рассмотреть эти случаи отдельно.
Главное фокусное расстояние F собирающей линзы можно определить по формуле:
, (3)
где - расстояние от оптического центра О линзы 
до предмета 
(рис 3),
- расстояние от оптического центра О линзы до резкого изображения этого предмета 
на экране. Однако величины и непосредственно нельзя определить точно в силу того, что в общем случае оптический центр линзы не совпадает с центром симметрии и найти его положение трудно. Можно поступить следующим образом. Из формулы (3) видно, что величины и можно поменять местами, причем эта формула не изменит свой вид. Практически это означает, что если на месте резкого изображения установить сам предмет , то его изображение получится в том месте, где раньше стоял предмет .
A L
F 
E O
A
F
E O
B 
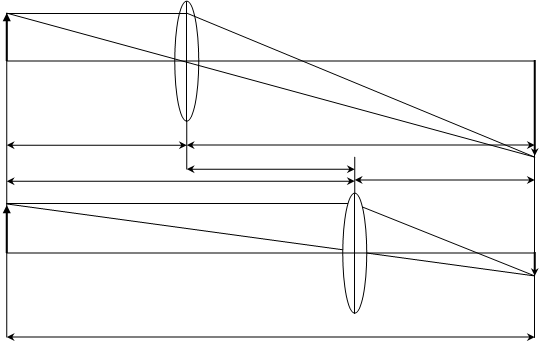
Рис. 3
Последнее, впрочем, можно трактовать еще и так: если, получив, например, резкое обратное и увеличенное изображение предмета на экране, измерить и , а затем, не трогая предмет и экран, передвинуть линзу в положение так, чтобы расстояние между и АЕ равнялось , тогда на экране мы увидим резкое, обратное и уменьшенное изображение , которое будет находиться от как раз на расстоянии (рис. 3). Таким образом, с помощью линзы можно получить два изображения – увеличенное, находящееся на расстоянии от центра линзы, и уменьшенное – на расстоянии , причем величины и связаны между собой формулой (3). Обозначим величину, на которую сместился при этом оптический центр линзы О, через . Эту величину можно измерить перемещением любой точки линзы , так как во время ее перемещения положение оптического центра внутри линзы не изменяется. Последнее обстоятельство позволяет преодолеть указанную выше трудность, заменив измерение перемещения оптического центра линзы О, измерением перемещения какого-нибудь указателя на штативе этой линзы. Из рис. 3 видно, что
|
|
, 
.
Складывая или вычитая эти выражения, получим
, 
.
Подставляя эти выражения и в формулу (3), получим
. (4)
Установка для выполнения этой работы смонтирована на оптической скамье, на которой установлены предмет в виде креста, освещенного лампой накаливания, экран и подвижный штатив с линзой.