1. Вращением окуляра (9) поля зрения и окуляра (10) шкалы сахариметра добиться резкой видимости штрихов и цифр шкалы и нониуса, а также полуокружностей бикварцевой пластинки.
2. Произвести установку сахариметра на нуль. Для этого медленным вращением головки кремальерной передачи (ручка 8), добиться равной освещенности обеих полуокружностей. Проверяем нулевую точку прибора.
3. В камеру (1) поместить трубку с раствором сахара известной концентрации С1 (в трубке не должно быть пузырьков воздуха); при этом равная освещенность поля зрения пропадает.
4. При помощи кремальерной передачи (ручка 8) вновь добиться равной освещенности поля зрения и сделать отсчет (n1) по шкале и нониусу в градусах Вентцке. Пересчитать 
в угловых градусах по формуле:
5. По формуле 
рассчитать удельное вращение.
6. Вновь установить сахариметр на нуль (пункт 2).
7. Теперь в камеру (1) поместить трубку с раствором сахара неизвестной концентрации Сх и аналогичным путем (пункт 4) измерить угол 
поворота плоскости поляризации.
8. По формуле 
рассчитать концентрацию раствора.
9. Повторить опыты (6 – 8) с трубками различной длины (1 дм, 2 дм, 3 дм).
10. Результаты измерений и вычислений занести в таблицу:
| № | 
| 
| 
| С | 
| 
|
    1
| ||||||
        Ср. зн.
|
Контрольные вопросы
1. Какой свет называется естественным, поляризованным?
2. Что такое поляризатор, анализатор?
3. Запишите и поясните закон Малюса.
4. Какие Вы знаете способы получения поляризованного света? Расскажите о них.
5. В чем состоит явление вращения плоскости поляризации?
|
|
6. Как устроен сахариметр?
7. Приведите примеры применения поляризованного света в науке и технике.
Литература
1. И. В. Савельев, Курс общей физики, т. 3
2. Б. М. Яворский, А. А. Детлаф, Курс физики, т. 3
3. Р. И. Грабовский, Курс физики
4. А. С. Шубин, Курс общей физики
ЛАБОРАТОРНАЯ РАБОТА № 12
ПРОВЕРКА ЗАКОНА МАЛЮСА
Цель работы: ознакомление с некоторыми методами получения и исследования линейно поляризованного света.
Задача работы: опытная проверка закона Малюса.
Приборы и принадлежности: поляроиды, источник света, люксметр.
Теоретическое введение
Свет – это поперечная электромагнитная волна, описываемая взаимно перпендикулярными векторами напряженности электрического Е и магнитного Н полей, изменяющимися синхронно (в одинаковой фазе) и перпендикулярными направлению скорости распространения волны. Вектор Е называют еще световым вектором.
Если при распространении световой волны направление колебаний светового вектора бессистемно, хаотически изменяется и, следовательно, любые его направления равновероятны, то такой свет называется естественным.
Е
Е Е
Е Е
Е Е
Е
Рис. 1
Большинство природных и искусственных источников излучают именно такой свет.
Свет, в котором направления колебаний светового вектора упорядочены каким-либо образом, называется поляризованным.
Если колебания вектора Е могут совершаться лишь в одном определенном направлении, то свет называется линейно или плоскополяризованным (рис. 2а).
|
|
Если же колебания вектора Е совершаются так, что его конец описывает круг или эллипс, то свет называется соответственно поляризованным по кругу или эллиптически поляризованным (рис 2 б, в).
Е
Е Е
а) б) в)
Рис 2
Плоскость, в которой колеблется световой вектор (Е), называется плоскостью колебаний. Плоскость, в которой происходит колебание вектора Н, называется плоскостью поляризации. Для получения линейного поляризованного света применяются оптические приборы – поляризаторы.
 |
Луч
Плоскость поляризации – Е
 |
Плоскость колебаний -
Рис. 3
Плоскость колебаний светового вектора в волне, прошедшей через поляризатор, называется плоскостью поляризатора. Поляризатор можно использовать для исследования поляризованного света, т.е. в качестве анализатора. Найдем интенсивность 
линейного поляризованного света после прохождения через анализатор.
Е
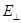
Рис. 4
Пусть Е – амплитуда светового вектора прошедшего поляризатор. 
- плоскость анализатора. Амплитуду Е светового вектора можно разложить на две взаимно перпендикулярные составляющие 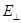и , одна из которых проходит через анализатор. Колебания перпендикулярные к направлению , не проходят через анализатор. Из рис.4 видно, что амплитуда выходящего из анализатора света
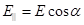
Так как интенсивность света пропорциональна квадрату амплитуды, то
, (1)
где 
- интенсивность поляризованного света, вышедшего из поляризатора; (падающего на анализатор)
- интенсивность поляризованного света, вышедшего из анализатора;
|
|
- угол между плоскостью колебаний падающего на анализатор луча и плоскостью анализатора.
Соотношение (1) носит название закона Малюса.
Поставим на пути естественного луча два поляризатора (второй – анализатор), плоскости которых образуют угол .
Из первого поляризатора выйдет плоскополяризованный луч, интенсивность которого составит половину интенсивности естественного света 
:
.
Согласно закона Малюса из второго поляризатора (анализатора) выйдет свет интенсивности , равной:
Максимальная интенсивность, равная 
, получается при 
(плоскости поляризатора и анализатора параллельны). При 
интенсивность 
(скрещенные поляризатор и анализатор света не пропускают).
Поляризация при двойном лучепреломлении
При прохождении через анизотропные кристаллы световой луч разделяется на два луча. Это явление, получившее название двойного лучепреломления, обнаружил впервые в 1670 г. Бартоломин для исландского шпата (разновидность СаСО3). На рисунке показано прохождение света через кристалл исландского шпата
А В о С
е
Д
Естественный луч АВ, падающий на кристалл, разделяется на два луча ВД и ВС.
Луч ВС называется обыкновенным лучом, т.к. он подчиняется законам преломления, и скорость его в кристалле не зависит от направления.
Луч ВД называется необыкновенным лучом, т.к. показатель преломления его зависит от направления распространения луча, и, следовательно, в различных направлениях в кристалле он распространяется с различными скоростями.
У так называемых одноосных кристаллов имеется направление, вдоль которого не происходит двойное лучепреломление. Это направление называется оптической осью кристалла.
Любая плоскость, проходящая через оптическую ось, называется главным сечением или главной плоскостью кристалла.
Рис. 5
На рисунке 5 сечение МО1NO2 – главное сечение, проходит через оптическую ось и нормаль 
, проведенную через точку В падения луча АВ.
Оба вышедших из кристалла луча полностью поляризованы во взаимно перпендикулярных плоскостях. Плоскость колебаний обыкновенного луча перпендикулярна к главному сечению кристалла. В необыкновенном луче колебания светового вектора совершаются в плоскости, совпадающей с главным сечением. По выходе из кристалла оба луча отличаются друг от друга только направлением поляризации, поэтому названия «обыкновенный» и «необыкновенный» луч имеют смысл только внутри кристалла.
В некоторых кристаллах один из лучей (о или 
) поглощается сильнее другого. Это явление называется дихроизмом. Причина дихроизма – анизотропии поглощения - в анизотропном строении поглощающего вещества. Поэтому следует ожидать, что дихроизмом должны в той или иной степени обладать те поглощающие свет среды, которым свойственно двойное лучепреломление света.
Впервые дихроизм был открыт на монокристаллах минерала турмалина. Одноосный кристалл турмалина обладает двойным преломлением; кроме того, он очень сильно поглощает обыкновенный луч. В нем обыкновенный луч практически полностью поглощается на длине 1 мм. Дихроизм можно использовать на практике для получения линейно поляризованного света из естественного. Однако дихроичные поляризаторы в виде монокристаллических пластинок турмалина не нашли широкого применения из-за их редкости, дороговизны и других недостатков. На практике широко применяются анизотропные пленки, пропитанные анизотропными молекулами или микрокристаллами, например геропатита (сернокислого йод - хинина) – так называемые пленочные поляроиды.
Оптические оси всех кристалликов специальным способом ориентируют в одном направлении. Кристаллы геропатита почти полностью поглощают обыкновенный луч. Таким образом, падающий естественный луч, пройдя сквозь поляроид, становится линейно поляризованным.
В работе используется установка состоящая из источника света S, двух поляроидов 
и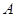 
и люксметра 
. Пройдя сквозь первый поляроид (поляризатор), свет становится плоскополяризованным. Второй поляроид А (анализатор) может пропускать только те колебания, которые совпадают с его главным направлением АА. Если главные направления поляризатора и анализатора совпадают, то интенсивность проходящего света будет максимальной. Если же анализатор повернуть таким образом, что его главное направление составляет угол 
с главным направлением поляризатора, то интенсивность проходящего света будет равна нулю. Такое положение поляроидов называется скрещенным.
П Z
A
S
П A
Рис. 6
В том случае, когда главные направления поляроидов составляют между собой некоторый угол , интенсивность проходящего света будет принимать промежуточные значения.