Задание 1. Определение расстояния между двумя щелями

Задание 1. Определение расстояния между двумя щелями

 

1. Включить лазер.

2. С помощью винтов 3 и 4 установить две щели на оси луча.

3. Получить на экране интерференционную картину от двух щелей, в которой максимумы состоят из группы точек.

4. Измерить расстояние от центрального максимума до любых трех максимумов.

5. Зная расстояние между пластинкой со щелями и экраном (указано на табличке), длину волны (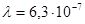 м), определить расстояние между щелями по формуле:

6. Результаты измерений и вычислений занести в таблицу.

 

№ опыта

 

 

Задание 2. Определение ширины щели

1. С помощью винтов 3 и 4 установить щель по оси луча.

2. Получить дифракционную картину, состоящую из чередующихся максимумов и минимумов.

3. Определить расстояние любых трех максимумов от центрального.

4. Зная расстояние между пластинкой со щелями и экраном (указано на табличке), длину волны (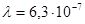 м), определить ширину щели d по формуле:

5. Результаты измерений и вычислений занести в таблицу

 

№ опыта

 

Задание 3. Определение постоянной дифракционной решетки

1. С помощью винтов 3 и 4 установить дифракционную решетку по оси луча.

2. Получить на экране дифракционную картину в виде системы ярких точек.

3. Определить расстояние любых трех максимумов от центрального.

4. Зная расстояние между пластинкой с дифракционной решеткой и экраном (указано на табличке), длину волны (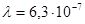 м), определить постоянную дифракционной решетки по формуле:

Для всех заданий рассчитать абсолютную и относительную погрешности.

 

Контрольные вопросы

1. В чем состоит корпускулярно – волновой дуализм свойств света?

2. Что называется интерференцией света?

3. Какие волны называются когерентными?

4. Записать уравнение бегущей электромагнитной волны.

5. Записать условие максимума и минимума для интерференции.

6. Что называется дифракцией света?

7. Сформулируйте принцип Гюйгенса-Френеля.

8. Объяснить метод зон Френеля.

9. Сделать расчет дифракционной картины от двух щелей, от одной щели.

10. Что такое дифракционная решетка? Записать и пояснить формулу дифракционной решетки.

11. Что произойдет, если дифракционную решетку осветить белым светом?

 

Литература

1. Б.М. Яворский, А.А. Детлаф и др. Курс физики, т.3.

2. А.С. Шубин Курс общей физики.

3. И.В. Савельев Курс общей физики, т.3.

4. Р.И. Грабовский Курс физики

 

 

 

ЛАБОРАТОРНАЯ РАБОТА № 11

ОПРЕДЕЛЕНИЕ КОНЦЕНТРАЦИИ РАСТВОРА

САХАРА САХАРИМЕТРОМ

Цель работы: Получение и исследование поляризованного света, ознакомление с явлением оптической активности

 

Задачи работы:

1. Изучение поляризационных приборов (сахариметра);

2. Определение концентрации раствора сахара.

 

Приборы и принадлежности: сахариметр, набор трубок различной длины с раствором сахара.

 

Теоретическое введение

 

С точки зрения электромагнитной теории свет – это поперечная электромагнитная волна. Электромагнитная волна представляет собой периодическое изменение в пространстве и во времени электрического и магнитного полей, распространяющихся во все стороны от той области пространства, где происходят электромагнитные колебания.

Бегущая электромагнитная волна описывается взаимно перпендикулярными векторами напряженности электрического Е и магнитного Н полей, изменяющимися синхронно (т.е. в одинаковой фазе) и перпендикулярными направлению скорости распространения волны.

Рис. 1

Вектор Е называется световым вектором, и все дальнейшие рассуждения мы ограничим рассмотрением этого вектора, так как он играет более важную роль в большинстве известных процессов взаимодействия света с веществом.

Если при распространении световой волны направление колебаний светового вектора бессистемно, хаотически изменяется и, следовательно, любые его направления равновероятны, то такой свет называется естественным.

 

 

Е

Е Е

Е Е

Е Е

Е

Рис. 2

 

Большинство природных и искусственных источников света излучают именно такой свет.

Свет, в котором направления колебаний светового вектора упорядочены каким-либо образом, называется поляризованным.

Если колебания вектора Е могут совершаться лишь в одном определенном направлении, то свет называется линейно или плоско поляризованным. (Рис 3а)

Если же колебания вектора Е совершаются так, что его конец описывает круг или эллипс, то свет называется соответственно поляризованным по кругу или эллиптически поляризованным (рис 3 б, в).

 

Е

Е Е

 

а) б) в)

 

Рис. 3

 

Плоскость, в которой колеблется световой вектор (Е), называется плоскостью колебаний. Плоскость, в которой происходит колебание вектора Н, называется плоскостью поляризации. Эти понятия применимы для линейно поляризованных плоских волн. Для получения линейно поляризованного света применяются оптические приборы-поляризаторы.

Плоскость колебаний светового вектора в волне, прошедший через поляризатор, называется плоскостью поляризатора. Поляризатор можно использовать для исследования поляризованного света, т.е. в качестве анализатора. Найдем интенсивность I линейно поляризованного света после прохождения через анализатор.

 

Е

 

 

 

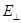
Рис. 4

 

Пусть Е – амплитуда светового вектора, прошедшего поляризатор, - плоскость анализатора. Амплитуду светового вектора Е можно разложить на две взаимно перпендикулярные составляющие 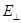и , одна из которых проходит через анализатор. Колебания, перпендикулярные к направлению , не проходят через анализатор. Из рис. 4 видно, что амплитуда выходящего из анализатора света

.

Так как интенсивность света I пропорциональна квадрату амплитуды, то

, (1)

где I₀ – интенсивность поляризованного света, вышедшего из поляризатора (падающего на анализатор);

I_a – интенсивность поляризованного света, вышедшего из анализатора;

- угол между плоскостью колебаний падающего на анализатор луча и плоскостью анализатора.

Соотношение (1) носит название закона Малюса.

Поставим на пути естественного луча два поляризатора (второй – анализатор), плоскости которых образуют угол . Из первого поляризатора выйдет плоскополяризованный луч, интенсивность которого I₀ составит половину интенсивности естественного света I_ест

.

Согласно закона Малюса из второго поляризатора (анализатора) выйдет свет интенсивности I, равной

Максимальная интенсивность, равная , получается при (плоскости поляризатора и анализатора параллельны). При интенсивность I_а=0 (скрещенные поляризатор и анализатор света не пропускают).