Порядок выполнения
1. Расположить на оптической скамье предмет, линзу, осветитель, экран.
2. Перемещая линзу, добиться резкого увеличенного изображения предмета на экране. Фиксируют положение указателя линзы.
3. Передвигая линзу, добиться нового уменьшенного изображения предмета на экране.
4. Измерить расстояние 
между двумя положениями линзы.
5. Измерить расстояние В от предмета до экрана.
6. По формуле 
вычислить главное фокусное расстояние собирающей линзы.
7. По формуле 
рассчитать оптическую силу собирающей линзы.
8. Опыты повторить не менее трех раз.
9. Результаты измерений и вычислений занести в таблицу.
| № опыта | В |
| F | D | 
| 
|
 3
| 
| |||||
  Ср. знач.
|
Задание 2. Определение оптической силы рассеивающей линзы.
Порядок выполнения
Вогнутая или рассеивающая линза дает мнимое изображение. Фокусное расстояние вогнутой линзы определяют следующим образом:
1. Собирают схему, как в первом случае для выпуклой линзы.
2. Замечают точку D (положение экрана, когда получается резкое изображение предмета, рис. 4).
3. Между собирающей линзой L и точкой D помещают рассеивающую линзу 
. Опять добиваются резкого изображения предмета на экране, которое из D перейдет в точку Е. Для линзы «предметом» является изображение в точке D, даваемое линзой L от предмета А. Пользуясь обратимостью хода лучей в системах линз, можно рассматривать эти лучи света как распространяющиеся из точки Е. Тогда точка D будет мнимым изображением точки Е (после преломления лучей в линзе ).
Э Э L
D
E C C
A
Рис. 4
Следовательно, расстояние 
, а 
. Найдем это расстояние (не менее трех раз).
4. Найденные значения и подставляют в формулу (1). Принимая во внимание, что 
и имеют в данном случае отрицательный знак, получим
,
откуда
.
Все полученные опытом и вычислением результаты сводятся в таблицу отсчета.
| № опыта |
|
|
| 
|
    Ср. знач.
|
Задание 3. Определение фокусного расстояния и оптической силы системы 2-х линз.
Порядок выполнения
1. Складывают вместе две тонкие линзы с фокусными расстояниями 
и 
.
2. Повторить пункты 2 – 7 задания №1 и рассчитать оптическую силу системы линз.
3. Проверить полученный результат с результатом теоретическим 
.
Контрольные вопросы
1. Дайте определение линзы. Классификация линз.
2. Дайте определения оптического центра, главной оптической оси, главного фокуса, побочной оси.
3. Покажите построение изображений с помощью различных линз.
4. Запишите и поясните формулу линзы.
5. Дайте определение оптической силы линзы. В каких единицах она измеряется?
6. Чему равна оптическая сила системы линз?
Литература
5. И.В. Савельев Курс общей физики т. 3.
6. Б.М. Яворский, А.А. Детлаф Курс физики, т. 3.
7. А.С. Шубин Курс общей физики.
8. Р.А. Грабовский Курс физики.
ЛАБОРАТОРНАЯ РАБОТА № 9
ОПРЕДЕЛЕНИЕ РАДИУСА КРИВИЗНЫЛИНЗЫ
С ПОМОЩЬЮ КОЛЕЦ НЬЮТОНА
Цель работы: практическое изучение явления интерференции света.
Задачи работы: рассчитать радиус кривизны линзы.
Приборы и принадлежности: установка для получения колец Ньютона, осветитель со светофильтром, миллиметровая линейка.
Краткая теория
Свет с точки зрения классической электродинамики представляет собой поперечные электромагнитные волны, распространяющиеся в вакууме со скоростью 
. Скорость распространения света зависит от оптических свойств среды и определяется формулой:
,
где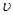 
- скорость света в данной среде;
- абсолютный показатель преломления среды.
В электромагнитной волне колеблются два вектора – напряженности электрического и напряженности магнитного полей:
,
.
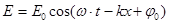Физиологическое, фотохимическое, фотоэлектрическое и другие действия света вызываются колебаниями электрического вектора. Поэтому в дальнейшем мы будем говорить о световом векторе, подразумевая под ним вектор напряженности 
электрического поля.
Пусть две световые волны одинаковой частоты, накладываясь друг на друга, возбуждают в некоторой точке пространства колебания одинакового направления:
Амплитуда результирующего колебания определится формулой:
Если разность фаз складываемых колебаний 
остается постоянной во времени, то волны называются когерентными, а источники таких волн – когерентными источниками.
Если накладываются некогерентные волны, то 
непрерывно изменяется, принимая с равной вероятностью любые значения, вследствие чего среднее во времени значение 
. В этом случае 
, и интенсивность 
результирующей волны равна 
(т.к. 
).
То есть при наложении некогерентных волн происходит сложение интенсивностей, создаваемых каждой из волн в отдельности.
В случае наложения когерентных волн 
имеет для каждой точки пространства свое значение (постоянное во времени), поэтому интенсивность результирующей волны равна:
.
Анализируя это выражение, приходим у выводу, что в тех точках пространства, для которых
;
,
т.е. при наложении когерентных волн происходит перераспределение светового потока а пространстве, в результате чего в одних местах возникают максимумы, а в других минимумы интенсивности света. Это явление называется интерференцией света.
Интерференция света – это пространственное перераспределение энергии светового излучения при наложении когерентных световых волн.
Пусть 2 когерентные волны от двух когерентных источников 
и 
складываются в т. М.
Первая волна до точки М проходит в среде с
показателем 
преломления 
, путь 
. Вторая волна
М проходит в среде с показателем преломления 
путь 
.
Произведение 
называется оптической длиной проходимого волной пути. Величина , равная разности оптических длин проходимых волнами путей, называется оптической разностью хода.
Условия интерференционных максимумов и минимумов имеют вид:
,
,
где 
- порядок интерференционного максимума или минимума (к=0,1,2,3,..).
Т.е., если оптическая разность хода складываемых световых лучей равна четному числу длин полуволн, наблюдается усиление света; если же оптическая разность хода равна нечетному числу полуволн, наблюдается ослабление света.
Интерференцию света можно наблюдать в тонких пленках. Каждому неоднократно приходилось наблюдать радужную окраску мыльных пузырей, тонких пленок масла, бензина, плавающих на поверхности воды, некоторых раковин, покрытых слоем перламутра, крылышек насекомых, перьев птиц, покрытых тонкими, незаметными для глаза, прозрачными чешуйками.
Рассмотрим интерференцию света в тонкой пленке, толщина которой неодинакова в разных местах (Рис. 1).
Падающий на пленку луч 1 разделяется на два луча – отраженный 2 и преломленный 3. Преломленный луч 3 в свою очередь отражается от второй поверхности пленки в т. В и, преломляясь в т. , выходит из пленки (луч 4).
Полученные таким образом два когерентных луча 2 и 4 интерферируют вблизи верхней поверхности пленки в точке С. При малом угле клина и малом угле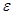 
падения луча точка С будет близка к точке А и практически будет находиться на поверхности слоя. Оптическая разность хода лучей 2 и 4 в этом случае выразится в виде 
(приближенно полагаем AC=DC=0 и AB=BD=d) или
, (1)
где - толщина клина в точке А, - показатель преломления материала клина.
4 2
A C
 |
d
3 
В
Рис. 1
Член 
возникает соответственно «потере» фазы (запаздыванию) на 
при отражении света от оптически более плотного слоя диэлектрика в оптически менее плотный. Знак «+» или «-» берется в зависимости от того, где происходит указанное отражение. Очевидно, в данном случае следует взять знак «-» (отражение от более плотной среды происходит в точке А, следовательно «теряет» фазу первый отраженный луч 2).
Условия интерференционных максимумов и минимумов будут иметь такой вид:
(максимум),
(2)
(минимум),
где к = 0, 1, 2, … - порядок интерференционного максимума и минимума.
Из формул (2) видно, что интерференционные максимумы и минимумы соответствуют определенным толщинам слоя, образуя интерференционные полосы. Поэтому интерференционные полосы в данном случае называются полосами равной толщины.