ПРИМЕРЫРЕШЕНИЯ ЗАДАЧ
П 5. Энергетические эффекты химических процессов.
Термохимические расчеты. Расчет теплоты сгорания топлива.
Пример 1. Термохимическое уравнение реакции. Энтальпии образования вещества.
Напишите термохимическое уравнение реакции, которое отвечает энтальпии образования H2SO4(ж).
Решение. Химические уравнения реакций, в которых указаны агрегатные состояния веществ и тепловые эффекты, называются термохимическими уравнениями.
Стандартной энтальпией (теплотой) образования веществаназывается энтальпия образования 1 моля вещества из простых веществ, если все участники реакции находятся в стандартных состояниях (с.с. при 
и 
моль/л), (Δ fН 0298 см.Приложение 2, [1]
По определению, искомое уравнение должно состоять из исходных простых веществ, устойчивых в стандартном состоянии:
H2(г) + 2O2(г) + S(к) = H2SO4(ж), Δ fН 0298 H2SO4 = −811,3 кДж/моль.
Из табл. (Приложение 2, [1]).
Отрицательное значение энтальпии образования соединения указывает на то, что в результате образования этого соединения из простых веществ теплота выделяется.
Пример 2. Взаимосвязь изменения энтальпии и внутренней энергии в результате реакции.
Рассчитайте изменение внутренней энергии системы при изохорно-изотермическом протекании реакции
С(к) + СО2(г) = 2СО(г)
при с.с. и 298 К.
Решение. Внутренняя энергия системы U – одна из термодинамических функций состояния системы. Изменение внутренней энергии в результате какого-либо процесса (например, химической реакции) Δ rU равно тепловому эффекту этого процесса, протекающего в изохорно-изотермических условиях (QV,T), если при этом не совершается никакой работы:
QV,T = - Δ rU.
Энтальпия Н – одна из термодинамических функций состояния системы.
Изменение энтальпии в результате какого-либо процесса (химической реакции) Δ rН равно тепловому эффекту этого процесса, протекающего в изобарно-изотермических условиях (Qp,T), когда единственным видом работы является работа расширения газа:
Qp,T = - Δ rHТ.
Изменение энтальпии и внутренней энергии в результате реакции связаны соотношением:
Δ rН =Δ rU + ∆ν RT,
где ∆ν – разница между числом молей газообразных продуктов и числом молей газообразных исходных веществ.
Если Δ rН < 0, то процесс идет с выделением тепла в окружающую среду и реакция называется экзотермической; если Δ rН > 0, теплота в результате реакции поглощается и реакция называется эндотермической.
Согласно данным (Приложение 2, [1]):
Вещество Δ fН 0298,кДж/моль
С(графит) 0
СО2 (г) −393,5
СО (г) −110,5
Для расчета энтальпии химической реакции при с.с. и 298 К воспользуемся следствием из закона Гесса:
Δ rН 0298= ∑ν i Δ f Н 0298, продуктов − ∑ν j Δ f Н 0298, исх веществ ;
Δ rН 0298 = 2Δ fН 0298СОг − Δ fН 0298Ск − Δ fН 0298СО2г = 2(−110,5) – 0 – (−393,5) =
= 172,5 кДж. Так как Δ rН 0298 > 0, данная реакция эндотермическая.
Изменение энтальпии и внутренней энергии в результате реакции связаны соотношением:
Δ rН =Δ rU + ∆ν RT.
Тогда ∆ rU 0298 = ∆ rH 0298 – ∆ν RT =
= 172,5 – 1·8,31·298·10−3 = 170,02 кДж. (Разница между числом молей газообразных продуктов и исходных веществ равна ∆ν = 2 − 1 = 1 моль).
Универсальная газовая постоянная R =8,31 Дж/моль.К.
Пример 3. Закон Гесса. Метод циклов.
Вычислите тепловой эффект образования NH3 из простых веществ при стандартном состоянии по тепловым эффектам реакций:
2H2 + O2 = 2H2O(ж);; D r H0 1 = - 571,68 кДж (1)
4 NH3 + 3 O2 = 6 H2O(;ж) + 2 N2 ; D r H0 2 = - 1530,28 кДж (2).
Решение. Закон Гесса: Тепловой эффект реакции зависит от природы и состояния исходных веществ и конечных продуктов, но не зависит от пути реакции, т.е. от числа и характера промежуточных стадий.
Запишем уравнение реакции, тепловой эффект которой необходимо определить:
½N2 + 3/2Н2 = NH3; D r H0 3 = Df H0NH3=?;(3).
В уравнения (1) и (2) входят Н2О (ж) и О2, которые не входят в уравнение (3), поэтому, чтобы исключить их из уравнений (1) и (2), умножим уравнение (1) на 3 и вычтем из него ур (2):
6Н2 + 3О2 – 4NН3 – 3О2 = 6Н2О (ж) – 6Н2О (ж) – 2N2 (г) (4).
После преобразования уравнения (4) и деления его на 4 получаем искомое уравнение (3). Аналогичные действия проделаем с тепловыми эффектами:
(3D rH0 1– D r H02)/4 = D rH0 3. В результате получаем:
D r H0 3 = [3(–571,68) – (– 1530,28)] / 4 = – 46,19 (кДж);
т.е. ∆ f Н0 NH3 = – 46,19 кДж/моль.
Пример 4. Закон Гесса. Метод циклов.
Определите стандартный тепловой эффект реакции:
С(к) + СО2(г) = 2СО(г); (1),
если известны тепловые эффекты двух других реакций:
2С(к) + О2(г) = 2СО(г); ∆ rH 0298 = −221 кДж (2)
и
2СО(г) + О2(г) = 2СО2(г); ∆ rH 0298 = −566,1 кДж (3).
Решение. Закон Гесса: Тепловой эффект реакции зависит от природы и состояния исходных веществ и конечных продуктов, но не зависит от пути реакции, т.е. от числа и характера промежуточных стадий.
Для того, чтобы получить уравнение реакции (1), нужно из уравнения реакции (2) вычесть уравнение реакции (3) и разделить полученное выражение на 2. Те же действия следует проделать и с величинами ∆ rH 0.
Имеем ∆ rH 01 = (∆ rH 02 − ∆ rH 03)/2 = [−221 – (−566,1)]/2 = 172,5 кДж.
Пример 5. Расчет стандартной энтальпии химической реакции при различных температурах.
Рассчитайте стандартный тепловой эффект изобарно-изотермической реакции
С(к) + СО2(г) = 2СО(г)
при 298 К и при 1000 К, считая постоянными теплоемкости реагентов в данном температурном интервале.
Решение. Запишем значения стандартной энтальпии образования и стандартной теплоемкости веществ согласно данным (Приложение 2, [1]):
Вещество Δ fН 0298,кДж/моль С 0 р 298, Дж/моль.К
С(графит) 0 8,54
СО2 (г) −393,5 37,41
СО (г) −110,5 29,14
Для расчета энтальпии химической реакции при с.с. и 298 К воспользуемся следствием из закона Гесса:
Δ rН 0298= ∑ν i Δ f Н 0298, продуктов − ∑ν j Δ f Н 0298, исх веществ ;
Δ rН 0298 = 2Δ fН 0298СОг − Δ fН 0298Ск − Δ fН 0298СО2г = 2(−110,5) – 0 – (−393,5) =
= 172,5 кДж. Так как Δ rН 0298 > 0, данная реакция эндотермическая.
Зависимость энтальпии реакции от температуры в области 298 ÷ Т, в которой нет фазовых переходов, в интегральном виде выражается уравнением Кирхгофа:
Т
∆ rH 0 T = ∆ rH 0298 + ∫ ∆ rС 0 pdT,
298
где ∆rН0 298 − стандартная энтальпия реакции при 298К; ∆rСp0 − изменение стандартной теплоемкости системы в ходе реакции.
Если пренебречь зависимостью Ср реагирующих веществ от Т, то есть
∆rС0p = const, то имеем приближение в виде:
∆rН0Т = ∆rН0298 + ∆rС0р(Т − 298),
рассчитать ∆С0р можно по справочным данным, как разность стандартных изобарных теплоемкостей продуктов и исходных веществ при 298 К.
Рассчитаем изменение теплоемкости системы в результате реакции:
∆ rС 0 р = 2 С 0 р 298СОг – С 0 р 298Ск – С 0 р 298СО2г = 2(29,14) – 8,54 – 37,41 = 12,33 Дж/К.
По уравнению
∆rН0Т = ∆rН0298 + ∆rС0р(Т − 298)
рассчитаем энтальпию химической реакции при с.с. и 1000 К:
∆ rН 01000 = 172,5 + 12,33·10−3(1000 − 298) = 172,5 + 8,66 = 181,16 кДж.
Из расчетов следует, что при изменении температуры на 702 К увеличение теплового эффекта составляет всего около 5%.
Пример 6. Расчет тепла, выделенного в результате химической реакции.
Определите энтальпию процесса конденсации воды. Рассчитайте, сколько тепла выделится при образовании 1 м3 жидкой воды из пара при стандартных состояниях вещества.
Решение. Конденсация – это процесс перехода из газообразного состояния в жидкое, который относится к фазовым превращениям. Запишем уравнение конденсации для воды:
Н2О(г) = Н2О(ж).
Энтальпию этого превращения рассчитываем по следствию из закона Гесса, используя данные табл. (Приложение 2, [1]):
Δ rН 0298= ∑ν i Δ f Н 0298, продуктов − ∑ν j Δ f Н 0298, исх веществ ;
∆ rН 0298 = ∆ fН 0298Н2Ож – ∆ fН 0298Н2Ог = −285,84 – (−241,84) = −44 кДж.
Так как Δ rН 0298 < 0, процесс конденсации экзотермический.
Энтальпии химической реакции Δ rН равна тепловому эффекту этого процесса, протекающего в изобарно-изотермических условиях (Qp,T):
Qp,T = - Δ rHТ.
Определим количество вещества Н2О, содержащееся в 1 м3. Так как плотность воды ρ = 1 г/см3, то масса 1м3 воды: m = ρ V = 1·106 г.
Количество молей Н2О νН2О = m /MН2О = 106/18 = 5,56·104 моль.
Поскольку при конденсации 1 моля воды выделяется 44 кДж тепла, то при конденсации 5,56·104 молей выделится
Q = 44·5,56·104 = 2,45·106 кДж тепла.
Пример 7. Расчет удельной теплоты сгорания газового топлива.
Вычислить удельную теплоту сгорания газового топлива, содержащего 60% Н2 и 40% СН4, если известны теплоты сгорания газов: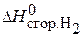 
= –286 кДж/моль; 
= –890 кДж/моль.
Решение. Термохимические уравнения процессов сгорания водорода и метана:
Н2(г) + ½О2(г) → Н2О(ж); 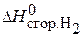= –286 кДж/моль;
СН4(г) + 2О2(г) → СО2(г) + 2Н2О(г); = –890 кДж/моль.
Теплота сгорания топлива может быть рассчитана по следствию из закона Гесса:
Δ rН 0 Т = ∑ν i Δ fНi 0 продуктов − ∑ν j Δ fНj 0исх веществ .
Удельная теплота сгорания газа QТ равна количеству теплоты, выделяющейся при сгорании 1м3 газообразного вещества до образования высших оксидов.
По условию задачи 1м3 данного газового топлива содержит 600 л Н2 и 400 л СН4, что составляет соответственно 600/22,4 молей Н2 и 400/22,4 молей СН4. (использовали молярный объем газа при нормальных условиях 22,4 л/моль).
В соответствии с уравнением:
Q т = –D Н сгор×(1000/22,4),
рассчитаем удельную теплоту сгорания газового топлива:
Q т = 286×(600/22,4) + 890×(400/22,4) = 7660,7 + 15892,8 = 23550 кДж/м3.
П 6. Расчет энтропии химической реакции. Расчет энергии Гиббса.
Определение термодинамической возможности самопроизвольного протекания химической реакции в заданном направлении. Определение температурной области самопроизвольного протекания химической реакции.
Пример 1. Расчет стандартной энтропии химической реакции при различных температурах.
Рассчитайте стандартную энтропию химической реакции
С(к) + СО2(г) = 2СО(г)
при 298 К и при 1000 К, считая постоянными теплоемкости компонентов в рассматриваемом температурном интервале.
Решение. Энтропия S – функция состояния системы, которая служит мерой неупорядоченности этой системы, измеряется в Дж/(моль·К).
Согласно данным табл. (см. Приложение IV, [2]; Приложение 4, [3]):
Вещество f S 0298, Дж/(моль·K) С 0 р 298, Дж/(моль·К)
С(графит) 5,74 8,54
СО2 (г) 213,68 37,41
СО (г) 197,54 29,14
Стандартная энтропия химической реакции при с.с. ( и моль/л) и 298 К, обозначается ∆ rS 0298 и рассчитывается по уравнению (следствие из закона Гесса):
Δ rS 0298 = ∑ν i fS 0298, i продуктов − ∑ν j fS 0298, j исх. веществ,
где f S 0298 - стандартная энтропия образования веществ при 298 К (см. Приложение IV, [2]; Приложение 4, [3]); ν i - стехиометрические коэффициенты уравнения химической реакции.
Рассчитаем:
Δ rS 0298 = 2 S 0298,СОг − S 0298,Ск − S 0298,СО2г = 2(197,54) – 5,74 – 213,68 =
= 175,66 Дж/K.
То есть данная реакция при 298 К идет с увеличением энтропии, что и следовало ожидать, так как число молей газообразных веществ в результате реакции увеличивается.
Зависимость энтропии реакции от температуры в области 298 ÷ Т, в которой нет фазовых переходов, в интегральном виде выражается уравнением
Т
∆ rS 0 T = ∆ rS 0298 + ∫ (∆ rС 0 p/Т) dT,
298
где ∆ rS 0298 − стандартная энтропия реакции при 298 К; ∆ rС 0 p − изменение суммарной стандартной теплоемкости системы в ходе реакции.
Рассчитаем изменение стандартной теплоемкости системы в результате реакции:
∆ r С 0 р = 2 С0р 298СОг – С0р 298Ск – С0р 298СО2г = 2.(29,14)–8,54–37,41 =12,33 Дж/К.
Для многих реакций можно пренебречь зависимостью Ср реагирующих веществ от Т, то есть ∆ rС 0 p = const. Тогда имеем приближение в виде:
∆ rS 0 T = ∆ rS 0298 + ∆ rС 0 р (ln Т − ln298).
По этому уравнению рассчитаем
∆ rS 01000 = 175,66 + 12,33ln(1000/298) = 175,66 + 14,93 = 190,59 Дж/К.
Как следует из расчетов, увеличение энтропии реакции, обусловленное ростом суммарной теплоемкости системы, при изменении температуры на 702 К составляет около 8,5%.
Пример 2. Расчет энергии Гиббса химической реакции при стандартном состоянии и различных температурах. Возможное направление самопроизвольного протекания процесса.
Рассчитайте стандартную энергию Гиббса химической реакции
С(к) + СО2(г) = 2СО(г)
при 298 К и при 1000 К. Сделайте вывод о возможности самопроизвольного протекания этой реакции при указанных температурах и стандартных состояниях всех компонентов.
Решение. Направление любого процесса определяется соотношением энтальпийного ∆ rН и энтропийного Т ∆ rS факторов реакции.
Энергия Гиббса,или свободная энергия G - функция состояния системы, учитывающая совместное влияние этих факторов, G = H – TS.
Однозначный критерий возможности самопроизвольного протекания реакции в прямом направлении в изобарно-изотермических условиях:
∆ rGТ = (∆ rHТ – T ∆ rSТ) < 0.
1). Для начала, будем считать, чтоэнтальпия и энтропия реакции не зависят от температуры. В широком интервале температур в первом приближении можно считать неизменной величину стандартной теплоемкости веществ в ходе химической реакции ∆ rС 0 p = 0, тогда
∆ rН 0 T = ∆ rН 0298 и ∆ rS 0 T = ∆ rS 0298 .
Для расчета применим приближенную формулу расчета энергии Гиббса
∆ rG 0 Т = ∆ rH 0298 − T ∆ rS 0298.
Используем данные, полученные в Примере 1. (Δ rS 0298 = 175,66 Дж/K) и в Примере 5. предыдущего практического занятия (Δ rН 0298 = 172,5 кДж).
∆ rG 0298 = 172,5 – 298 · 175,66·10−3 = 120,15 кДж, то есть ∆ rG 0298> 0;
∆ rG 01000 = 172,5 – 1000 · 175,66 · 10−3 = −3,16 кДж, то есть ∆ rG 01000 < 0.
Таким образом, при 298 К и стандартных состояниях веществ самопроизвольное протекание указанной реакции в прямом направлении невозможно (энтальпийный фактор не способствует самопроизвольному протеканию прямой реакции и определяет знак энергии Гиббса реакции при низких температурах). При высоких температурах определяющим становится энтропийный фактор реакции, он определяет отрицательное значение энергии Гиббса реакции при 1000 К и, следовательно, возможность самопроизвольного протекания реакции при этой температуре и стандартных состояниях компонентов.
2). Для более точного расчета ∆ rG 01000сначала рассчитаем изменение стандартной теплоемкости системы в ходе реакции:
∆ r С 0 р = 2 С0р 298СОг – С0р 298Ск – С0р 298СО2г = 2.(29,14)–8,54–37,41 =12,33 Дж/К.
Значение стандартной ∆rG 0 Т для любой температуры Т можно в общем случае рассчитать с использованием справочных данных по уравнению:
Т Т
∆ rG 0 Т = ∆ rH 0 Т −T ∆ rS 0 Т = ∆ rH 0298 + ∫ ∆ rС 0 pdT - Т ∆ rS 0298 - Т ∫ (∆ rС 0 p/T) dT.
298 298
Для многих реакций можно пренебречь зависимостью Ср реагирующих веществ от Т, то есть ∆ rС 0 p = const. Тогда имеем приближение в виде:
∆r G0T = ∆ r H 0 Т −T ∆ rS 0 Т = ∆r Н0 298 + ∆ rс 0 р (Т - 298)– Т .∆ r S0 298– T . ∆ rС 0 р (ln Т − ln298).
Для расчета ∆ rG 01000используем это приближение:
∆r G0T = ∆ r H 0 Т – Т .∆ r S0Т = ∆r Н0 298 + ∆ rс 0 р (Т - 298)– Т .∆ r S0 298 – Т .∆ r с0р ln (Т/ 298).
Δ r Н0 298 = 172,5 кДж, ∆rS0 298 = 175,66 Дж/К.
∆r G0 1000 =172,5 +12,33.10-3. (1000-298) - 1000. 175,66.10-3 - 1000.12,33.10-3. ln (1000/298) =
= -9,43 кДж, то есть ∆ rG 01000 < 0.
Как видно, имеется различие в значениях стандартной энергии Гиббса ∆ rG 0 T, рассчитанной по разным методикам.
Пример 3. Определение температурной области самопроизвольного протекания реакции.
Определите температурную область самопроизвольного протекания реакции
С(к) + СО2(г) = 2СО(г)
при стандартных состояниях компонентов.
Решение. Реакция может протекать самопроизвольно при стандартных состояниях компонентов в определенной области температур, для которых ∆rG 0 Т < 0.Чтобы найти эту область температур нужно определить граничную температуру (температуру равновесия), при которой значение ∆rG 0 Т меняет знак, то есть необходимо решить неравенство относительно Т:
∆ rG 0 Т = ∆ rH 0298 + ∫ Т 298∆ rС 0 pdT + Т ∆ rS 0298 + Т ∫ Т 298(∆ rС 0 p/T) dT < 0.
Если пренебречь зависимостью ∆ rH 0 и ∆ rS 0от температуры, то граничную температуру (температуру равновесия) можно определить из приближенного неравенства:
∆ rG 0 Т = ∆ rH 0298 − T ∆ rS 0298< 0.
Подставляя в это выражение значения Δ rН 0298 = 172,5 кДж и
Δ rS 0298 = 175,66 Дж/K, (см. Пример 3), получаем:
∆ rG 0 Т =(172,5 – Т · 175,66·10−3) < 0.
Откуда Т > 982 К. Верхним пределом искомой температурной области является предел существования наименее устойчивого компонента реакции, который находится из справочных данных.
Вещество Температурный интервал, К
С(графит) 298 ÷ 2300
СО2 (г) 298 ÷ 2500
СО (г) 298 ÷ 2500
Как следует из полученных данных, искомой областью температур, в которых возможно самопроизвольное протекание данной реакции при стандартных состояниях, является интервал Т = 982÷2300 К.
Пример 4. Расчет энергии Гиббса химической реакции при нестандартных парциальных давлениях газообразных компонентов реакции.
Определите, при каком соотношении парциальных давлений газообразных компонентов реакции
С(к) + СО2(г) = 2СО(г)
возможно ее протекание в прямом направлении при 298 К?
Решение. Связь между Δ rGT (при любых давлении и температуре) и ∆ rG 0 T (при с.с. и любой температуре) выражается уравнением изотермы Вант Гоффа,которая для реакции
a A(г) + b B(г) + d D(к) = e E(г) + f F(г)
имеет вид: Δ rGТ = ∆ rG 0 Т + RT ln(pe E pf F/ pa A pb B),
где р i – относительные парциальные давления соответствующих газообразных компонентов реакции.
Возможность самопроизвольного протекания данной реакции в прямом направлении при 298 К определяется неравенством Δ rG 298 < 0, в котором энергия Гиббса реакции рассчитывается по уравнению изотермы Вант Гоффа.
Для заданной реакции изотерма Вант Гоффа имеет вид:
Δ rG 298=[ ∆rG 0 298 + RT ln(p 2CO/ p CO2)] < 0.
Подставляя ∆rG 0298=120,15 кДж, (см. в Примере 2), получаем неравенство:
120,15 + 8,31·10−3·298 ln(p 2CO/ p CO2) < 0.
Найдем соотношение давлений СО и СО2, при котором это неравенство выполняется. Решаем неравенство и получаем: ln(p 2CO/ p CO2) < −48,5,
откуда p 2CO/ p CO2 < 10−21.
Пример 5. Расчет энергииГиббса химической реакции по закону Гесса.
Рассчитайте стандартную энергию Гиббса химической реакции при
298 К
С(к) + СО2(г) = 2СО(г), (1),
если известны значения энергии Гиббса следующих реакций:
С(к) + О2(г) = СО2(г), ∆ rG 0298 = −394,37 кДж; (2);
Fe(к) + CО2(г) = FeO(к) + CO(г), ∆ rG 0298= 12,92 кДж; (3);
2Fe(к) + O2(г) = 2FeO(к), ∆ rG 0298= −488,6 кДж; (4).
Решение. Согласно закону Гесса, энергия Гиббса реакции не зависит от числа промежуточных стадий и веществ, в результате которых получена эта реакция. Для того, чтобы получить уравнение реакции (1), нужно сложить уравнение реакции (2) и удвоенное уравнение реакции (3) и вычесть уравнение реакции (4). Для определения энергии Гиббса реакции (1) те же действия нужно проделать со значениями ∆rG 0298соответствующих реакций. Тогда
∆ rG 01 = ∆ rG 02 + 2∆ rG 03 −∆ rG 04 = −394,37 + 2(12,92) –(−488,6) = = 120,1 кДж.