Решение задачи (1.3), (1.4) для детерминированных ДС, в частном случае для ДС (1.1) с ограничениями на управление (1.2), предлагается строить на основе принципа максимума Понтрягина [1, 2, 3], в терминологии читаемого курса лекций - принципа минимума.
В связи с тем, что данная КР должна прививать навыки оптимизации программного управления для ДС и критериев оптимизации общего вида, включая нелинейные варианты, методика и алгоритм решения задачи оптимального управления рассматривается для более общей постановки задачи.
Задача: определить оптимальную программу управления u(∙)Î Ut (1.2) системой:
 = f(x, u), x(t0) = x0, = f(x, u), x(t0) = x0,
| (2.1) |
обеспечивающее минимум критерию:
Jобщ =  f 0(x(t), u(t)) dt + F (x(tk)) f 0(x(t), u(t)) dt + F (x(tk))
| (2.2) |
при ограничениях на величину управления:
| u(t) Î Uextr Uextr = { u(∙)Î Ut: umin ≤ u(t) ≤ umax } | (2.3) |
Здесь х – вектор фазового состояния ДС, имеющий в общем случае размерность [n´1]; х0 – вектор фазового состояния ДС в начальный момент времени - t0 из ограниченного интервала времени движения ДС – [t0, tk], tk - конечный момент времени движения ДС; u – вектор управления ДС, имеющий в общем случае размерность [r´1]; f(x, u) – детерминированная вектор-функция правых частей ДС, непрерывная и дифференцируемая по своим аргументам, имеющая размерность [n´1]; f 0(x, u) – детерминированная скалярная функция вектора фазового состояния ДС - х и вектора управления ДС - u, непрерывная и дифференцируемая по своим аргументам; F (x(tk)) - детерминированная скалярная терминальная функция вектора конечного фазового состояния ДС - х(tk), также непрерывная и дифференцируемая по своим аргументам.
Формально эта постановка задачи может быть переписана более компактно:
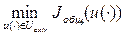
| (2.4) |
В практическом приложении методику решения поставленной задачи целесообразно представить в виде следующего расширенного алгоритма.
1) Формирование функции Гамильтона (гамильтониана).
Для ДС (2.1) и критерия оптимальности (2.2) функция Гамильтона будет иметь вид [2, 3, 4]:
| H(x, u, ψ) = f 0(x(t), u(t)) + ψ(t)T∙ f(x(t), u(t)) | (2.5) |
где ψ(t) - вектор сопряженных функций, размерности [n´1].
В частном случае, для ДС (1.1) функция Гамильтона будет следующей.
| H(x, u, ψ) = xT(t) Q x(t) + uT(t) W u(t) + ψ(t)T∙ [A x(t) + B u(t)] | (2.6) |
Соответственно, в общем случае вектор сопряженных функций определяется как результат интегрирования системы дифференциальных уравнений:
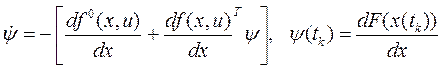
| (2.7) |
Где F(x(tk)) – терминальная часть критерия оптимальности общего вида (2.2)
В частном случае (для линейной ДС (1.1) и критерия (1.3)), система дифференциальных уравнений, определяющая сопряженный вектор ψ(t), будет иметь вид:

| (2.8) |
Из систем уравнений (2.7) (2.8) видно, что они обе зависят как от самого сопряженного вектора ψ (t), так и от вектора х (t). В связи с этим ни та, ни другая системы не могут быть проинтегрированы без учета информации о поведении вектора фазового состояния х (t) в процессе изменения вектора ψ (t). Кроме того, в общем случае для уравнений (2.7) это невозможно сделать без информации о поведении вектора управления u (t) в процессе движения системы t Î[ t0, tk ].
Согласно [2, 4], вся требуемая информация может быть получена в результате:
· применения необходимых условий оптимальности в форме принципа минимума (в терминологии читаемого курса лекций),
· совместного решения систем дифференциальных уравнений для вектора фазового состояния х (t) и сопряженного вектора ψ (t), которые при их объединении называются системой канонических уравнений [2] и имеют общую размерность [2 n ´1].
2) Применение необходимых условий оптимальности в форме принципа минимума
В соответствии с теорией оптимального управления программная стратегия оптимального управления должна удовлетворять для ДС (2.1), критерия оптимальности (2.2) и при ограничениях (2.3) следующим необходимым условиям в форме принципа минимума [2].
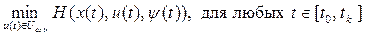
| (2.9) |
В результате проведения процедуры минимизации гамильтониана на всем интервале времени движения системы t Î[ t0, tk ] можно получить структуру оптимального программного управления:
| u((∙), x(∙), ψ(∙)) = { u((t), x(t), ψ(t)), tÎ[t0, tk] } | (2.10) |
Как видно из (2.10), хотя структура оптимального программного управления является сложной функцией времени, однако в промежуточных преобразованиях она зависит также от вектора текущего состояния ДС - х(t) и текущего сопряженного вектора - ψ(t).
В частном случае, для рассматриваемых ДС (1.1) и критерия (1.3), необходимые условия в форме принципа минимума могут быть представлены в более простом и конкретном виде. Это становится возможным поскольку:
- во-первых, в частной постановке задачи (1.1) – (1.4) на управление не накладывается прямых ограничений, таких как в (2.3), и операция минимизации гамильтониана по управлению сведется к применению необходимых условий его минимума по управлению, то есть обнулению частной производной гамильтониана по управлению:
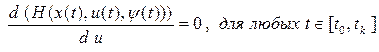
| (2.11) |
- во-вторых, в силу конкретности вида функции Гамильтона (2.6) и (2.11), структура оптимального программного управления может быть получена в конкретном виде.
После взятия частной производной гамильтониана (2.6) по управлению можно получить:
| 2 W u(t) + ψ(t)T∙B = 0 | (2.12) |
Откуда следует, что структура оптимального программного управления для рассматриваемой частной задачи будет иметь вид:
u(∙) = - 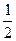 W-1 B T∙ψ(∙) = {u(t) = - W-1 B T∙ψ(∙) = {u(t) = - 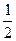 W-1 B T∙ψ(t), tÎ[t0, tk]} W-1 B T∙ψ(t), tÎ[t0, tk]}
| (2.13) |
Однако, также как в общем случае (2.10) структура оптимального программного управления (2.13) зависит от поведения текущего сопряженного вектора - ψ(t), tÎ[t0, tk].
3) Определение оптимального программного управления путем решения краевой задачи для канонической системы дифференциальных уравнений
В общем случае для задачи (2.1) – (2.4) каноническая система дифференциальных уравнений будет иметь вид:
 = f(x, u), x(t0) = x0 = f(x, u), x(t0) = x0
| (2.14) |
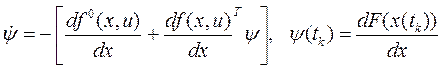
| (2.15) |
Общая размерность системы (2.14), (2.15) будет [2n ´ 1].
Принципиально важной особенностью этой системы является то, что первая система (2.14) «привязана» к вектору начального состояния x(t0) (на «левом» конце траектории), а вторая система (2.15), которую необходимо интегрировать совместно с первой, задана в момент окончания движения ψ(tk) (на «правом» конце траектории).
Учитывая эту особенность системы (2.14), (2.15), для определения траектории оптимального движения системы (2.1) - x(∙) и соответствующего сопряженного вектора ψ(∙), необходимых для окончательного определения оптимальной программы управления (см. (2.10)), требуется решить краевую задачу, удовлетворяющую заданным условиям на обоих концах траектории.
В общем случае для достижения этой цели предлагается на «правом» конце траектории сформировать функцию невязки, зависящую от неизвестных начальных значений сопряженного вектора ψ(t0), как от параметров минимизации функции невязки. Предлагается также, связь между этой функцией и параметрами установить путем численного интегрирования канонической системы уравнений (2.14), (2.15), то есть:
| Φ(tk , ψ(t0)) = [ψинт(tk, ψ(t0)) - ψ(tk)]2 | (2.16) |
Где Φ(tk , ψ(t0)) – функция невязки, вычисляемая в конечный момент времени tk; ψинт(tk, ψ(t0)) - сопряженный вектор, получаемый как результат численного интегрирования системы (2.14), (2.15) при начальных условиях х(t0), ψ(t0); ψ (tk) – требуемое конечное значение сопряженного вектора, вычисляемое согласно (2.15) по формуле:  .
.
Минимизация невязки (2.16) должна осуществляться итеративно с помощью одного из методов математического программирования нулевого порядка. Очевидно, что для каждой новой итерации необходимо заново интегрировать уравнения (2.14), (2.15) с новыми значениями ψi(t0).

| (2.17) |
Рекомендуется использовать один из методов математического программирования, реализованный в рамках курсовой работы по дисциплине: «Методы оптимизации» [10].
4) Решение краевой задачи в случае линейной канонической системы дифференциальных уравнений
В частном случае для задачи (1.1) – (1.4) каноническая система дифференциальных уравнений будет иметь линейный вид (см. (1.1) (2.8)):
 = A x + B u, x(t0) = x0 = A x + B u, x(t0) = x0
| (2.18) |

| (2.19) |
А с учетом полученной с помощью необходимых условий структуры оптимального программного управления u = - 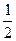 W-1 BT∙ψ (см. (2.13)), каноническая система примет замкнутый вид:
W-1 BT∙ψ (см. (2.13)), каноническая система примет замкнутый вид:
 = A x - = A x - 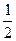 B W-1 BT ψ, x(t0) = x0 B W-1 BT ψ, x(t0) = x0
| (2.20) |

| (2.21) |
Если ввести новый, расширенный вектор состояния системы:
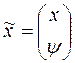 , ,
| (2.22) |
тогда уравнения (2.20), (2.21) могут быть переписаны более компактно:

| (2.23) |
где матрица 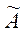 размера [2n ´ 2n] составлена из следующих блоков.
размера [2n ´ 2n] составлена из следующих блоков.
 , ,
| (2.24) |
Исходя из (2.20) и (2.21), краевые условия для расширенной системы (2.23) с учетом новых обозначений можно записать в виде:
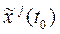 = x j0, j = 1,n = x j0, j = 1,n
| (2.25) |
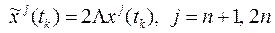
| (2.26) |
Решение краевой задачи (2.23) – (2.26) может быть получено аналитически с применением формализма фундаментальной (переходной) матрицы [2, 4].
Пусть Φ(t, t0) - фундаментальная матрица решений системы линейных уравнений (2.23). Это означает, что она должна удовлетворять следующему матричному дифференциальному уравнению.

| (2.27) |
где I2n - единичная матрица размера [2n ´ 2n].
Тогда общее решение системы (2.23) можно представить в виде:
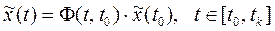
| (2.28) |
Разбивая фундаментальную матрицу Φ(t,t0) на четыре угловых блока, имеющих одинаковые размеры [n ´ n], а именно: Φ11(t,t0), Φ12(t,t0), Φ21(t,t0), Φ22(t,t0), можно получить развернутое решение системы (2.23):
| x(t)= Φ11 (t, t0)∙x(t0) + Φ12 (t, t0)∙ψ(t0) | (2.29) |
| ψ(t)= Φ12 (t, t0)∙x(t0) + Φ22 (t, t0)∙ψ(t0) | (2.30) |
Таким образом, появляется возможность с помощью соотношения (2.30) получить аналитическую связь краевых условий для сопряженного вектора.
| ψ(tk)= Φ12 (tk, t0)∙x(t0) + Φ22 (tk, t0)∙ψ(t0) | (2.31) |
Согласно принятым правилам построения сопряженного вектора ψ(t) его первообразные «привязываются» к конечному состоянию [2, 3], которое для рассматриваемой линейной системы имеет вид (см. (2.21)):

| (2.32) |
Имея это ввиду, можно с помощью (2.31) и (2.29) определить соответствующее конечному состоянию сопряженного вектора ψ(tk) начальное его состояние ψ(t0):
| ψ(t0)= - [Φ22 (tk, t0)- 2Λ∙ Φ12 (tk, t0) ]-1 ∙[Φ21 (tk, t0) - 2Λ∙ Φ11 (tk, t0)∙]∙ x(t0) | (2.33) |
Теперь векторы аналитических решений x(t) и ψ(t) канонической системы (2.17), (2.18) могут быть поставлены в зависимости только от начального состояния вектора состояния x(t0):
| x(t)= [Φ11 (t, t0) – 2∙Φ12 (t, t0)∙K(tk, t0)]∙x(t0) | (2.34) |
| Ψ(t)= [Φ21 (t, t0) – 2∙Φ22 (t, t0) K(tk, t0)]∙x(t0) | (2.35) |
где матрица K(tk, t0) размера [n ´ n] имеет вид:
| K(tk, t0)= 1/2 [Φ22 (tk, t0)- 2Λ∙ Φ12 (tk, t0) ]-1 ∙[Φ21 (tk, t0) - 2Λ∙ Φ11 (tk, t0)] | (2.36) |
В соответствии со структурой оптимального управления (2.13), полученной с помощью необходимых условий (2.11), оптимальное программное управление линейной системой (1.1) может быть представлено в виде:
u(t) = W-1 B T∙[ Φ22 (t, t0) K(tk, t0) - 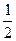 Φ21 (t, t0)]∙x(t0),
tÎ[t0, tk] Φ21 (t, t0)]∙x(t0),
tÎ[t0, tk]
| (2.37) |
Таким образом, в итоге определено аналитическое решение задачи оптимизации программного управления линейной динамической системой (1.1) по смешанному квадратичному критерию (1.3).