Фундаментальная (переходная) матрица линейной детерминированной динамической системы с постоянными коэффициентами имеет ряд основополагающих свойств, которые могут быть использованы при ее построении.
Рассмотрим однородную систему линейных дифференциальных уравнений с постоянными коэффициентами типа (2.23):
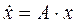
| (2.38) |
где x – вектор размера [n ´ 1], А – матрица с постоянных по времени коэффициентов, размера [n ´ n].
Пусть в начальный момент времени движения t0 система (2.38) находится в состоянии
| x(t0) = x0 , | (2.39) |
а время движения ограничено моментом tk ≤ M < ∞.
Тогда система (2.38) имеет фундаментальную матрицу решений, с помощью которой может быть получено фазовое состояние системы в любой момент времени t Î [t0, tk], то есть
| x(t) = Φ (t, t0) x(t0) | (2.40) |
где Φ (t, t0) – фундаментальная матрица решений системы (2.38),
размера [n ´ n].
Фундаментальная матрица Φ (t, t0) имеет следующие свойства [4].
1. В начальный момент движения системы фундаментальная матрица должна превращаться в единичную матрицу, размера [n ´ n]:
| Φ (t0, t0) = In | (2.40) |
2. Обращенная фундаментальная матрица должна быть эквивалентна фундаментальной матрице движения в «обратном» времени:
| Φ-1 (t, t0) = Φ (-t, t0) | (2.41) |
3. Как отмечалось выше в (2.27), фундаментальная матрица должна удовлетворять матричному дифференциальному уравнению:
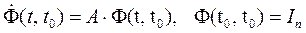
| (2.42) |
Из указанных свойств следует, что фундаментальная матрица может быть получена как общее решение однородной системы линейных дифференциальных уравнений (2.38) с начальными условиями, заданными единичной матрицей (2.40).
Алгоритм:
1) Частное решение системы (2.38) представляется в виде
| xi(t) = β i ∙exp(r∙(t – t0)) | (2.43) |
где xi(t) – i -ая координата вектора x, размера [n ´ 1], β i – неизвестные коэффициенты, подлежащие определению; r – показатель степени экспоненты, также, подлежащий определению.
2) Формируется система алгебраических уравнений путем подстановки частного решения (2.43) в систему (2.38) и последующего деления правой и левой части системы на множитель exp(r∙(t - t0)) > 0. В результате получается конкретная однородная система алгебраических уравнений вида:
| (a11 - r) β 1 + a12 β 2 +……....+ a1n β n = 0 a21 β 1 + (a22 - r) β 2 +..….+ a2n β n = 0 ………………………………………………… an1 β 1 + an2 β 2 +….+ (a2n – r)β n = 0 | (2.44) |
3) Для обеспечения нетривиального решения однородной системы алгебраических уравнений (2.44) относительно коэффициентов β j её определитель должен быть равен нулю [12], то есть:

| (2.45) |
4) При раскрытии определителя (2.45) формируется характеристическое уравнение n –ой степени r (показателя степени экспоненты).
5) Каждый из n корней характеристического уравнения определяет одно из частных решений уравнений (2.38) и после подстановки одного из них, например r(1), в систему (2.44) можно получить соотношения, связывающие коэффициенты β i (1), i=1,n с точностью до умножения на константу:
| (a11 - r(1)) β 1 (1)+ a12 β 2(1) +……....+ a1n β n(1) = 0 a21 β 1(1) + (a22 - r(1)) β 2(1) +..….+ a2n β n(1) = 0 .……………………………………………………….. an1 β 1(1) + an2 β 2(1) +….+ (a2n – r(1))β n(1) = 0 | (2.46) |
Другими словами, можно получить частные решения xi(1) (t) для i=1,n координат с точности до константы С(1), т.е. (2.46) даёт возможность выразить одни коэффициенты β i (1) через другие коэффициенты с точностью до умножения на константу С(1):
| xi(1) (t) =С(1) β i (1)∙exp(r(1) ∙(t – t0)), i=1,n | (2.47) |
Аналогичные результаты могут быть получены для всех остальных корней характеристического уравнения, т.е.
| xi(j) (t) =С(j) β i (j)∙exp(r(j) ∙(t – t0)), i=1,n, j=1,n | (2.48) |
Здесь все коэффициенты β i (j), i=1,n имеют конкретные числовые значения, полученные из (2.46), а константы С(j), j=1,n подлежат определению из начальных условий при t = t0 для (2.38).
6) Общее решение системы линейных дифференциальных уравнений складывается из полученных частных:
| x1(t) = C(1) β 1 (1)exp(r(1)(t – t0)) + C(2) β 1 (2)∙exp(r(2)(t – t0)) + … + C(n) β 1 (n)exp(r(n)(t – t0)) x2(t) = C(1) β 2 (1)exp(r(1)(t – t0)) + C(2) β 2 (2)∙exp(r(2)(t – t0)) + … + C(n) β 2 (n)exp(r(n)(t – t0)) ………………………………………………………………………. xn(t) = C(1) β n (1)exp(r(1)(t – t0)) + C(2) β n (2)∙exp(r(2)(t – t0)) + … + C(n) β n (n)exp(r(n)(t – t0)) | (2.49) |
7) Строится фундаментальная матрица Φ (t, t0), которая согласно своим свойствам в начальный момент времени t0 должна превращаться в единичную матрицу In (см.(2.40)).
То есть коэффициенты C(j k) для k -го столбца фундаментальной матрицы должны определяться из условий:
| C(j1) β 1 (1)+ C(j2) β 1 (2)+ …+ C(jn) β 1 (n) = 0 C(j1) β 2 (1)+ C(j2) β 2 (2)+ …+ C(jn) β 2 (n) = 0 ………………………………………………..… C(j1) β k (1)+ C(j2) β k (2)+ …+ C(jn) β k (n) = 1 ………………………………………..………… C(j1) β n (1)+ C(j2) β n (2)+ …+ C(jn) β n (n) = 0 | (2.50) |
Таким образом, получая набор значений коэффициентов C(j k), j=1,n для начальных условий, образованных единичной матрицей, то есть для всех k от 1 до n можно по столбцам сформировать фундаментальную матрицу Φ (t, t0), соответствующую, линейной детерминированной динамической системе с постоянными коэффициентами (2.38).
Варианты Заданий к курсовой работе
Как отмечалось, коэффициенты матриц линейной ДС (1.1) в сочетании с варьируемыми «весовыми» коэффициентами смешенного квадратичного критерия (1.3) позволяют существенно видоизменять вид процесса движения линейной ДС посредством оптимального управления u (·) (1.2). В связи с этим управляемое движение ДС (даже для одинаковых ДС!) будет сильно отличаться в зависимости от значимости важнейших характеристик процесса движения, которая им придается с помощью «весовых» коэффициентов квадратичного критерия оптимальности.
Обе части работы, аналитическая и численная, имеют одинаковые исходные данные, отличающиеся по вариантам заданий, кроме:
t 0 = 0 сек,
tk = 4 сек (для всех вариантов одинаковые).
Остальные данные вводятся по таблице 3.1 согласно следующим обозначениям:
 ,
,  ,
,  , W=w,
, W=w, 
Таблица 3.1
| № | a 12 | a 21 | a 22 | b | q 11 | q 22 | w | l 11 | l 22 |
| 1.5 | |||||||||
| 1.5 | |||||||||
| -0.02 | 0.2 | 0.4 | 0.2 | 0.8 | 0.1 | ||||
| -0.01 | 0.1 | 0.5 | 0.1 | 0.3 | 0.2 |