Выполнил:
студент группы __________________
________________________________
№ зачетки ______________________
Проверил: _______________________
Волгоград 20--
Начертательная геометрия изучает способы построения пространственных объектов на плоскости и способы решения задач геометрического по этим изображениям. Изображения, построенные по правилам, изучаемым в начертательной геометрии, позволяют представить мысленно форму предметов и их взаимное расположение в пространстве, определить их размеры, исследовать геометрические свойства, присущие изображаемому предмету.
Правила построения изображений, излагаемые в начертательной геометрии, основаны на методе проекций, который является основным методом в начертательной геометрии. Метод проекций состоит в том, что устанавливает связь между точками проецируемого объекта и точками плоскости, называемой плоскостью проекций.
Рассмотрение метода проекций начинают с построения проекций точки, так как построение изображения любого пространственного объекта включает в себя построение ряда точек, принадлежащих этому объекту.
Центральные и параллельные проекции
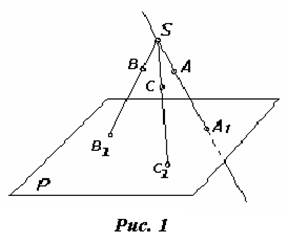
Представим в пространстве плоскость Р и точку S, не лежащую в этой поскости (рис. 1). Возьмем в пространстве некоторую точку А и проведем через точки А и S прямую до пересечения с плоскостью Р в точке А1. Точка А1 называется центральной проекцией точки А на плоскость Р, точка S – центром проекций, линия SA – проецирующей прямой или проецирующем лучом и плоскость Р – плоскостью проекций. Для нахождения проекций точек В и С (рис. 1) следует через взятые точки и центр проекций провести проецирующие прямые до пересечения их с плоскость. Р. Полученные точки В1 и С1 будут соответственно проекциями точек В и С.
|
|
Если центр проекций рассматривать как бесконечно удаленную точку, то при проецировании системы точек все проецирующие прямые оказываются параллельны между собою. Для их проведения должно быть указано некоторое направление проецирования (отмеченное стрелкой s на рис. 2). Построенная проекция называется параллельной. Таким образом, параллельной проекцией точки будем называть точку пересечения проецирующей прямой, проведенной параллельно заданному направлению, с плоскостью проекций.
Параллельные проекции делятся на косоугольные и прямоугольные ( или ортогональные). Для косоугольных проекций направление проецирования составляет с плоскость проекций угол, не равный 900, во втором случае проецирующие прямые перпендикулярны плоскости проекций.
Для однозначного определения положения точки в пространстве необходимо и достаточно иметь проекции на двух плоскостях проекций, но в инженерной практике при построении проекций различных предметов с целью полного выявления их формы часто используют больше двух плоскостей проекций. Поэтому рассмотрим построение проекций точки на трех плоскостях проекций (рис. 3, 4)
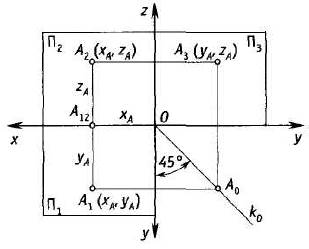
Рис. 3 Рис. 4
Одна из плоскостей проекций расположена горизонтально и называется горизонтальной плоскостью проекций, и обозначается П1. Проекции элементов пространства на ней обозначаются с индексом 1: А1, а1, … и называются горизонтальными проекциями (точки, прямой, плоскости).
Плоскость, расположенная перед наблюдателем, перпендикулярно первой, называется фронтальной плоскостью проекций, и обозначается П2. Проекции элементов пространства на ней обозначаются с индексом 2: А2, а2, … и называются фронтальными проекциями (точки, прямой, плоскости).
|
|
Плоскость, расположенная справа от наблюдателя перпендикулярно одновременно горизонтальной и фронтальной плоскостям проекций, называется профильной плоскостью проекций, и обозначается П3 . Проекции элементов пространства на ней обозначаются с индексом 3: А3, а3, … и называются профильными проекциями. Линию пересечения горизонтальной и фронтальной плоскостей проекций принимают за ось координат х. Линию пересечения горизонтальной и профильной плоскостей проекций принимают за ось координат у. Линию пересечения фронтальной и профильной плоскостей проекций принимают за ось координат z.
Для получения комплексного чертежа (или Эпюра Монжа - рис. 4) – за плоскость чертежа принимают фронтальную плоскость проекций П2 , горизонтальную плоскость проекций П1 совмещают с плоскостью чертежа вращением вокруг оси x, а профильную плоскость проекций П3 совмещают с плоскостью чертежа вращением вокруг оси z. Чертеж – это две (или более) проекции точки, совмещенные на одной плоскости (плоскости чертежа) и связанные линиями проекционной связи. Прямая А1-А2, соединяющая горизонтальную и фронтальную проекцию точки, называется вертикальной линией связи; прямая А2- А3 , соединяющая фронтальную и профильную проекции точки, называется горизонтальной линией связи.
Рассматривая чертеж точки, выделяют, что:
· две проекции точки принадлежат одной линии связи;
|
|
· линии связи перпендикулярны соответствующим осям координат;
· две проекции точки необходимо и достаточно для определения положения точки в пространстве, и две проекции точки определяют её третью проекцию.
Три основные плоскости проекций могут рассматриваться и как координатные плоскости, если точка задана координатами. Зная координаты точки можно построить её комплексный (рис. 4) и аксонометрический (рис. 5) чертеж.
Задачи