В результате очистки данных табл. 1.1 от грубых промахов получен ряд чисел, приведенный в таблице 1. 6. (N о – количество членов очищенного ряда)
Результат измерений после очистки от грубых промахов Таблица 1.6.
| № эл-та | 1 | 2 | 3 | … | … | n | |||
| значение | V1 | vv | vv | … | … | … | … | .. | .. |
| № эл-та | n+1 | n+2 | … | … | … | … | … | .. | n+m |
| значение | vv | vv | vv | ||||||
| № эл-та | n+m+ 1 | ….. | …. | …. | …. | N о | |||
| значение | vv | … | … | … | … | VNо |
Среднее по формуле (1.1)  = _____; N=_____; V ср=___/____=
= _____; N=_____; V ср=___/____=
Расчет дисперсии с этими данными произведен в таблице 1.7
Расчет данных для вычисления дисперсии Таблица 1.7
| i | (Vi-Vср)2 | i | (Vi-Vср)2 | i | (Vi-Vср)2 |
| …. | … | ||||
| … | … | Nо | |||
| Сумма | ,,,,, |
D= Сумма/ N о = _____/____=____
Остальные итоговые статистические характеристики также вычисляются по формулам, приведенным в п. 1.2.1:
Среднеквадратическое отклонение σ= 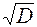 =
=  ____;
____;
Среднеквадратическое отклонение среднего σ0= σ/  =___/___=
=___/___=
Коэффициент Стьюдента (табл.1.4), и по формуле (1.6)
t ст N о= _____+  ε= t ст N о∙σ0 ____∙___= ____
ε= t ст N о∙σ0 ____∙___= ____
Окончательная оценка результатов измерения физической величины:
V = V ср ± ε =____ ±____
Относительная погрешность результата измерения составляет
 =____ ∙100/_____=______
=____ ∙100/_____=______
Сравнивая полученный результат с результатом для неочищенного ряда, можно сделать вывод, что …*/ надо сравнить и закончить вывод /*
ПОДБОР ЭМПИРИЧЕСКИХ ФОРМУЛ МЕТОДОМ
НАИМЕНЬШИХ КВАДРАТОВ
Задача подбора эмпирической формулы для эмпирической табличной функции относится к общематематической задаче аппроксимации табличных данных функциональной зависимостью. Наилучшим методом аппроксимации является метод наименьших квадратов, который состоит в том, функциональная зависимость выбирается такой, чтобы сумма квадратов отклонений табличных данных от функциональной зависимости была минимальной.
Наиболее просто находится линейная функциональная зависимость. Поэтому когда табличная функция явно не линейна, производится процедура линеаризации, позволяющая применить простейшие формулы метода.
Анализ исходной информации
Исходные данные приведены в «Задании на РГР» в начале работы. Они представляют собой N экспериментальных значений функции yi, полученные при изменении аргумента (фактора) xi в порядке его возрастания.
Для дальнейшей обработки эти данные представлены в табличной форме в «Excel е » в таблице 2.1, на основании таблицы построен исходный график эмпирической зависимости (рис. 2.1).
Исходные данные
Таблица 2.1
| № эксперим. точки i | Значение аргумента xi. | Значение функции yi | № эксперим. точки i | Значение аргумента xi. | Значение функции yi |
| х 1. | у 1 | … | … | ||
| … | … | …. | … | … | |
| … | … | … | …N | … xN. | yN |
 Рис. 2.1 График исходной функции (пример)
Рис. 2.1 График исходной функции (пример)
| Основные параметры исходной эмпирической зависимости: Количество опытов …N= ___ Максимальное значение фактора……. ………. хN. =___ Минимальное значение фактора……………… х1 =__. Максимальное значение функции …………. у А=_____ Максимальное значение функции ………….. у Б_____ (А и Б –номера max и min значений уi в таблице 2.1.) |