Основные теоремы теории вероятностей

Суммой A+B двух событий A и B называется событие, которое заключается в появлении события A или события B или обоих вместе.

Вероятность суммы несовместных событий A и B равна сумме вероятностей этих событий:

. (1.7)

Пример 1.14. В ходе исследования потребительского рынка проводили опрос потребителей. В частности, один из вопросов касался сорта зубной пасты, которую использует потребитель. Если известно, что 14% населения использует сорт A, а 9% – сорт B, то чему равна вероятность того, что случайно выбранный человек будет использовать одну из двух паст. (Предполагается, что в данный момент человек использует только одну пасту).

Решение. Пусть A – событие, состоящее в том, что выбранный человек использует пасту сорта A, а B – событие, состоящее в том, что выбранный человек использует пасту сорта B. Поскольку события A и B несовместные по условию задачи, то, используя теорему сложения вероятностей (1.7), получим

.

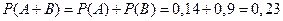Произведением событий A и B называется событие , состоящее в появлении одновременно обоих этих событий.

Вероятность произведения независимых событий A и B равна произведению вероятностей этих событий:

. (1.8)

Пример 1.15. Алмазы, возможно, вскоре станут использовать в качестве полупроводников в спутниках связи. Теория предсказывает, алмазные микросхемы будут более быстродействующими, термо- радиационностойкими, что особенно важно для приборов, работающих в космосе. По оценкам экспертов, вероятности этих трех событий равны 0,9; 0,9 и 0,95 соответственно. Предполагается, что обсуждением проекта по разработке алмазных микросхем стоит вести лишь в том случае, если имеется хотя бы 70% уверенности в том, что они будут обладать всеми тремя указанными свойствами. Должен ли обсуждаться проект?

Решение. Пусть A – событие, состоящее в том, что алмазные микросхемы будут более быстродействующими, B – событие, состоящее в том, что алмазные микросхемы будут более термостойкими, C – событие, состоящее в том, что алмазные микросхемы будут более радиационностойкими. Поскольку события A, B и С независимы, то, используя теорему умножения вероятностей (1.8), получим

.

Таким образом, поскольку 0,7695>0,7, то предложенный проект следует обсуждать.

В ряде случаев вероятности появления одних событий зависят от того, произошло другое событие или нет. Такие события называются зависимыми. Вероятность события A, вычисленная при условии, что имело место другое событие B, называется условной вероятностью события A и обозначается или .

Вероятность произведения двух событий A и B равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже имело место:

. (1.9)

Пример 1.16. Одна из наиболее сложных проблем рыночных исследований – отказ потребителей отвечать на вопросы о потребительских предпочтениях, либо, если опрос проводится по месту жительства, – отсутствие их дома на момент опроса. Предположим, что исследователь рынка с вероятностью в 0,94 верит, респондент согласится отвечать на вопросы анкеты, если окажется дома. Он также полагает, что вероятность того, что этот человек будет дома, равна 0,65. Имея такие данные, оцените процент заполненных анкет.

Решение. Пусть A – событие того, что респондент окажется дома. Вероятность этого события 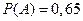. Пусть B – событие того, что респондент согласится отвечать на вопросы. По условию задачи задана условная вероятность 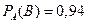, т.е. вероятность того, что он согласится отвечать на вопросы, если он будет дома. Тогда, согласно теореме умножения вероятностей зависимых событий (2.4), вероятность того, что человек будет дома и согласится отвечать на вопросы, будет равна

,

т.е. процент заполненных анкет будет равен 61%.

Вероятность суммы совместных событий A и B равна сумме вероятностей этих событий без вероятности их совместного появления:

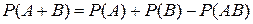. (1.10)

Пример 1.17. Два стрелка делают по одному выстрелу по мишени. Вероятность попадания для первого стрелка равна 0,8, для второго – 0,7. Какова вероятность поражения цели?

Решение. Пусть A ₁={ первый стрелок попал по цели }, A ₂={ второй стрелок попал по цели }. Мишень будет поражена (событие В), если произойдет событие А ₁+ А ₂. Поскольку события А ₁ и А ₂ совместны, но независимы, то

P (А ₁+ А ₂) = P (А ₁)+ P (А ₂)– P (А ₁) P (А ₂) = 0,7+0,8–0,7×0,8 = 0,94.

Отметим, что событие В можно записать также в виде . Тогда получим

P (B) = P (A ₁) P ()+ P ()P(A ₂)+ P (A ₁) P (A ₂) == 0,8×0,3+0,2×0,7+0,7×0,8 = 0,94.

Пример 1.18. Вероятность того, что покупатель, собирающийся приобрести компьютер и пакет прикладных программ, приобретет только компьютер, равна 0,15. Вероятность того, что покупатель купит только пакет программ, равна 0,1. Вероятность того, что будут куплены и компьютер и пакет программ, равна 0,05. Чему равна вероятность того, что будут куплены или компьютер, или пакет программ, или компьютер и пакет программ вместе?

Решение. Пусть A – событие того, что покупатель приобретет компьютер, B – событие того, что покупатель приобретет пакет программ, тогда AB – событие того, что покупатель приобретет и компьютер, и пакет программ. Следовательно, вероятность того, что будут куплены или компьютер, или пакет программ, или компьютер и пакет программ вместе, будет равна

.

Два несовместных события A и называются противоположными, если при эксперименте одно из них обязательно произойдет. Вероятности противоположных событий связаны соотношением

(1.11)

Вероятность появления хотя бы одного из событий A ₁ ,A ₂ ,…, A_n равна разности между единицей и вероятности совместного появления противоположных событий:

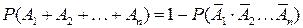. (1.12)

Если события A ₁ ,A ₂ ,…,A_n независимы и их вероятности одинаковы, т.е. и , то

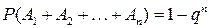. (1.13)

Пример 1.19. Вероятности попадания в цель при стрельбе из трех орудий таковы: p ₁=0,8, p ₂=0,7, p ₃=0,9. Найти вероятность хотя бы одного попадания при одном залпе из всех орудий.

Решение. Поскольку вероятности попаданий независимы и q ₁=1– p ₁=0,2, q ₂=1– p ₂=0,3, q ₃=1– p ₃=0,1, то искомая вероятность равна

P (A) = 1– q ₁ q ₂ q ₃ = 1–0,006 = 0,994.

Пример 1.20. Уличный торговец предлагает прохожим иллюстрированную книгу. Из предыдущего опыта ему известно, что в среднем один из 65 прохожих, которым он предлагает книгу, покупают ее. В течение некоторого промежутка времени он предложил книгу 20 прохожим. Чему равна вероятность того, что он продаст им хотя бы одну книгу?

Решение. Пусть A_i – событие того, что i -й прохожий купит книгу. Вероятность этого события , а противоположного события . Тогда вероятность того, что хотя бы один из 20 прохожих купят книгу, будет равна

.

Если событие A может произойти только с одним из несовместных событий H ₁, H ₂ ,…, H_n, образующих полную группу, т.е. 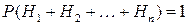, то вероятность события A может быть найдена по формуле полной вероятности:

. (1.14)

Так как заранее неизвестно, какое из событий H ₁, H ₂ ,…, H_n наступит, то их называют гипотезами.

Пример 1.21. В первой урне находится 5 белых и 3 черных шара. Во второй – 4 белых и 5 черных шара. Из первой урны во вторую наугад перекладывают два шара. После этого из второй урны вынимают сразу 4 шара. Какова вероятность того, что шары будут одного цвета?

Решение. По условиям данной задачи, результат второго испытания (т.е. вынимание шаров из второй урны) зависит от того, какие шары были переложены из первой урны. Здесь возможны три случая:

H ₁ = { оба шара белые },

H ₂ = { оба шара черные },

H ₃ = { один белый, один черный шар }.

Очевидно, что события H ₁, H ₂ и H ₃ несовместны и образуют полную группу. Их вероятности равны

, , .

Условные вероятности события А ={ шары одного цвета }, равны

, , .

Применяя формулу полной вероятности, получим

.

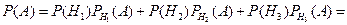
Пример 1.22. Вероятность того, что новый товар будет пользоваться спросом на рынке, если конкурент не выпустит в продажу аналогичный продукт, равна 0,67. Вероятность того, что товар будет пользоваться спросом при наличии на рынке конкурирующего товара, равна 0,42. Вероятность того, что конкурирующая фирма выпустит аналогичный товар на рынок в течение интересующего нас периода, равна 0,35. Чему равна вероятность того, товар будет иметь успех?

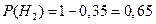Решение. Пусть H ₁ – событие того, что конкурент выпустит в продажу аналогичный продукт, H ₂ – событие того, что конкурент не выпустит в продажу аналогичный продукт. Поскольку эти события несовместные и образуют полную группу, то и . По условию задач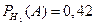и и 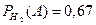, A – событие того, что товар будет иметь успех. В результате по формуле полной вероятности (1.14) находим

.

 

 

Пусть существует несколько предположений (несовместных гипотез) для объяснения некоторого события. Эти предположения проверяются при помощи опыта. Для проведения опыта бывает сложно определить вероятность этих предположений, поэтому им часто приписывают некоторые вероятности, которые называют априорными (доопытными). Затем проводят опыт и получают информацию, на основании которой корректируют априорные вероятности. После проведения эксперимента вероятности гипотез могут измениться. В результате доопытные вероятности заменяются послеопытными (апостериорными).

Переоценку первоначальных гипотез производят по формуле Байеса:

. (1.15)

Пример 1.23. Два автомата производят детали, которые поступают на общий конвейер. Производительность первого автомата вдвое больше производительности второго автомата. Первый автомат производит в среднем 60% деталей отличного качества, а второй – 84% деталей отличного качества. Наудачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что эта деталь изготовлена первым автоматом.

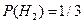Решение. Пусть A – событие того, что деталь изготовлена первым автоматом. Определим гипотезы: H ₁ = {деталь изготовлена первым автоматом}, H ₂ = {деталь изготовлена вторым автоматом}. Поскольку производительность первого автомата вдвое больше производительности второго, то и . По условию задач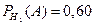и и ,. В результате по формуле полной вероятности (1.14) находим

.

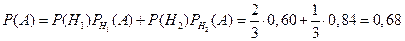В результате, по формуле Байеса находим:

.

Пример 1.24. Экономист-аналитик условно подразделяет экономическую ситуацию в стране на «хорошую», «посредственную» и «плохую» и оценивает вероятности для данного момента времени в 0,15, 0,70 и 0,15 соответственно. Некоторый индекс экономического состояния возрастает с вероятностью 0,7, когда ситуация в стране «хорошая»; с вероятностью 0,4, когда ситуация «посредственная», и с вероятностью 0,1, когда ситуация «плохая». Пусть в настоящий момент времени индекс изменился. Какова вероятность того, что экономика страны на подъёме?

Решение. Пусть событие A – событие того, что «индекс экономического состояния возрастает». Определим гипотезы: H ₁ = {экономическая ситуация в стране на «хорошая»}, H ₂ = {экономическая ситуация в стране на «посредственная»}, H ₃ = {экономическая ситуация в стране на «плохая»}. По условию задач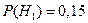и , и 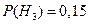, а также , , .

По формуле полной вероятности (1.14) находим

.

В результате, по формуле Байеса находим:

,

т.е. вероятность того, что экономика страны на подъёме равна 0,26.

Формула Бернулли

Испытания Бернулли (или схема повторных испытаний) – это последовательность n независимых испытаний, вероятность появления события А в каждом из которых постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях).

Обозначим вероятность P (A) появлений события А в отдельном испытании буквой p, т.е. P (A)= p. Вероятность противоположного события буквой q, т.е. 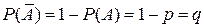. Вероятность P_n (m) того, что в n испытаниях Бернулли событие A появится ровно m раз равна

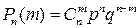. (1.16)

Это есть формула Бернулли.

Пример 1.24. В ходе аудиторской проверки строительной компании аудитор случайным образом отбирает 5 счетов. Если 3% счетов содержат ошибки, чему равна вероятность того, что аудитор: а) найдет только один счет с ошибкой; б) обнаружит не более двух счетов с ошибкой.

Решение. а) Поскольку условия данной задачи удовлетворяют требованиям биномиального распределения, т.е. отбор счетов производится независимо друг от друга, вероятность появления ошибки в каждом счете одна и та же, то для вычисления вероятностей можно воспользоваться формулой Бернулли (1.16), где n =5, p =0,03 и q =1–0,03=0,97. Тогда вероятность того, что аудитор найдет только один счет с ошибкой (m =1), будет равна

.

б) Вероятность того, что аудитор обнаружит не более двух счетов с ошибкой будет равна

Локальная теорема Муавра-Лапласа: если в схеме Бернулли число испытаний n велико, при этом npq ‡1, то справедлива приближенная формула

, (1.17)

где , .

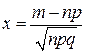Ввиду важности функции j(x), которая называется плотностью стандартного нормального распределения, для нее составлены специальные таблицы (см. приложение 1). При использовании таблиц следует учитывать, что функция j(x) четная, т.е. j(– x)=j(x). Для значений x >4, будем считать, что j(x)=0.

Практика показывает, что аппроксимация (1.17) хорошо проявляется в случае, если np и nq >5, и тем лучше, чем больше n (обычно достаточно n >50). Чем ближе p к 0,5, тем меньше требуется n для более точной аппроксимации.

Пример 1.25. Вероятность того, что сошедшая с конвейера деталь стандартная равна 0,9. Найти вероятность того, что из 400 сошедших с конвейера деталей 356 окажутся стандартными.

Решение. Согласно условию задачи: n =400, m =356, p =0,9, q =0,1. Поскольку n >100 и npq =36>10, то можно применить локальную теорему Муавра-Лапласа. Найдем

.

После этого находим значение функции j(–0,6667)=0,31945. В результате получаем

.

Интегральная теорема Муавра-Лапласа: если в схеме Бернулли число испытаний n велико, то вероятности того, что число успехов заключено в пределах от k ₁ до k ₂, находится по формуле:

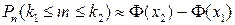, (1.18)

где , – функция Лапласа.

Отметим, что функция Лапласа – нечетная функция, т.е. Ф(– x) = –Ф(x), для которой составлены специальные таблицы (см. приложение 2). Обратите внимание, что 0£Ф(x)£0,5.

Отметим еще, что в некоторых учебниках за функцию Лапласа принимают вдвое большую функцию = 2Ф(x); в этом случае 0£ £1.

Пример 1.26. Вероятность того, что сошедшая с конвейера деталь стандартна равна 0,9. Найти вероятность того, что из 400 сошедших с конвейера деталей более 350 окажутся стандартными.

Решение. Согласно условию задачи: n =400, m =350, p =0,9, q =0,1. Применим теперь интегральную теорему Муавра-Лапласа. В нашем случае k ₁=300, k ₂=400:

, ,

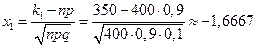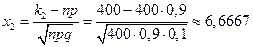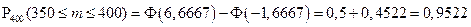
Пример 1.27. Авиакомпания знает, что 5% людей, делающих предварительный заказ на билет определенного рейса, не будут использовать его. Если авиакомпания продала 160 билетов на самолет, в котором лишь 155 мест, чему равна вероятность того, что место будет доступно для любого пассажира, имеющего заказ и планирующего улететь?

Решение. Оценим искомую вероятность при помощи интегральной формулы Муавра-Лапласа, где n =160, k ₁=0, k ₂=155, p =0,95, q =0,05. Тогда

Таким образом, с вероятностью 0,86 место будет доступно для любого пассажира в самолете. Отметим, что более точный результат, подсчитанный при помощи формулы Бернулли, равен 0,91.