Понятие случайной величины является одним из центральных понятий теории вероятностей. Под случайной величиной понимается величина, принимающая в результате испытания то или иное (но при этом только одно) возможное значение, заранее не известное, меняющееся от испытания к испытанию и зависящее от случайных обстоятельств. Случайная величина характеризует все возможные результаты случайного эксперимента с количественной стороны, однако, нельзя достоверно предсказать, какое именно значение при этом она примет.
Случайные величины обозначают обычно большими латинскими буквами, например X, Y, Z, или малыми греческими буквами, например x, z, h, а их возможные значения – малыми латинскими буквами, например x, y, z.
Случайные величины могут быть дискретными и непрерывными. Дискретной случайной величиной (ДСВ) называют такую величину, которая принимает отдельные, изолированные значения с определенными вероятностями. Непрерывной случайной величиной (НСВ) называют такую величину, которая может принимать любое значение из некоторого конечного или бесконечного числового промежутка.
Например, можно считать, что число покупателей в магазине, побывавших там в течение дня, число автомобилей, ремонтируемых еженедельно в данной мастерской, число находящихся в аэропорту являются ДСВ. Курс валют, доход, объем ВНП и т.п. обычно рассматриваются как НСВ.

Для описания случайной величины используется функция распределения – функция F (x), которая определяет вероятность того, что случайная величина X примет значение меньше, чем x, т.е.
 . (2.1)
. (2.1)
На рис. 2.1 изображены характерные графики функций распределения ДСВ (рис. 2.1 а) и НСВ (рис. 2 б).
Из определения функции распределения вытекают следующие ее свойства:
10. Функция распределения F (x) есть неотрицательная функция, заключенная между нулем и единицей:  .
.
20. Функция распределения F (x) есть неубывающая функция, т.е.  .
.
30. Функция распределения F (x) изменяется от 0 до 1 при изменении x от–¥ до +¥:
 ,
,  .
.
40. Вероятность того, что случайная величина примет значение, заключенное в интервале [a,b), равна приращению функции распределения на этом интервале:
 .
.
Для описания ДСВ на практике обычно используется закон распределения (или ряд распределения) вероятностей случайной величины – это когда каждому возможному значению случайной величины ставится в соответствие некоторую вероятность.
Закон распределения обычно записывают в виде таблицы:
| X | x1 | x2 | … | xk |
| P | p 1 | p2 | … | pk |
Обычно  . Обязательно
. Обязательно  .
.
Функция распределения содержит достаточно полную информацию о случайной величине. Действительно, функция распределения одновременно указывает на то, какие значения может принимать случайная величина и с какими вероятностями. Однако судить об основных особенностях случайной величины только по виду функции распределения довольно трудно. Еще труднее сравнивать случайные величины. В связи с этим вводят более простые характеристики случайной величины, определяемые только одним числом. Хотя числовые характеристики не дают полного представления о случайной величине, однако они в сжатой форме выражают наиболее важные черты распределения.
Условно числовые характеристики разделяют на два класса: характеристики положения (математическое ожидание, мода, медиана, начальные моменты) и характеристики рассеивания (дисперсия, среднее квадратичное отклонение, центральные моменты). Важнейшими из них являются математическое ожидание, дисперсия, среднее квадратичное отклонение.
Математическое ожидание характеризует среднее ожидаемое значение случайной величины, т.е. приближенно равно ее среднему значению. Для решения многих задач достаточно знать эту величину. Например, при оценивании покупательской способности населения вполне может хватить знания среднего дохода. При анализе выгодности двух видов деятельности можно ограничится сравнением их средних прибыльностей.
Математическое ожидание ДСВ определяется следующим образом
 . (2.2)
. (2.2)
Из определения математического ожидания вытекают следующие ее свойства:
10.  , где С – постоянная величина.
, где С – постоянная величина.
20.  .
.
30.  .
.
40.  , если X и Y – независимые случайные величины.
, если X и Y – независимые случайные величины.
Дисперсией называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
 , (2.3)
, (2.3)
где  . Раскрыв скобки и используя свойства математического ожидания, получим формулу, которая довольно часто используется для вычисления дисперсии:
. Раскрыв скобки и используя свойства математического ожидания, получим формулу, которая довольно часто используется для вычисления дисперсии:
 , (2.4)
, (2.4)
Из определения дисперсии вытекают следующие ее свойства:
10.  , где С – постоянная величина.
, где С – постоянная величина.
20.  .
.
30.  , если X и Y – независимые случайные величины.
, если X и Y – независимые случайные величины.
Дисперсия имеет размерность, равную квадрату размерности случайной величины, что не всегда удобно при исследовании случайной величины. Для того чтобы представить разброс значений случайной величины в тех же единицах, что и сама случайная величина, вводится числовая характеристика – среднее квадратичное отклонение.
Средним квадратичным отклонением (СКО) называется квадратный корень из дисперсии:
 . (2.5)
. (2.5)
Пример 2.1. Доход от некоторого рискованного бизнеса составляет сумму около 1000 у.е. с заданным законом распределения (знак минус означает убыток):
| X | –2000 | –1000 | ||||
| P | 0,1 | 0,1 | 0,2 | 0,2 | 0,3 | 0,1 |
Какой наиболее вероятностный денежный доход рискованного бизнеса? Является ли этот риск вероятностно-успешным? Определить, чему равен на длительный период средний доход от рассмотренного бизнеса? Какова мера риска вложений в такое предприятие?
Решение. Поскольку сумма всех вероятностей
0,1+0,1+0,2+0,2+0,3+0,1=1,
то представленный ряд действительно является законом распределения вероятностей случайной величины X. Наиболее вероятностный денежный доход этого бизнеса равен 2000, т.к. вероятность этого события P (X =2000)=0,3 наибольшая. Вероятность получить прибыль в этом бизнесе равна P (X >0)=0,2+0,3+0,1=0,6, а вероятность оказаться в убытке равна P (X <0)=0,1+0,1=0,2. Таким образом, риск этого рискованного бизнеса является вероятностно-успешным.
Средний доход от рассмотренного бизнеса за длительный период равен математическому ожиданию:
 у.е.
у.е.
Мерой риска вложений в рискованное предприятие может служить среднее квадратичное отклонение. Вычислим дисперсию по формуле (2.4), предварительно найдем
 .
.
Тогда
 .
.
Следовательно, СКО будет равна
 у.е.
у.е.
Таким образом, разброс значений случайной величины достаточно большой, следовательно, рассматриваемый бизнес имеет очень высокий уровень риска.
Пример 2.2. Дискретная случайная величина Х имеет только два возможных значения: x 1 и x 2, причем x 1 < x 2. Вероятность того, что Х примет значение x 1 равно 0,6. Найти закон распределения Х, зная математическое ожидание М[ X ] = 1,4 и дисперсию D[ X ] = 0,24.
Решение. Сумма вероятностей всех возможных значений X равна единице, поэтому вероятность того p 2, что X примет значение x 2, равна 1–0,6=0,4. Запишем закон распределения дискретной случайной величины X:
| X | x 1 | x 2 |
| P | 0,6 | 0,4 |
Для отыскания x 1 и x 2 составим два уравнения. По определению
 ,
,  .
.
Учитывая, что по условию М[ X ] = 1,4, запишем первое из уравнений:
 .
.
Принимая во внимание, что по условию D[ X ] = 0,24, напишем второе уравнение:
 , или
, или  .
.
В результате получается следующая система уравнений:

Выразив x 1 из первого уравнения и подставив его во второе, получим квадратное уравнение
 .
.
Отсюда находим два решения:  и
и 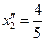 , соответственно,
, соответственно,  и
и  . По условию
. По условию  , поэтому задаче удовлетворяет только первое решение. Таким образом, искомый закон распределения имеет вид
, поэтому задаче удовлетворяет только первое решение. Таким образом, искомый закон распределения имеет вид
| X | ||
| P | 0,6 | 0,4 |