Для оптимальности допустимого вектора х= (х1,х2…,хn,) в задаче 1 достаточно существование m-мерного вектора у =(у1,у2,у3,…,уm), удовлетворяющего условиям:
а) уi і 0, iОI2
б) еaijyi + cj = 0, jОJ1,
iОI
в) еaijyi + cj, £ 0, jОJ2,
iОI
г) еaijyi + cj, = 0, если хj >0 для jОJ2,
iОI
д) уi = 0, если еaijxj + bi >0, iОI2,
jОJ
тогда вектор у является оптимальным в задаче 1*.
Пример применения признака оптимальности в развернутой форме
Как этим признаком пользоваться?
Предположим, что мы имеем допустимый вектор х, т.е. хj ≥0 и такие, что 
, 
.
Тогда попытаемся найти вектор у из уравнений б), г), д). Эта система совместна и имеет единственное решение, если выполняются следующие условия:
1) Количество уравнений в системе m (совпадает с числом переменных);
2) Матрицы при неизвестных – неособенные
Пример применения признака оптимальности в развернутой форме
Проверить вектор 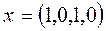 на оптимальность в следующей задаче ЛП:
Максимизировать
при условиях:
| Решение. Решение задачи необходимо начинать с проверки допустимости данного вектора  .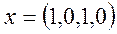
Подставляя значения компонент вектора в ограничении I0 и 20, убеждаемся, что все они выполняются. Для проверки остальных условий признака оптимальности составляем двойственную задачу:
Требуется найти вектор  , удовлетворяющий условиям:
|
Пример применения признака оптимальности в развернутой форме
Проверить вектор 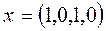на оптимальность в следующей задаче ЛП:
Максимизировать
при условиях:
| еaijyi + cj, = 0, если хj >0 для jОJ2,
i  I – условие г)
Запишем условие г) признака оптимальности:
(т.к.  , следовательно, в первом и третьем ограничении условия 20 двойственной задачи достигается равенство)
|
Пример применения признака оптимальности в развернутой форме
| Проверить вектор 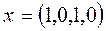на оптимальность в следующей задаче ЛП:
Максимизировать
при условиях:
| д) отсутствует, т.к. ни одно ограничение 20 основной задачи не выполняется как строгое неравенство.
Из условия г) находим  .
Найден вектор  . Проверяем его допустимость в двойственной задаче, т.е. выясняем, выполняются ли условия I0 и 20 двойственной задачи. Т.к. все условия выполняются, вектор y является оптимальным в двойственной задаче, а вектор х =(1, 0, 1, 0)- оптимальным в основной задаче.
|
Основная теорема теории линейного программирования
И ее следствия
Для разрешимости задачи математического программирования (как и в любой оптимизационной задачи) необходимо, чтобы множество допустимых решений было не пусто, и целевая функция на этом множестве была ограничена сверху (если задача на максимум), либо снизу (если задача на минимум).
Теорема двойственности. Каковы бы ни были исходные данные, для задач 1 и 1* имеет место один из следующих взаимоисключающих случаев.
1. В задачах 1 и 1* имеются оптимальные векторы х и у и 
, т.е. обе задачи разрешимы.
2. В задаче 1 существуют допустимые векторы х из некоторого множества Х, но линейная функция 
на множестве этих векторов не ограничена сверху, т.е. 
, тогда в задаче 1* нет допустимых векторов.
3. В задаче 1* существуют допустимые векторы 
, но функция 
не ограничена снизу на множестве этих векторов, т.е. 
, тогда в задаче 1 нет допустимых векторов.
4. В задачах 1 и 1* нет допустимых векторов, то есть 