История математического программирования

 

Велись разработки ПО для реализации симплекс – метода для решения задачи ЛП (И.В. Романовский, А.А. Станевичус, и др, доцент УГАТУ А.П. Мартынов).

Появились численные методы решения специальных классов задач ЛП:

транспортная задача, методы декомпозиции, итеративные методы ЛП.

Практическое применение ЛП для социалистической экономики.

9. 70-80-е годы

Вводится новое понятие сложности оптимизационной задачи: установлены нижние границы для различных классов оптимизационных задач (Юдин Д.Б. и др.).

Было установлено: если метод имеет сложность, совпадающую с нижней границей, то он оптимален, т.е. не существует методов, которые решают все задачи класса быстрее (в отношении порядка).

Построен итеративный метод решения задачи ЛП, для которой была доказана полиномиальная сходимость (Хачиян Л.Г.)

 

Литература

1.Канторович Л.В. Математические методы организации и планирования производства. Л.: Изд-во Ленинградский университет, 1939, 64с.

2. Юдин Д.Б., Гольштейн Е.Г. Задачи и методы линейного программирования. М.: Советское радио. 1964, 491с.

3. Карманов В.Г. Математическое программирование. М.: Наука, 1975, 272с.

4. Мухачева Э.А., Рубинштейн Г.Ш. Математическое программирование. Новосибирск: Изд-во «Наука», Сибирское отделение, 1987, 272с.

5. Мухачева Э.А. Рациональный раскрой промышленных материалов. Применение АСУ. М.: Машиностроение, 1984,174с.

6. Мухачева Э.А., Верхотуров М.А., Мартынов В.В. Модели и методы расчета раскроя-упаковки геометрических объектов. Уфа: УГАТУ, 1998, 217с.

7. Мухачева Э.А., Валеева А.Ф., Картак В.М. Задачи двухмерной упаковки в контейнеры: новые подходы к разработке методов локального поиска оптимума. Москва: Изд-во МАИ, 2004, 192с.

Главные научные центры по математическому программированию

 

Москва: МГУ, Центральный экономико-математический институт, Вычислительный центр

 

Киев: Институт кибернетики им. В.М. Глушкова

 

Новосибирск: Институт математики им. С.Л. Соболева Сибирского отделения РАН, Новосибирский государственный университет

 

Ленинград: Ленинградский государственный университет

 

Задача планирования производства

Вид сырья Нормы расхода сырья (кг) на одно изделие Общее количество сырья на складе (кг) А В I II III       Прибыль от реализации одного изделия (у.е.)

Учитывая, что изделия А и В могут производиться в любых соотношениях (сбыт обеспечен), требуется составить такой план их выпуска, при котором прибыль предприятия от реализации всех изделий будет максимальной. Предположим, что предприятие изготовит х1 изделий вида А и х2 изделий вида В. Поскольку производство продукции ограничено имеющимся в распоряжении предприятия сырьем каждого вида, и количество изготовленных изделий не может быть отрицательным, должны выполняться следующие условия: 1) х1, х2 ³ 0 2) 12х1 + 4 х2 £ 300 4 х1 + 4 х2 £ 120 3 х1 + 12 х2 £ 252 Максимальная прибыль от реализации х1 изделий вида А и х2 изделий вида В составит m(х) = max (30 х1 + 40 х2 ) x

Задача об оптимальной смеси

Цель – подобрать оптимальный состав коктейля из трех компонентов: коньяка, шампанского и сока. Стоимости ингредиентов смеси соответственно: с1=50, с2=100, с3=20; Содержание в них алкоголя: а1=0,4; а2=0,5; а3=0,0; Вкусовые качества в баллах: в1=4, в2=8, в3=10.

Пусть хi(i = 1,2,3) – доля каждого компонента в коктейле (все расчеты ведем на единицу объема). Стоимость коктейля определится функцией: f1(x1, x2, x3)= с1 x1+ с2 x2+ с3 x3 Крепость коктейля определится функцией: f2(x1, x2, x3)= a1 x1+ a2 x2+ a3 x3 Вкус коктейля определится функцией: f3(x1, x2, x3)= в1 x1+ в2 x2+ в3 x3 Естественное желание – получить коктейль минимальной стоимости, максимальной крепости и максимального вкуса (противоречивые критерии!)

Задача об оптимальной смеси (продолжение)

 

Выберем критерий – оптимизация стоимости, а остальные критерии ограничим на требуемом уровне:

Крепость ограничим долей алкоголя в 0,2, а вкус – 8 баллами.

 

При этом должны выполняться следующие условия:

1) х_i ≥ 0 (i = 1,2,3)

2) 0,4 x₁+ 0,5 x₂+ 0 x₃ ≥ 0,2

4 x₁+ 8 x₂+ 10 x₃ ≥ 8

x₁+ x₂+ x₃ =1

Минимальная стоимость составит

 

m(х) =min (50 x₁+ 100 x₂+ 20 x₃)

x

 

 

Некоторые определения

Выпуклой комбинацией n точек x₁, x₂,…,x_n называется любая линейная комбинация вида λ₁x₁+λ₂x₂+…+λ_nx_n=x, где λ_j≥0, λ₁+λ₂+…+λ_n=1, j=1,2,…,n.

Некоторые определения

 

Некоторые определения

1. Пусть М = {a₁, a₂,..., а_m} – множество вещественных чисел R

Подмножество М на­зывают ограниченным сверху, если все его элементы не пре­восходят некоторого с R, где с называют верхней границей для М.

 

2. Для каждого ограниченного сверху непу­стого множества M 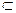R среди его верхних границ имеется минимальная, которую называют супремумом множества М и обозначают через sup M. Если же множество M 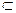R не является ограниченным сверху, то пишут sup M=+ .

Множество М 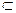R называют ограниченным снизу, если все его элементы не меньше некоторого числа с R.

Соответствующие с R называют нижними грани­цами, а наибольшую из них — инфимумом множества М, который обозначают через inf M.

Если же множество M 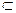R не является ограниченным снизу, то пишут

inf M =- .

Некоторые определения

3. Не каждое ограниченное сверху множество M 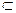R имеет наибольший элемент, обозначаемый обычно через max М. Однако если такой элемент существует, то max М = sup М.

Если в множестве M 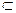R име­ется наименьший элемент, обозначаемый через min M, то это множество является ограниченным снизу и при этом min М= inf M.

 

5. Система векторов x₁, x₂,…,x_r, r≥2, называется линейно зависимой, если хотя бы один из векторов системы является линейной комбинацией остальных, и линейно независимой – в противном случае.

 

6. Максимальное число линейно независимых векторов в n-мерном пространстве равно n.

 

7. Любая совокупность n линейно независимых векторов n-мерного пространства образует базис n-мерного пространства.

 

 

Некоторые определения

8. Какова бы ни была прямоугольная матрица

,

 

максимальное число линейно независимых строк (т. е. со­ответствующих n-мерных векторов) совпадает с максималь­ным числом линейно независимых столбцов (т. е. соответ­ствующих m-мерных векторов). Это число называется ран­гом матрицы А. При этом квадратную матрицу

порядка m называют неособенной, если ее ранг r совпадает с m. Если отвечающая системе линейных уравнений квадратная матрица А является неособенной, то эта система имеет единственное решение при любых свободных членах .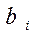

Некоторые определения

 

Задачи выпуклого программирования: целевая функция f и все функции

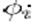(а следовательно, и множество допустимых решений Q) являются выпуклыми; любой локальный минимум является глобальным.

Задачи линейного программирования: все функции f и

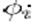являются линейными, так что множество допустимых решений Q оказывается выпуклым линейным многогранным множеством.

Рассмотренные задачи (слайды 8-10) - являются задачами линейного программирования (ЛП).

 

Любой вектор Х, удовлетворяющий ограничениям задачи ЛП, называется допустимым вектором.

 

Допустимый вектор, доставляющий max или min целевой функции задачи ЛП, называется оптимальным вектором.