Итак, базисное множество является двойственно допустимым, если величины
, 
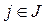, (18)
удовлетворяют неравенствам
, 
(19)
Отметим, что величины (18) тесно связаны с коэффициентами разложения соответствующих векторов 
по рассматриваемым базисным векторам, а именно:
, 
, (20)
где 
- коэффициенты разложения векторов 
по рассматриваемому базису, т. е. 
. (21)
Действительно, учитывая (18), (21),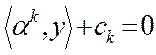 
, 
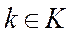и свойства скалярного произведения, получаем
. (22)
Лемма 2
Каково бы ни было базисное множество K, для соответствующих векторов х (К) и у (К) имеет место равенство
.
Доказательство. Так как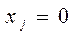 
, 
, 
, 
, 
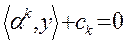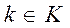получаем
,
что и требовалось показать.▄
Следствие из леммы 2 и признака оптимальности
Задача А. Максимизировать линейную функцию
 на множестве n -мерных векторов
х = (х1, х2,..., хn),
удовлетворяющих условиям
1.  ,  ,
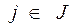2. 
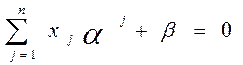
| Задача А*.Минимизировать линейную функцию
на множестве m-мерных векторов
y = (y1, y2,..., ym),
удовлетворяющих системе линейных неравенств
1. -
2.  ,  .
|
Теорема. Если базисное множество К является одновременно допустимым и двойственно допустимым базисным множеством, то отвечающие ему векторы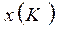 
и 
оптимальные соответственно в задачах А и А*.
Доказательство. Пусть К – допустимое базисное множество и двойственно допустимое базисное множество. Это значит, что вектора 
и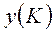 
- допустимые. На основании леммы 2 
, а это достаточно для того, чтобы вектор 
был оптимальным и вместе с ним и вектор 
(см. краткую форму достаточного признака оптимальности)▄
Лемма 3
Пусть задано некоторое базисное множество К и отвечающий ему вектор
х (К) = (х1, х2,..., хп). Кроме того, для некоторого 
известны коэффициенты gk в разложении вектора 
посоответствующим базисным векторам:
= 
.
Тогда при любом 
вектор 
= (
) с компонентами
, 
, 
, 
, 
,
удовлетворяет условию 
, причем значение линейной функции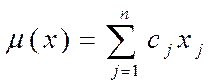 
на этом векторе может быть вычислено по формуле
,где величина 
определяется из системы 
, 
.
Лемма 3
Доказательство. Имеем: = (23)
После умножения соотношения (18) на и переноса всех его членов в левую часть получаем равенство: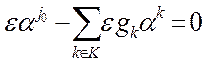 
(24)
Имеем: (25)
Складывая (19) и (20), получаем
. (26)
Следовательно, интересующий нас вектор 
удовлетворяет требуемому условию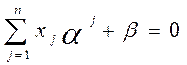 
. Далее, для вектора 
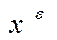выполнены равенства (в силу того, что 
, 
, , 
, 
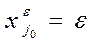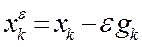и (22))
(27) ▄
Следствие 1 из леммы 3
Вектор должен удовлетворять условию неотрицательности, т.е.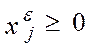 
.
Возможны два случая:
а). Все коэффициенты gk≤ 0 в
б) среди коэффициентов gk имеются положительные
Следствие 1. Если имеет место случай а),то векторы 
, определяемые в лемме 3, являются допустимыми в задаче А при всех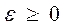 
, а линейная функция 
на множестве таких векторов не ограничена сверху.
Действительно,
По теореме двойственности (слайд 42) в двойственной задаче допустимый вектор не существует, следовательно, вектор х не оптимальный ▄
Следствие 2 из леммы 3
Вектор должен удовлетворять условию неотрицательности, т.е. .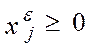
Случай б) среди коэффициентов gk имеются положительные
Следствие 2. Если имеет место случай б),то векторы 
являются допустимыми в задаче А лишь при 
, где
,
причем
.
Пусть 
; 
выполняется всегда; 
. Тогда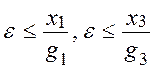 
, чтобы эти неравенства выполнялись одновременно, находят 