Задача (2)-(4) получена на основе физических законов, ответственных за процесс переноса нейтронов. Дальнейший анализ задачи невозможен без ее математической корректной постановки. Для этого требуется не только формальная запись соответствующего интегродифференциального уравнения и дополнительных (граничных и начальных) условий, но и указание класса функций, в котором ищется решение. Упомянутый класс функций должен быть согласован с физическим смыслом рассматриваемого процесса и таким, чтобы входящие в уравнение операторы имели смысл. Поэтому естественно начать рассмотрение с ограничений, накладываемых на функции ядерно-физических характеристик среды:
Свойства этих функций оказывают существенное влияние на структуру области определения уравнения (2) и являются по отношению к нему исходными данными.
Прежде всего отметим, что всякая ядерно-физическая установка, основанная на принципе процессов ядерного деления нейтронами, состоит из конечного числа областей (зон), однородных относительно ядерно-физических характеристик среды. Допустим, что однородные зоны разделены гладкими поверхностями. Отсюда следует, что ядерные плотности изотопов 
неотрицательны в области 
, кусочно-непрерывные (возможно непрерывные) функции пространственной переменной 
Кроме того, по своему смыслу функции ограничены сверху; поскольку их конечное число, то
(5)
иными словами, ядерные плотности всех изотопов среды равномерно ограничены. Сомнения могут вызвать лишь точки 
, лежащие на границах раздела зон (если таковые существуют) - в этих точках функции не определены. Для преодоления этого технического затруднения будем считать, не ограничивая общности рассуждений, что поверхности раздела однородных зон, как и граница 
области , имеют лебегову меру нуль; иными словами, будем считать, что функции определены почти всюду в области относительно меры Лебега на . Тогда условие (5) следует заменить равномерной ограниченностью по существенному максимуму:
(6)
здесь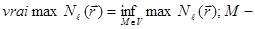 
произвольное множество из области меры нуль.
Далее будем предполагать, что в области нет областей с отличной от нуля мерой, не заполненных веществом; иными словами, нет вакуумных пустот. Этот факт означает, что полная ядерная плотность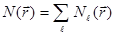 
отлична от нуля почти всюду в области , за исключением границы раздела однородных зон, где функция 
не определена. Поэтому можно записать:
(7)
Отсюда с учетом (7) находим
(8)
Несколько сложнее обстоит дело с функциями распределения вторичных нейтронов 
. Оценка газовой модели вещества показывает, что функции распределения вторичных нейтронов, отвечающие упругому рассеянию, могут иметь особенность при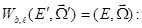 
(9)
здесь 
- непрерывная в области изменения своих аргументов функция на 
множество ортов 
. Поскольку множество 
замкнуто, то из непрерывности функций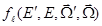 
следует их равномерная ограниченность.
Все остальные функции 
особенностей не имеют и могут быть представлены в виде
(10)
здесь 
непрерывные и равномерно ограниченные на функции.
Везде далее изложенные выше требования будем считать выполненными.