Введем новую переменную 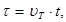 где
где 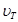 - некоторая характерная скорость нейтрона (например, наиболее вероятная скорость в максвелловском распределении нейтронного газа по скоростям с температурой T;
- некоторая характерная скорость нейтрона (например, наиболее вероятная скорость в максвелловском распределении нейтронного газа по скоростям с температурой T;  , m-масса нейтрона) и выразим кинетическую энергию в безразмерных единицах
, m-масса нейтрона) и выразим кинетическую энергию в безразмерных единицах

Тогда уравнение (2) можно записать в удобном для дальнейшего анализа виде:
 (11)
(11)
здесь: 
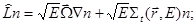

с начальным

и граничным
 (12)
(12)
условиями. В уравнении (11), в отличие от уравнения (2), интеграл по всей энергетической оси заменен интегралом по конечному промежутку  Такая замена произведена с целью упрощения анализа и не противоречит физическому смыслу энергетической переменной. Действительно, в спектре ядерного реактора почти полностью отсутствуют нейтроны с энергией E > 10 Mэв. Поэтому естественно принять, что энергия нейтронов ограничена сверху.
Такая замена произведена с целью упрощения анализа и не противоречит физическому смыслу энергетической переменной. Действительно, в спектре ядерного реактора почти полностью отсутствуют нейтроны с энергией E > 10 Mэв. Поэтому естественно принять, что энергия нейтронов ограничена сверху.
Перейдем к описанию рабочего пространства функций нашей задачи, что не является тривиальной задачей. С другой стороны, удачный выбор функционального пространства во многом предопределяет успех последующего анализа. Естественно, на первом этапе большую роль играет понимание физики процесса и априорная информация о гладкости процессов, входящих в уравнение. Дальнейшее уточнение структуры рабочего пространства функций производится в процессе анализа задачи с целью детализации свойств ее решения.
Поскольку ядерные плотности  не определены на поверхностях раздела однородных зон (если таковые имеются) и на поверхности
не определены на поверхностях раздела однородных зон (если таковые имеются) и на поверхности 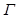 области
области 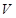 , таким же свойством должны обладать функции
, таким же свойством должны обладать функции  , среди которых мы ищем решение задачи (11)-(12).
, среди которых мы ищем решение задачи (11)-(12).
Не ограничивая общности рассмотрения, будем считать, что меры выше упомянутых областей равны нулю относительно меры области 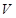 ; случай, когда меры поверхностей раздела зон отличны от нуля, не представляет интереса, поскольку он нереализуем на практике.
; случай, когда меры поверхностей раздела зон отличны от нуля, не представляет интереса, поскольку он нереализуем на практике.
Итак, допустимые функции  при каждом
при каждом  определены почти всюду в области
определены почти всюду в области
 (13)
(13)
имеющей конечную меру, равную произведению мер области 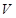 промежутка
промежутка  и множества направлений
и множества направлений  . При этом
. При этом  где
где  - лебегова мера области
- лебегова мера области  .
.
Итак, в допустимом множестве должны содержаться функции, удовлетворяющие граничному условию (12) и функции такие, что на них имеет смысл оператор 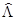 .
.
При построении рабочего пространства переменная  играет роль параметра, однако зависимость от
играет роль параметра, однако зависимость от  должна допускать существование
должна допускать существование 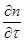 при
при  и, согласно уравнению (11), принадлежность этой производной области
и, согласно уравнению (11), принадлежность этой производной области 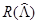 оператора
оператора 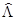 .
.
Множество функций, удовлетворяющих вышеуказанным требованиям относительно переменных  , содержится в хорошо известных лебеговых пространствах
, содержится в хорошо известных лебеговых пространствах  где
где  - область изменения переменных
- область изменения переменных  , определяемая равенством (13); индекс
, определяемая равенством (13); индекс  представляет собой степень, с которой суммируется модуль функции по области
представляет собой степень, с которой суммируется модуль функции по области  . Напомним, что в
. Напомним, что в  функции, равные почти всюду относительно меры в области
функции, равные почти всюду относительно меры в области  , считаются эквивалентными. С учетом этого множества пространств
, считаются эквивалентными. С учетом этого множества пространств  при
при  представляют собой линейное пространство над полем комплексных чисел. Эти пространства полны относительно норм
представляют собой линейное пространство над полем комплексных чисел. Эти пространства полны относительно норм

 ,
,
то есть являются комплексными банаховыми пространствами.
Теперь можно определить рабочее пространство  для рассматриваемой задачи как множество функций
для рассматриваемой задачи как множество функций  действительной переменной
действительной переменной  со значениями в банаховом пространстве
со значениями в банаховом пространстве  ,
,  . Наличие нормы в пространстве
. Наличие нормы в пространстве  позволяет естественным образом ввести понятие непрерывности
позволяет естественным образом ввести понятие непрерывности 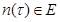 и определить производную
и определить производную 
Определение 1. Функция 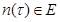 называется непрерывной в точке
называется непрерывной в точке  , если
, если
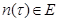

где предельный переход осуществляется в одном из пространств  ,
,  .
.
Функция 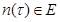 непрерывна на промежутке [0,T], если она непрерывна в каждой его точке (непрерывность в точке нуль понимается как непрерывность справа).
непрерывна на промежутке [0,T], если она непрерывна в каждой его точке (непрерывность в точке нуль понимается как непрерывность справа).
Определение 2. Если существует элемент  такой, что
такой, что
 (14)
(14)
то 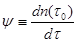 называется производной функции
называется производной функции 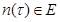 в точке
в точке 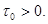 В случае
В случае  предел в (14) находится справа. Нетрудно видеть, что если
предел в (14) находится справа. Нетрудно видеть, что если 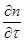 сушествует в каждой точке промежутка [0,T], то она сама является функцией со значениями в пространстве
сушествует в каждой точке промежутка [0,T], то она сама является функцией со значениями в пространстве  . Кроме того, функция
. Кроме того, функция 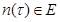 , имеющая в
, имеющая в 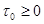 производную, непрерывна в этой точке.
производную, непрерывна в этой точке.
Включим в область определения  оператора
оператора 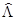 лишь те функции из
лишь те функции из  ,
,  , которые удовлетворяют граничному условию. Пусть в каждом из пространств
, которые удовлетворяют граничному условию. Пусть в каждом из пространств  подмножество
подмножество 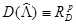 . Тогда рассматриваемая задача состоит в отыскании решения уравнения
. Тогда рассматриваемая задача состоит в отыскании решения уравнения
 (15)
(15)
с начальным условием
 (16)
(16)
здесь  и
и  - функции из E со значениями в одном из подходящих пространств
- функции из E со значениями в одном из подходящих пространств  ,
, 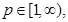 причем
причем  при каждом
при каждом 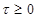 ; напомним, что функции из
; напомним, что функции из  удовлетворяют граничному условию.
удовлетворяют граничному условию.
Для завершения постановки задачи необходимо определить понятие решения уравнения (15) с начальным условием (16).
Определение 3. Функция  со значениями в подпространстве
со значениями в подпространстве 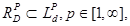 называется решением задачи (15)-(16) на интервале
называется решением задачи (15)-(16) на интервале  если:
если:
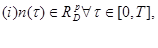
(ii) в каждой точке  существует производная
существует производная 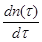 ;
;
(iii) уравнение (15) удовлетворяется для всех  ;
;
(iv)  .
.
Уравнение (15) принято называть эволюционным, задачу (15)-(16) – задачей Коши:
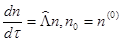 , (17)
, (17)
поскольку свойства решений неоднородной задачи (15)-(16) прямо следуют из свойств решений АЗК (17).