Выше нестационарная задача переноса нейтронов без учета запаздывающих нейтронов была сформулирована как АЗК в банаховых пространствах  . Далее необходимо установить, какими свойствами должны обладать оператор
. Далее необходимо установить, какими свойствами должны обладать оператор  и область
и область  определения, чтобы решение АЗК существовало. Этим вопросам посвящена теория полугрупп операторов; ниже кратко будут изложены основные результаты этой теории применительно к АЗК (17). Установление перечня достаточных условий существования решений АЗК в банаховом пространстве одновременно представляет собой схему дальнейшего анализа АЗК (17).
определения, чтобы решение АЗК существовало. Этим вопросам посвящена теория полугрупп операторов; ниже кратко будут изложены основные результаты этой теории применительно к АЗК (17). Установление перечня достаточных условий существования решений АЗК в банаховом пространстве одновременно представляет собой схему дальнейшего анализа АЗК (17).
Отметим, что частным случаем задачи (17) является задача Коши для обыкновенного дифференциального уравнения

где  - числовой коэффициент, которое имеет решение
- числовой коэффициент, которое имеет решение
 (18)
(18)
По аналогии с (18) запишем формальное решение АЗК (17) в виде
 (19)
(19)
В связи с записью (19) естественно возникает ряд вопросов, первым и наиболее важным из которых является следующий: как можно определить экспоненциальную функцию от оператора  .
.
Определение 4. Семейство операторов  называется полугруппой, если
называется полугруппой, если
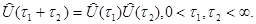 (20)
(20)
Если сохранить за операторной функцией  основное свойство экспоненты:
основное свойство экспоненты:

то согласно определению 4 семейство 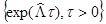 является полугруппой операторов и задача обоснования выражения (19) состоит в нахождении условий существования полугруппы
является полугруппой операторов и задача обоснования выражения (19) состоит в нахождении условий существования полугруппы  . Эта задача решается просто, если оператор
. Эта задача решается просто, если оператор  ограничен. Действительно, пусть
ограничен. Действительно, пусть 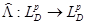 - ограниченный оператор и
- ограниченный оператор и  при каком-либо
при каком-либо  . Тогда ряд
. Тогда ряд
 (21)
(21)
абсолютно сходится для любого комплексного  , то есть сходится ряд
, то есть сходится ряд  следовательно, этот ряд является при каждом
следовательно, этот ряд является при каждом  ограниченным оператором в
ограниченным оператором в  и аналитической функцией параметра
и аналитической функцией параметра  со значениями в пространстве ограниченных операторов.
со значениями в пространстве ограниченных операторов.
Проверка полугруппового свойства (20) для ряда (21) формально проводится также, как и в числовом случае. В силу аналитичности по  ряд (21) можно дифференцировать формально опять также, как в числовом случае. В результате находим
ряд (21) можно дифференцировать формально опять также, как в числовом случае. В результате находим
 (22)
(22)
где производная понимается в смысле определения 2, но по норме в пространстве ограниченных операторов. Из соотношения (22) немедленно следует, что
 (23)
(23)
для произвольного элемента  . Если принять
. Если принять
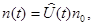 (24)
(24)
то запись (23) будет означать, что функция (24) является решением АЗК (17) в случае ограниченного оператора  при начальном условии
при начальном условии  .
.
Таким образом, в случае ограниченного оператора  решение АЗК (17) действительно определяется выражением (19) для произвольного элемента
решение АЗК (17) действительно определяется выражением (19) для произвольного элемента  , если положить
, если положить
 ;
;
иными словами, решение выражается с помощью оператора полугруппы  согласно выражения (21). Однако оператор
согласно выражения (21). Однако оператор  в действительности не ограничен в
в действительности не ограничен в  , что будет строго доказано ниже. Тем не менее, уже на данном этапе анализа наличие в операторе
, что будет строго доказано ниже. Тем не менее, уже на данном этапе анализа наличие в операторе  производных по пространственным переменным позволяет допустить его неограниченность.
производных по пространственным переменным позволяет допустить его неограниченность.
В этом случае обоснование решения вида (18) налагает на оператор  достаточно сильные ограничения и проводится значительно сложнее. Идея остается прежней: необходимо корректно определить полугруппу (экспоненциальную функцию) операторов и убедиться в справедливости соотношения (23) уже не для произвольного элемента
достаточно сильные ограничения и проводится значительно сложнее. Идея остается прежней: необходимо корректно определить полугруппу (экспоненциальную функцию) операторов и убедиться в справедливости соотношения (23) уже не для произвольного элемента  , а для
, а для 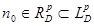 .
.
Совершенно очевидно, что ряд (21) определения полугруппы не пригоден для неограниченного оператора  , поскольку области определения операторов
, поскольку области определения операторов  сужаются с ростом
сужаются с ростом 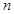 . По аналогии с числовым случаем можно пытаться использовать разложение
. По аналогии с числовым случаем можно пытаться использовать разложение
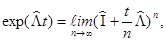
где предел понимается в смысле операторной нормы. Однако такое определение некорректно по той же причине, что и определение полугруппы согласно (21). Тем не менее, аналогия с числовым случаем и здесь оказывается эффективной - незначительное изменение последнего выражения, а именно
 (25)
(25)
уже оказывается полезным. Действительно, при определенных условиях оператор  является с точностью до постоянной резольвентой оператора
является с точностью до постоянной резольвентой оператора  , которая является голоморфной функцией в резольвентном множестве со значениями в пространстве ограниченных операторов в
, которая является голоморфной функцией в резольвентном множестве со значениями в пространстве ограниченных операторов в  . Для того чтобы резольвента
. Для того чтобы резольвента  представляла собой непрерывный линейный оператор, определенный во всем пространстве
представляла собой непрерывный линейный оператор, определенный во всем пространстве  , достаточно замкнутости оператора
, достаточно замкнутости оператора  .
.
Будем считать далее: (А) Оператор  замкнут; (В) Положительная вещественная полуось принадлежит резольвентному множеству оператора
замкнут; (В) Положительная вещественная полуось принадлежит резольвентному множеству оператора  и резольвента
и резольвента  удовлетворяет неравенству
удовлетворяет неравенству


Отсюда следует оценка

 (26)
(26)
Поэтому операторнозначные функции
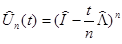 (27)
(27)
равномерно ограничены ( и голоморфны по
и голоморфны по 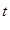
 >0. Кроме того, из свойств резольвенты вытекает, что функция
>0. Кроме того, из свойств резольвенты вытекает, что функция  сильно сходится к
сильно сходится к  при
при  то есть
то есть  для любого элемента
для любого элемента  . Далее, чтобы убедиться в справедливости соотношения (25) в предположениях (А) и (В), необходимо, как и в простом числовом случае, установить существование предела последовательности
. Далее, чтобы убедиться в справедливости соотношения (25) в предположениях (А) и (В), необходимо, как и в простом числовом случае, установить существование предела последовательности  при
при  и убедиться, что этот предел представляет собой полугруппу. Это можно установить при дополнительном условии (А1): область определения
и убедиться, что этот предел представляет собой полугруппу. Это можно установить при дополнительном условии (А1): область определения  оператора
оператора  плотна в пространстве
плотна в пространстве  . Доказательство мы опускаем (см., например, [1]), поскольку оно связано с тонкими деталями, не относящимися к существу вопроса.
. Доказательство мы опускаем (см., например, [1]), поскольку оно связано с тонкими деталями, не относящимися к существу вопроса.
Итак, функция
 , (28)
, (28)
где подразумевается сильная сходимость, является полугруппой операторов со свойствами:
1. 
2. 
3.  сильно непрерывна то есть функция
сильно непрерывна то есть функция  непрерывна по
непрерывна по 

в смысле нормы в  при любом
при любом 
4. 
Здесь первое свойство есть просто определение полугруппы; второе свойство немедленно следует из (26) и существования предела (28); третье свойство также следует из факта сильной сходимости последовательности операторов (27), однако оно не столь очевидно, как первые два и требует аккуратного доказательства, которое мы предлагаем провести в качестве полезного упражнения читателю. Четвертое свойство, как и в случае ограниченного оператора (см. (23)), означает, что функция  является решением АЗК (17) с неограниченным оператором
является решением АЗК (17) с неограниченным оператором  , удовлетворяющим условиям (А) и (А1). Доказательство четвертого свойства мы также опускаем ввиду его трудоемкости (см., например, [1]).
, удовлетворяющим условиям (А) и (А1). Доказательство четвертого свойства мы также опускаем ввиду его трудоемкости (см., например, [1]).
Оператор  называется производящим (инфинитезимальным) оператором полугруппы
называется производящим (инфинитезимальным) оператором полугруппы  . Важно отметить, что полугруппа, порождаемая оператором
. Важно отметить, что полугруппа, порождаемая оператором  в условиях (А), (А1), (В), единственна. Другими словами, решение АЗК (17), определяемое выражением
в условиях (А), (А1), (В), единственна. Другими словами, решение АЗК (17), определяемое выражением  единственно.
единственно.
Для установления этого утверждения достаточно убедиться в справедливости выражения
 (29)
(29)
которое устанавливает связь между резольвентой  оператора
оператора  и порождаемой им полугруппы
и порождаемой им полугруппы  . Интеграл в (29) следует понимать как несобственный интеграл Римана, то есть как сильный предел интегралов
. Интеграл в (29) следует понимать как несобственный интеграл Римана, то есть как сильный предел интегралов 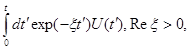 при
при  Последний интеграл имеет смысл в силу непрерывности подинтегральной функции по
Последний интеграл имеет смысл в силу непрерывности подинтегральной функции по  (в силу свойства 3 полугруппы
(в силу свойства 3 полугруппы  ). Предел
). Предел

cуществует, поскольку  Пусть
Пусть  - произвольный элемент из
- произвольный элемент из  Тогда справедливо свойство 4 полугруппы
Тогда справедливо свойство 4 полугруппы  , которое запишем в виде:
, которое запишем в виде:

Интегрируя последнее выражение по  находим:
находим:

Пусть далее  Если
Если  то по условию, налагаемому на оператор
то по условию, налагаемому на оператор  ,
,  принадлежит резольвентному множеству, поэтому образом
принадлежит резольвентному множеству, поэтому образом  при отображении
при отображении  является все пространство. Следовательно, для произвольного элемента
является все пространство. Следовательно, для произвольного элемента 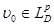
 (30)
(30)
что совпадает с (29) для 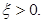 Но правая часть (30) аналитична для
Но правая часть (30) аналитична для  , поскольку справедлива оценка
, поскольку справедлива оценка  что устанавливает справедливость (29).
что устанавливает справедливость (29).
Из (29) в частности, следует, что полуплоскость  принадлежит резольвентному множеству оператора
принадлежит резольвентному множеству оператора  и
и

Допустим теперь, что операторы  порождают одну полугруппу
порождают одну полугруппу  Тогда из (29) следует равенство
Тогда из (29) следует равенство

которое означает не только совпадение резольвент операторов  но и совпадение областей значений резольвент, представляющих собой области определения операторов
но и совпадение областей значений резольвент, представляющих собой области определения операторов  Таким образом,
Таким образом,  и, следовательно, различные операторы порождают различные полугруппы.
и, следовательно, различные операторы порождают различные полугруппы.
Условия, наложенные на оператор  , оказываются достаточными для того, чтобы оператор
, оказываются достаточными для того, чтобы оператор  был инфинитезимальным оператором сильно непрерывной полугруппы
был инфинитезимальным оператором сильно непрерывной полугруппы  с оценкой нормы
с оценкой нормы  Такая полугруппа называется сжимающей. Весь ход изложенных выше рассуждений показывает, что условия (А), (А1), (В) можно ослабить. Действительно, положим, что:
Такая полугруппа называется сжимающей. Весь ход изложенных выше рассуждений показывает, что условия (А), (А1), (В) можно ослабить. Действительно, положим, что:
(А2) Оператор  замкнут и имеет плотную в
замкнут и имеет плотную в  область определения;
область определения;
(В1) Полубесконечный интервал  принадлежит резольвентному множеству оператора
принадлежит резольвентному множеству оператора  и
и 
 (31)
(31)
здесь  – постоянная, не зависящая от
– постоянная, не зависящая от  Введем оператор
Введем оператор 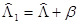 , который удовлетворяет условиям (А2), (В1), но вместо (31) выполняется неравенство
, который удовлетворяет условиям (А2), (В1), но вместо (31) выполняется неравенство

Операторнозначные функции 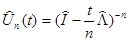 опять равномерно ограничены:
опять равномерно ограничены: 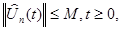 и существует сильный предел
и существует сильный предел  который представляет собой полугруппу со свойствами
который представляет собой полугруппу со свойствами 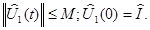 Отсюда легко видеть, что полугруппа
Отсюда легко видеть, что полугруппа  порождена оператором
порождена оператором  и удовлетворяет условиям
и удовлетворяет условиям
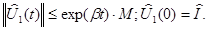 (32)
(32)
Эта полугруппа, возможно, не ограничена при  остальные свойства, полученные выше для сжимающей полугруппы, сохраняются. Полученные результаты удобно сформулировать как
остальные свойства, полученные выше для сжимающей полугруппы, сохраняются. Полученные результаты удобно сформулировать как
Теорема 1. Пусть оператор  удовлетворяет условиям (А2), (В1). Тогда он является инфинитезимальным оператором сильно непрерывной полугруппы
удовлетворяет условиям (А2), (В1). Тогда он является инфинитезимальным оператором сильно непрерывной полугруппы  с оценкой нормы (32). При этом АЗК
с оценкой нормы (32). При этом АЗК

имеет единственное решение:  для любого элемента
для любого элемента 
Замечание 1. Полугруппу  из теоремы 1 называют полугруппой класса (С0). Далее будем пользоваться этой терминологией.
из теоремы 1 называют полугруппой класса (С0). Далее будем пользоваться этой терминологией.
Замечание 2. Условия теоремы 1 относительно существования полугруппы получены нами как достаточные. На самом деле они также являются необходимыми. Этот важнейший в теории полугрупп результат носит название теоремы Хилле-Филлипса-Феллера-Миядеры.
Замечание 3. Условия (31) необходимо проверять при всех k=1,2,…. Может показаться, что достаточно выполнения условия  однако это не так для
однако это не так для  , что подтверждается контрпримерами. С другой стороны, условие
, что подтверждается контрпримерами. С другой стороны, условие
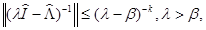 (33)
(33)
более сильное, чем условие (31), о чем говорит рассмотрение, проведенное для сжимающей полугруппы.
На основе теоремы 1 можно наметить план дальнейшего анализа задачи. Ясно, что основное внимание необходимо уделить изучению свойств оператора  в
в 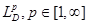 , пространствах, то есть ответить на следующие вопросы:
, пространствах, то есть ответить на следующие вопросы:
(i) Имеет ли смысл оператор  на функциях из
на функциях из 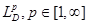 ;
;
(ii) Ограничен или нет оператор  на
на 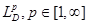 ;
;
(iii) Какова структура множества  в пространствах
в пространствах  . В частности, выполняется ли условие
. В частности, выполняется ли условие  (здесь
(здесь  - замыкание множества А); при каких значениях индекса
- замыкание множества А); при каких значениях индекса  оно справедливо;
оно справедливо;
(iv) Выполняется ли условие (31) или какой-либо из его более сильных вариантов.
Методические указания по изучению дисциплины:
1) Прочитать материалы лекции и составить краткий конспект
2) Ответить на вопросы:
· Запишите уравнение Больцмана
· Как характеризуется среда, в которой осуществляется процесс переноса нейтронов
· Какая подгруппа называется сжимающей
3) Дополнительные материалы по курсу доступны на платформе coursera по ссылке https://www.coursera.org/learn/nuclear-reactor-physics-basics#syllabus
4) Ответы и возникшие вопросы направить на адрес education-nr@mail.ru с пометкой «Теория переноса нейтронов» до 31.03.2020
5) Литература по курсу:
Макин Р.С. Нестационарная теория переноса.
Смелов В.В. Лекции по теории переноса нейтронов.
Дополнительная литература:
Макин Р.С. Нелинейные задачи теории реакторов. Газокинетическое уравнение.
Черчиньяни К. Теория и приложения уравнения Больцмана.
Кейз К., Цвайфель П. Линейная теория переноса
Литература доступна в ЭБС НИЯУ МИФИ
2. library.mephi.ru// (Электронно-библиотечная система НИЯУ МИФИ)
3. lanbook.com/ebs.php (Электронно-библиотечная система издательства «Лань»)