Головоломка «Теорема Пифагора»».
Выполнил: ученик 9 «Б» класса
Гноринский Артём Константинович
Руководитель: Савина Н.В.
2020г.
Оглавление:
Введение ………………………………………………………2стр.
ГлаваI. Теорема Пифагора и способы ее доказательства………………..4стр.
ГлаваII. Теорема Пифагора и ОГЭ………………………………………..7стр.
Раздел2.1 Теорема Пифагора в заданиях нового типа……....7стр.
Раздел2.2 Теорема Пифагора в заданиях первой части геометрия……………………………………………………...10стр.
Раздел2.3 Теорема Пифагора в заданиях второй части….....16стр.
ГлаваIII. Практическая часть. Изготовление головоломки……………...19стр.
Заключение…………………………………………………….21стр.
Список использованной литературы…………………………22стр.
Приложение……………………………………………………23стр.
Введение
Различные настольные игры и головоломки всегда находили отклик, не только в сердцах детей, но и у старшего поколения: лото, домино, пасьянсы, монополия, карты, пазлы… Сейчас настольные игры и головоломки переживают настоящий бум, на рынке появляется огромный выбор. Однако первенство остается, конечно же, за виртуальными играми.
Мне очень нравиться решать головоломки в телефоне, это достаточно удобно и интересно. Два года назад я наткнулся на игру, которая называется «Пифагор». Суть игры состояла в том, чтобы уложить геометрические фигуры из двух квадратов в один большой, перемещая и вращая их. Игра имела несколько разновидностей разбиения этих самых квадратов на другие геометрические фигуры. В восьмом классе, когда мы стали проходить теорему Пифагора, я вспомнил о своей игре и ее названии, однако способ доказательства, который мы использовали на уроке, не вносил ясности в принцип устройства игры, меня это очень заинтересовало, и я захотел в этом разобраться.
|
|
Окунувшись в этот вопрос, мне удалось узнать, что существует огромное множества доказательств данной теоремы. На уроке, мы рассмотрели только несколько способов, однако в игре, доказательство было основано на свойстве равновеликих фигур.
У меня так же есть младший брат, Илья, который учиться во втором классе, он очень любит настольные игры и мне захотелось показать ему эту игру, она его тоже очень увлекла, но родители ограничивают его время пребывания за компьютером и телефоном, конечно же и я сам понимаю, что это вредно в его возрасте. В преддверии его дня рождения, мне захотелось смастерить ему настольную головоломку похожую на виртуальную игру.
Актуальность моего проекта состоит в том, что людей всегда интересовал вопрос о теореме Пифагора и о различных способах её доказательства. Причина такой популярности теоремы: это простота, красота и широкая значимость. В современных школьных учебниках рассматриваются традиционные доказательства теоремы Пифагора. Постепенно, появлялись новые способы доказательства теорем. В моей головоломке, будет отражен другой способ доказательства, по сравнению с материалом из учебника.
Теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы свидетельствует о гигантском числе ее конкретных реализаций, поэтому эта тема и стала основой для моего проекта.
|
|
Также в учебнике геометрии теорема пифагора применяется в теории и для решения задач, мне хотелось бы увидеть, реализацию теоремы Пифагора в жизни, на примере материального объекта.
И конечно же для меня, как для девятиклассника, данная теорема актуальна еще и тем, что она есть в заданиях основного государственного экзамена
Цели и задачи:
Цель моего проекта состоит в том, чтобы изготовить головоломку, в которой показывается один из способов доказательства теоремы Пифагора, и которая будет работать по тем же принципам, что и виртуальная игра.
Задачи:
1) Рассмотреть различные способы доказательства теоремы Пифагора.
2) Проанализировать, в каких заданиях ОГЭ находит применение данная теорема.
3) Создание макета.
Гипотеза: изготовленный мною макет, будет наглядно демонстрировать выполнение теоремы Пифагора.
ГлаваI. Теорема Пифагора и способы ее доказательства
В школьном учебнике приведен следующий способ доказательства теоремы Пифагора основанный на метрических соотношениях прямоугольного треугольника:
Доказательство: На рисунке изображен прямоугольный треугольник АВС(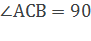
о). Докажем, что
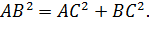
Проведя высоту CD. Применив теорему о метрических соотношениях прямоугольного треугольника для катетов АС и ВС, получаем: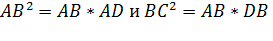 
Сложим почленно эти равенства, получим:
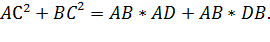
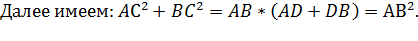
Если в прямоугольном треугольнике длины катетов равны a и b, а длина гипотенузы равна с, то по теорему Пифагора можно выразить следующим равенством: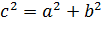 
Данный способ доказательства мне был понятен и логичен, однако я не понимал связь с моей головоломкой. Ведь она носила одноименное название. Для наглядности приведу в пример интерфейс программы.
|
|
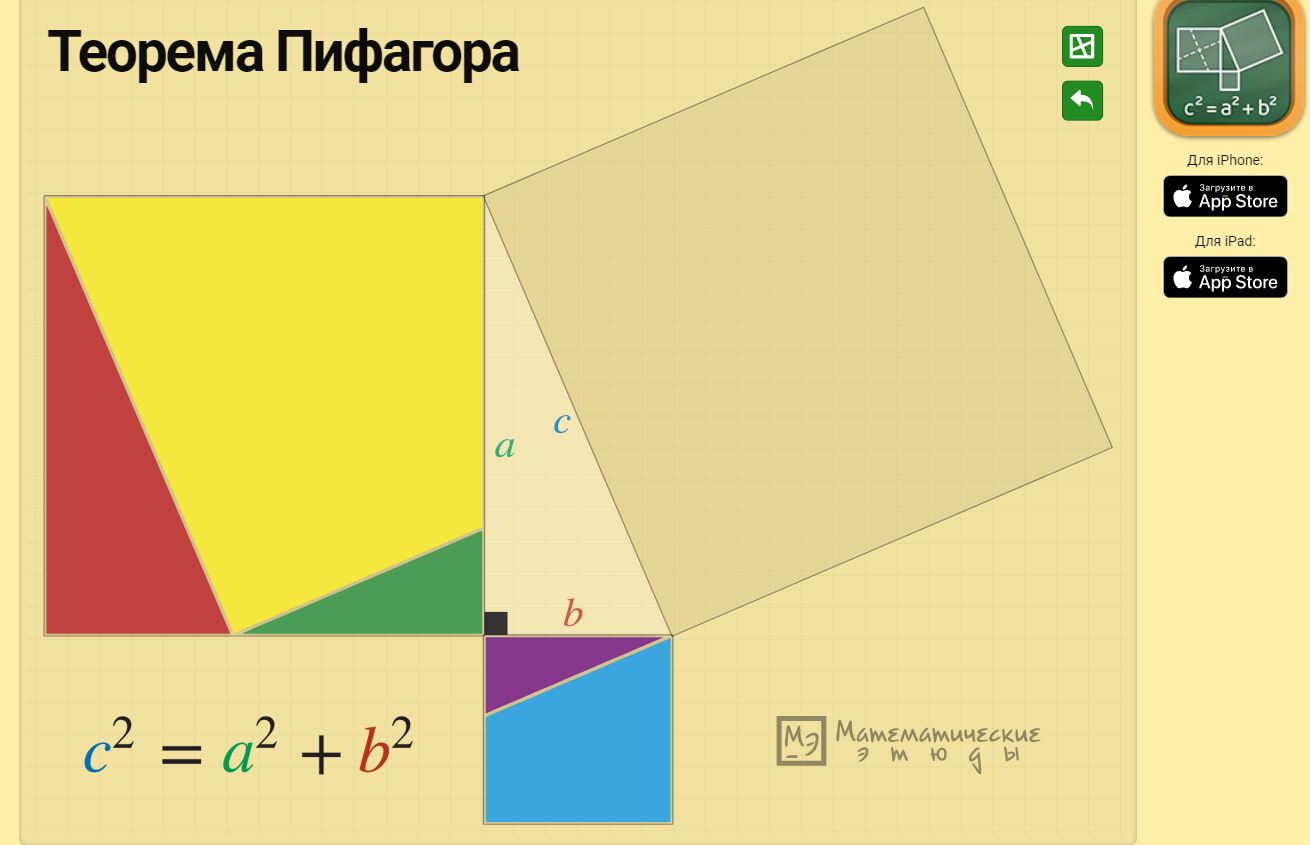
На следующий урок нам рассказали еще одни из способов доказательства данной теоремы, основанный на методе площадей.
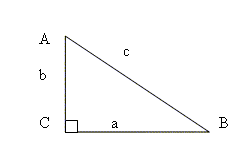Дано: прямоугольный треугольник АВС, ВС=a, АС=b и АВ=с
Доказать: с2 = а2 + в2
Доказательство
Достроим этот треугольник до квадрата со стороной a+b следующим образом.
Продолжим стороны АС и ВС за точки А и В соответственно, от точки А на продолжении стороны АС отложим отрезок, равный а, а от точки В на продолжении стороны ВС отрезок, равный b. Обозначим полученные точки D и E соответственно. Через Е проведём прямую, параллельную АС, а через точку D прямую, параллельную СВ. Обозначим точку пересечения проведённых прямых за F. От точки F на отрезке DF отложим отрезок, равный а, а на отрезке FE, отрезок, равный b. Обозначим получившиеся точки М и К соответственно. Проведём отрезки АМ, МК и ВК.
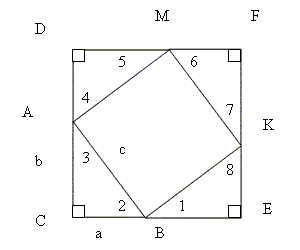
Полученный квадрат состоит из 4 равных прямоугольных треугольников (по 2 катетам) и одного четырёхугольника – квадрата (все стороны и все углы равны: каждый угол четырёхугольника равен 1800 минус сумма углов, например 2 и 3, т.е. они равны 900)
Площадь большого квадрата равна (a+b)2, а с другой стороны с2 +2(ab). Т.е. получили равенство: (a+b)2= с2 +2(ab). После раскрытия скобок и упрощения получим с2 = а2 + в2,что и требовалось доказать
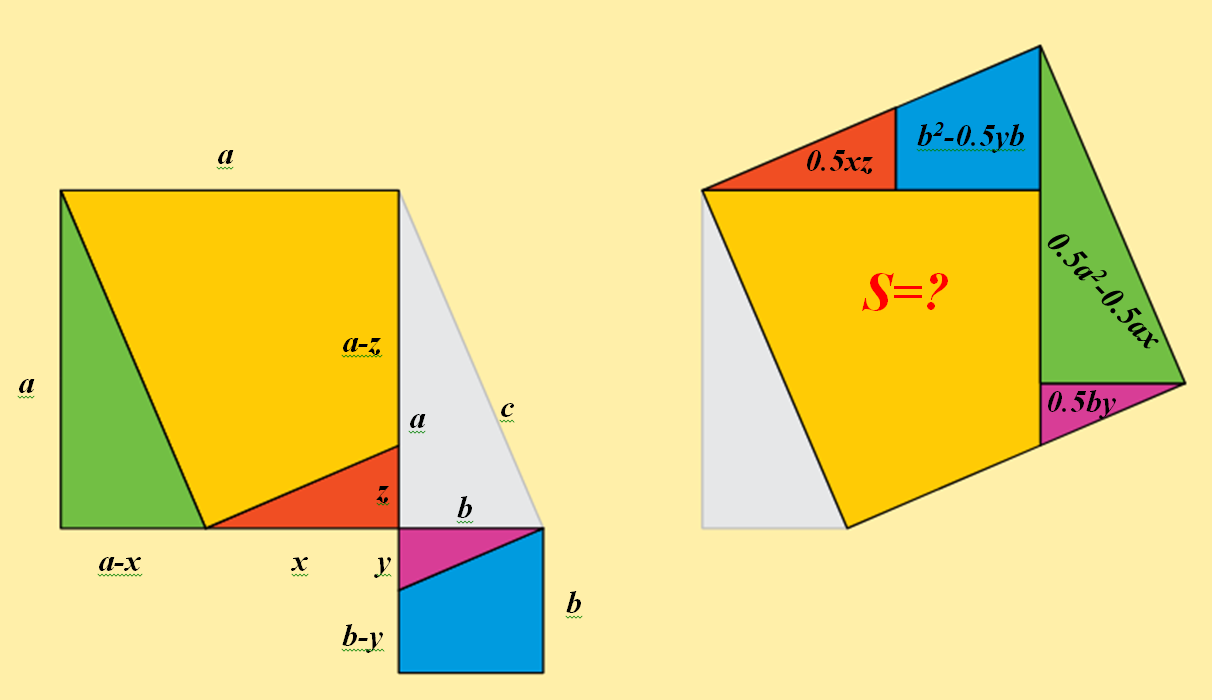Это доказательство помогло понять мне, что для логического обоснования принципа работы головоломки необходимо воспользоваться именно понятием площади. Но, при попытки доказательства, я зашел в тупик с желтым четырехугольником, поскольку формулы для поиска площади произвольного четырехугольника я не знал.
Тогда я обратился к альтернативным источникам информации, таким как интернет, на сайте где располагается данная игра, есть теоремы, изучив которые, я смог понять принцип работы данной головоломки.
Теорема (Бойаи, 1832; Гервин, 1833). Если два многоугольника равновелики, то они равносоставлены.
То есть, если два многоугольника имеют одинаковую площадь, то любой из них можно разрезать на конечное число частей, из которых в ином расположении можно составить второй многоугольник. Именно с помощью этой теоремы, можно обосновать принцип работы данной головоломки.
S среднего квадрата равна а2, S меньшего b2, данные квадраты разрезают на конечное число частей и переставляют в другом положении, в результате получается большой квадрат, S которого равна с2. Следовательно, по выше приведенной теореме, S большого квадрата= S среднего и малого, т. е. с2=а2+b2 ч.т.д.