Основная идея сезонной декомпозиции проста. В общем случае временной ряд типа того, который описан выше, можно представить себе состоящим из четырех различных компонент: (1) сезонной компоненты (обозначается St, где t обозначает момент времени), (2) тренда (Tt), (3) циклической компоненты (Ct) и (4) случайной, нерегулярной компоненты или флуктуации (It). Разница между циклической и сезонной компонентой состоит в том, что последняя имеет регулярную (сезонную) периодичность, тогда как циклические факторы обычно имеют более длительный эффект, который к тому же меняется от цикла к циклу. В методе Census I тренд и циклическую компоненту обычно объединяют в одну тренд-циклическую компоненту (TCt). Конкретные функциональные взаимосвязи между этими компонентами могут иметь самый разный вид. Однако, можно выделить два основных способа, с помощью которых они могут взаимодействовать: аддитивно и мультипликативно:
Аддитивная модель:
Xt = TCt + St + It
Мультипликативная модель:
Xt = Tt*Ct*St*It
Здесь Xt обозначает значение временного ряда в момент времени t. Если имеются какие-то априорные сведения о циклических факторах, влияющих на ряд (например, циклы деловой конъюнктуры), то можно использовать оценки для различных компонент для составления прогноза будущих значений ряда. (Однако для прогнозирования предпочтительнее экспоненциальное сглаживание, позволяющее учитывать сезонную составляющую и тренд.)
Аддитивная и мультипликативная сезонность. Рассмотрим на примере различие между аддитивной и мультипликативной сезонными компонентами. График объема продаж детских игрушек, вероятно, будет иметь ежегодный пик в ноябре-декабре, и другой - существенно меньший по высоте - в летние месяцы, приходящийся на каникулы. Такая сезонная закономерность будет повторяться каждый год. По своей природе сезонная компонента может быть аддитивной или мультипликативной. Так, например, каждый год объем продаж некоторой конкретной игрушки может увеличиваться в декабре на 3 миллиона долларов. Поэтому вы можете учесть эти сезонные изменения, прибавляя к своему прогнозу на декабрь 3 миллиона. Здесь мы имеем аддитивную сезонность. Может получиться иначе. В декабре объем продаж некоторой игрушки может увеличиваться на 40%, то есть умножаться на множитель 1.4. Это значит, например, что если средний объем продаж этой игрушки невелик, то абсолютное (в денежном выражении) увеличение этого объема в декабре также будет относительно небольшим (но в процентном исчислении оно будет постоянным); если же игрушка продается хорошо, то и абсолютный (в долларах) рост объема продаж будет значительным. Здесь опять, объем продаж возрастает в число раз, равное определенному множителю, а сезонная компонента, по своей природе, мультипликативная компонента (в данном случае равная 1.4). Если перейти к графикам временных рядов, то различие между этими двумя видами сезонности будет проявляться так: в аддитивном случае ряд будет иметь постоянные сезонные колебания, величина которых не зависит от общего уровня значений ряда; в мультипликативном случае величина сезонных колебаний будет меняться в зависимости от общего уровня значений ряда.
Аддитивный и мультипликативный тренд-цикл. Рассмотренный пример можно расширить, чтобы проиллюстрировать понятия аддитивной и мультипликативной тренд-циклических компонент. В случае с игрушками, тренд "моды" может привести к устойчивому росту продаж (например, это может быть общий тренд в сторону игрушек образовательной направленности). Как и сезонная компонента, этот тренд может быть по своей природе аддитивным (продажи ежегодно увеличиваются на 3 миллиона долларов) или мультипликативным (продажи ежегодно увеличиваются на 30%, или возрастают в 1.3 раза). Кроме того, объем продаж может содержать циклические компоненты. Повторим еще раз, что циклическая компонента отличается от сезонной тем, что она обычно имеет большую временную протяженность и проявляется через неравные промежутки времени. Так, например, некоторая игрушка может быть особенно "горячей" в течение летнего сезона (например, кукла, изображающая персонаж популярного мультфильма, которая к тому же агрессивно рекламируется). Как и в предыдущих случаях, такая циклическая компонента может изменять объем продаж аддитивно, либо мультипликативно.
12. Слияние сглаживания на сезонную составляющую ряда.
Обязательным элементом любой методики прогнозирования сезонных колебаний цен является количественная оценка сезонной составляющей, которая зависит от выбранного характера сезонности. Алгоритм расчета сезонной компоненты в случае аддитивной модели, принятой для прогнозирования цен на пиносол, состоит из следующих шагов [3]:
1. Для оценки совокупного эффекта сезонности и случайности рассчитываются отклонения фактически сложившихся цен от уровней сглаженного ряда 2. Для элиминирования влияния случайных факторов определяются предварительные оценки сезонной составляющей SEt путем усреднения значений pt для одноименных месяцев (табл.3, гр.7 и табл.4, гр.7).
3. Проводится корректировка первоначальных значений сезонной составляющей, обусловленная тем, что суммарное воздействие сезонности на динамику цен должно быть нейтральным. В связи с этим для аддитивной модели сумма значений сезонной составляющей для полного сезонного цикла должна быть равна нулю. Поэтому скорректированные оценки сезонной компоненты определяются с помощью следующего выражения:
| (8) |
| где | 
| (9) |
Окончательные оценки сезонной составляющей в табл. 3, гр. 8 и табл. 4, гр.8.
Для мультипликативной формы сезонности меняется содержание первого и третьего этапов алгоритма. Сначала вместо абсолютных отклонений рассчитываются индексы сезонности путем отношения фактически сложившихся цен к соответствующим уровням сглаженного ряда:
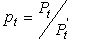
| (10) |
После получения предварительных оценок сезонности на втором шаге осуществляется их корректировка. Взаимопогашаемость сезонных колебаний в мультипликативной форме выражается в том, что средняя арифметическая из значений индексов сезонности для полного сезонного цикла должна быть равна 1. В связи с этим окончательные оценки сезонной компоненты определяются с помощью выражения:
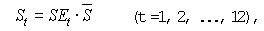
| (11) |
где
| где | 
| (12) |
13. Дисперсия, частота пересечения нуля, частота пиков.
В любом из методов прогнозирования временных рядов собственно прогноз представляет собой, по существу, оценку ожидаемого распределения результатов наблюдений в будущем. Для того чтобы на основе полученного прогноза можно было принимать решение, в большинстве случаев необходимо знать исходное распределение. Если это распределение описывается стандартной функцией, то, определив один или два его параметра, можно оценить вероятности возможных результатов будущих наблюдений.
^ 5.1. Вид распределения вероятностей
Для целей формального анализа часто удобно принимать предположения о том, что помеха (ошибка) в исходных данных подчиняется нормальному закону распределения. Однако это предположение нельзя считать обоснованным для любых реальных наблюдении. Дело в том, что распределение шума нередко асимметрично и может иметь две моды или большее количество мод. Даже когда распределение симметрично относительно единственной моды, эксцесс плотности распределения может сильно отличаться от 3.
Прогнозируемая выходная переменная характеризуется распределением, дисперсия которого зависит от дисперсии шума в исходных данных. Однако, поскольку прогнозы вычисляются на основе результатов многих наблюдений, входная переменная обычно описывается нормальным законом распределения независимо от того, каков вид распределения, описывающего шум в исходных данных.
Распределение ошибок при прогнозировании зависит как от распределения самой выходной переменной, так и от распределения соответствующего ей шума, который обычно считается не зависящим от шума в исходных данных. При прогнозировании суммы значений переменной интенсивности в течение времени упреждения, которое намного больше интервала между наблюдениями, распределение ошибок представляет собой распределение суммы выборок из нескольких таких распределений и с возрастанием времени упреждения все более и более стремится к нормальному.
^ 5.2. Дисперсия ошибок прогноза
В большинстве случаев, представляющих практический интерес, исходное распределение может быть восстановлено из полученного по прогнозу среднего значения и какого-либо другого параметра, характеризующего распределение выходной переменной. В качестве такого параметра, как правило, выбирается стандартное отклонение.
Если имеется какой-то набор прогнозируемых временных рядов, то обычно оказывается, что для каждого ряда существует определенная зависимость между разбросом ошибок и уровнем прогноза. Например, хотя объемы производства пшеницы (аw) и риса (аr), прогнозируемые па данный год, могут сильно отличаться друг от друга, между прогнозами производства разных зерновых культур существует четкая корреляция в соответствии с соотношением 
, где параметры µ и α представляют собой характеристики всего семейства прогнозов зерновых. Этот же результат справедлив и для прогнозов спроса на различные предметы, относящиеся к одному и тому же классу. Отсюда следует, что, исходя из всего семейства прогнозов, можно оценивать параметры µ и α использовать связывающее их соотношение в целях установления стандартного отклонения распределения ошибок для любых отдельных рядов.
Другое соотношение между величиной а и параметрами о, µ и α (о²= % (о2 = µа + αа²) было предложено в работе, а основы анализа процессов, описываемых подобными соотношениями, рассмотрены в работе.
Среднее абсолютное отклонение представляет собой оценку отклонений, которая имела бы место, если бы прогнозы разрабатывались на основе минимизации суммы абсолютных величин остаточных разностей между результатами наблюдений и медианой распределения вместо обычно проводимой минимизации суммы квадратов отклонений от среднего. При появлении методов исследования операций, когда возможности обработки данных были ограничены, среднее абсолютное отклонение использовалось вместо стандартного отклонения только потому, что его вычисление требовало меньше времени и меньшего объема памяти. Особенно широко этот показатель использовался в программах ЭВМ для прогнозирования спроса. Однако при достаточно высоком быстродействии и большой емкости памяти современных ЭВМ применение среднего абсолютного отклонения нецелесообразно.
Если распределение описывается нормальным законом, то среднее абсолютное отклонение т = 0,8о (точное значение коэффициента при о равно √ 2/л = 0,7979). Для других распределений аналогичное соотношение может иметь иной вид. Так как средняя ошибка прогноза должна быть равна нулю, то дисперсия определяется среднеквадратичной ошибкой. Выбрав подходящую модель процесса, которая математически может быть выражена, например, либо константой, либо через линейные и сезонные составляющие, либо дисперсию, можно пересматривать значения коэффициентов этой модели по среднеквадратичной ошибке каждый раз, когда поступает новая информация и заново измеряется ошибка прогноза.
Если шум результатов наблюдений автокоррелирован незначительно, то дисперсия ошибок прогноза переменной интенсивности в течение времени упреждения будет равна сумме дисперсий ошибок прогнозов для отдельных интервалов, на которые разбивается время упреждения L с целью периодического уточнения прогноза. Следовательно, стандартное отклонение, используемое для принятия решений, приблизительно равно o\/ L. В тех случаях, когда имеет место автокоррелящш шума, выражение для стандартного отклонения может быть записано в виде 
, где 
— стандартное отклонение ошибок одного знака, L — время упреждения, измеренное в интервалах между проверками прогноза, и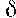 
— постоянная, которая является характеристикой всего семейства прогнозируемых рядов.
14. Метод переменных разностей.
Предварительный анализ рядов показывает 5-ю степень гладкости полиномиального тренда Для метода разделенных разностей рассчитываем конечные разности Vn, где
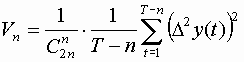
Затем рассчитываем
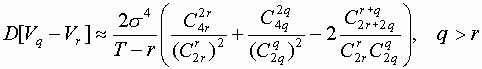
где вместо s2 берем оценку Vq.
Тогда можно построить статистику
при этом 
Далее строим критическую область, где берем a = 0,05. Если статистика u не попадает в критическую область, то основная гипотеза Н0 (вследствие которой берем степень тренда, равную qmax) не отвергается, и мы продолжаем наши исследования гладкости тренда по методу разделенных разностей.
15. Обнаружение сезонных колебаний.
В статистике существует ряд методов изучения и измерения сезонных колебаний. Самый простой заключается в построении специальных показателей, которые называются индексами сезонности iS. Совокупность этих показателей отражает сезонную волну.
В общем виде они определяются отношением исходных (эмпирических) уровней ряда динамики 
к теоретическим (расчетным) уровням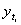 
, выступающим в качестве базы сравнения:
. (2.1)
Именно в результате того, что в этой формуле измерение сезонных колебаний производится на базе соответствующих теоретических уровней тренда 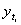, в исчисляемых при этом индивидуальных индексах сезонности влияние основной тенденции развития элиминируется (устраняется).
Для того чтобы выявить устойчивую сезонную волну, на которой не отражались бы случайные условия одного года, индексы сезонности вычисляют по данным за несколько лет (не менее трех), распределенным по месяцам.
Поскольку на сезонные колебания могут накладываться случайные отклонения, для их устранения производится усреднение индивидуальных индексов одноименных внутригодовых периодов анализируемого ряда динамики. Поэтому для каждого периода годового цикла определяются обобщенные показатели в виде средних индексов сезонности 
:
. (2.2)
Вычисленные на основе этой формулы средние индексы сезонности (с применением в качестве базы сравнения соответствующих уровней тренда) свободны от влияния основной тенденции развития и случайных отклонений.
В зависимости от характера тренда формула (2.2) принимает следующие формы:
1) для рядов внутригодовой динамики с ярко выраженной основной тенденцией развития
. (2.3)
Выступающие при этом в качестве переменной базы сравнения теоретические уровни 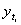представляют своего рода "среднюю ось кривой", так как их расчет основан на положениях метода наименьших квадратов. Поэтому измерение сезонных колебаний на базе переменных уровней тренда называется способом переменной средней;
2) для рядов внутригодовой динамики, в которых повышающийся (снижающийся) тренд отсутствует или он незначителен
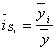. (2.4)
В формуле (2.4) базой сравнения является общий для анализируемого ряда динамики средний уровень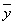 
. Поскольку для всех эмпирических уровней анализируемого ряда динамики этот общий средний уровень является постоянной величиной, то применение формулы (2.4) называется способом постоянной средней.
Для наглядного представления сезонной волны исчисленные индексы сезонности изображают в виде графика (линейной диаграммы).
Для определения в формуле (2.1) теоретических уровней тренда 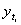важно правильно подобрать математическую функцию, по которой будет производиться аналитическое выравнивание в анализируемом ряду динамики. Это наиболее сложный и ответственный этап изучения сезонных колебаний. От обоснованности подбора той или иной математической функции во многом зависит практическая значимость получаемых в анализе индексов сезонности.
При использовании способа аналитического выравнивания ход вычислений индексов сезонности следующий:
- по соответствующему полиному вычисляются для каждого месяца (квартала) выравненные уровни на момент времени t;
- определяются отношения фактических месячных (квартальных) данных к соответствующим выравненным данным (в процентах);
- находятся средний арифметические из процентных соотношений, рассчитанных по одноименным периодам в процентах.
Расчет заканчивается проверкой правильности вычислений индексов. Так как средний индекс сезонности для всех месяцев (кварталов) должен быть 100%, то сумма полученных индексов по месячным данным равна 1200, а сумма по четырем кварталам – 400.
16. Аддитивные и мультипликативные сезонные индексы.
Уровни временного ряда являются суммой двух составляющих:
1. систематической (детерминированной, регулярной)
2. случайной (нерегулярной, непредсказуемой), не зависящей от времени
Регулярная составляющая, в общем случае, может складываться из тренда, циклической компоненты и сезонной компоненты. Однако, регулярная составляющая не обязательно должна включать все три компоненты.
Случайная (нерегулярная) компонента. Экономисты разделяют факторы, под действием которых формируется нерегулярная компонента, на 2 вида:
1. факторы резкого, внезапного действия;
2. текущие факторы.
Первый тип факторов (например, стихийные бедствия, эпидемии и др.), как правило, вызывает более значительные отклонения по сравнению со случайными колебаниями – иногда такие отклонения называют катастрофическими колебаниями.
Факторы второго типа вызывают случайные колебания, являющиеся результатом действия большого числа побочных причин. Влияние каждого из текущих факторов незначительно, но ощущается их суммарное воздействие.
Цель сезонной декомпозиции и корректировки временного ряда состоит в том, чтобы разложить ряд на составляющие: тренд, сезонную компоненту и нерегулярную составляющую.
В общем случае временной ряд можно представить из четырех различных компонент:
1. сезонной компоненты (обозначается St, где t обозначает момент времени)
2. тренда (Tt)
3. циклической компоненты (Ct)
4. случайной, нерегулярной компоненты (Et)
Разница между циклической и сезонной компонентой состоит в том, что последняя имеет регулярную (сезонную) периодичность, тогда как циклические факторы обычно имеют более длительный эффект, который, к тому же, меняется от цикла к циклу. Тренд и циклическую компоненту обычно объединяют в одну тренд-циклическую компоненту (TtCt) (для простоты обозначений далее TtCt–>Tt). Конкретные функциональные взаимосвязи между этими компонентами могут иметь самый разный вид. Однако можно выделить два основных способа, с помощью которых они могут взаимодействовать - аддитивно и мультипликативно:
- Аддитивная модель: Уt = TCt + St + Et
- Мультипликативная модель: Уt = Tt*Ct*St*Et
- Модель смешанного типа: Уt = Tt*Ct*St+Et
Выбор одной из трех моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянными для различных циклов. Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты. Построениеаддитивнойимультипликативной моделей сводится к расчету значений T, S и E для каждого уровня ряда. Процесс построения модели включает в себя следующие шаги:
1. Выравнивание исходного ряда методом скользящей средней.
2. Расчет значений сезонной компоненты S.
3. Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных (Y – S=T + E) в аддитивной или (Y: S=T * E) в мультипликативной модели.
4. Аналитическое выравнивание уровней (T + E) или (T * E) и расчет значений T с использованием полученного уравнения тренда.
5. Расчет полученных по модели значений (T + E) или (T * E).
6. Расчет абсолютных и/или относительных ошибок. Если из временного ряда удалить тренд (Tt) и периодические составляющие (Ct и St), то останется нерегулярная компонента (Et), так называемая, ошибка. Если полученные значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни ряда и в дальнейшем использовать временной ряд ошибок (Et) для анализа взаимосвязи исходного ряда и других временных рядов.
17. Стационарные и эргодические временные ряды.
Среди всех случайных процессов оказывается полезным выделить
такие, которые обладают дополнительным свойством стационарности,
т.е. некоторой регулярности относительно времени. Различают два
класса стационарных случайных процессов – стационарные в широком и
в узком смысле.
Случайный процесс X(t) называется стационарным (в узком, т.е.
в наиболее строгом смысле этого слова), если все его функции
распределения (F(x,t),F(x1,x2,t1,t2) и т.д.) не зависят от выбора
начальной точки отсчета времени. Другими словами, процесс
стационарен, если все его вероятностные характеристики (а эти
характеристики полностью определяются его функциями распределения
- одномерной, двумерной и т.д.) являются стационарными. Тем самым
все моменты времени тут являются равноправными.
Для одномерной функции распределения F(x,t) условие
стационарности можно записать в виде:
F(x,t+T)=F(x,t),
где T – произвольное число. Отсюда следует, что F(x,t) не зависит
от t и потому является функцией одного только x. А отсюда
вытекает, в частности, что математическое ожидание случайного
процесса (как, впрочем, и его дисперсия) является постоянной
величиной. Это означает, что стационарный процесс можно
рассматривать как состоящий из случайных колебаний вокруг
некоторого фиксированного значения, которое является его
стационарным состоянием. Графически это изображается как колебания
вокруг горизонтальной прямой.
Для двумерной функции распределения условие стационарности
можно записать в следующем виде:
F(x1,x2,t1+T,t2+T)=F(x1,x2,t1,t2).
Положив τ=t2-t1, мы видим, что двумерная функция распределения
F(x1,x2,t1,t2) фактически зависит не от моментов времени t1 и t2, а
лишь от их разности τ, называемой иногда лагом (запаздыванием,
задержкой) и может быть записана в виде F(x1,x2,τ). Отсюда следует,
что все вероятностные характеристики случайного процесса, которые
выражаются через двумерную функцию распределения, зависят от τ. В
частности, это относится к функции автокорреляции rX(s,t)=rX(τ).
Стационарные случайные процессы описывают те явления и
системы, изменения которых являются стационарными (в том смысле,
что не зависят от выбора системы отсчета времени). Например,
стационарными можно считать напряжение в линии электропередач,
давление газа в замкнутом помещении или в газопроводе и т.д.
Кроме независимости MX от t и зависимости KX только от τ стационарные случайные процессами обладают еще многими дополнительными свойствами. Дело в том, что выше мы не
использовали еще многие другие числовые характеристики случайных процессов, которые выражаются через одно- и двумерную функции распределения (среди которых и такие важные, как дисперсия), а о функциях распределения высших порядков речь вообще не шла. Однако в процессе практического изучения тех случайных процессов и временных рядов, которые есть основания рассматривать как стационарные, оказалось, что именно указанные выше две особенности стационарных процессов являются определяющими. Поэтому было введено понятие стационарности в широком смысле, которое основывается только на этих двух особенностях. А именно, случайный процесс X(t) называется стационарным в широком (или, лучше сказать, расширенном) смысле, если его математическое ожидание MX постоянно, а функция автоковариации KX зависит только от разности s-t временных аргументов.
Случайных процессов, стационарных в широком смысле, в природе очень много. Например, это все процессы, стационарные в узком смысле, а также, как мы сейчас покажем, и все задаваемые в виде суммы независимых элементарных гармонических процессов.
Стационарность – это не единственное полезное свойство, которым могут обладать случайные процессы и которое дает возможность более подробно их исследовать. Еще одним свойством
такого рода является эргодическое свойство или, говоря более, эргодичность. Понятие “эргодичность” заимствовано из статистической физики, в которой изучаются свойства некоторых физических систем (например, газов) состоящих из большого числа одинаковых частиц. Там выделяется особый класс систем, в которых математические ожидания (средние значения) физических характеристик можно вычислить не только путем усреднения по всему множеству составляющих систему частиц, но и по траектории движения одной единственной частицы. Термин ‘эргодический” связан с греческим словом ergon – работа, в статистической физике он появляется потому, что свойство эргодичности формулируется в тонком (в пределе – бесконечно тонком) слое фазовой области вблизи поверхности постоянной энергии. Эргодичность проявляется в том, что со временем соответствующий физический процесс становится однородным, т.е. любая реализация этого процесса окажется в какой- то момент сколь угодно близко к произвольному заданному состоянию.
18. Теорема Биркгофа-Хинчина.
Эргодическая теорема Биркгофа-Хинчина утверждает, что для динамической системы, сохраняющей меру, и интегрируемой функции на пространстве для почти всех по этой мере начальных точек соответствующие им временные средние сходятся. Более того, если инвариантная мераэргодична, то для почти всех начальных точек предел один и тот же — интеграл функции по данной мере. Этот принцип формулируется как «временное среднее для почти всех начальных точек равно пространственному». Теорема. Пусть 
-- сохраняющее меру 
отображение, и функция 
на X интегрируема по мере . Тогда временные средние 
сходятся к некоторой инвариантной функции 
: 
причём сходимость имеет место как в 
, так и почти всюду по мере .
19. Идентификация ряда скользящих средних (метод Уокера).
Идентификация. Как отмечено ранее, для модели АРПСС необходимо, чтобы ряд был стационарным, это означает, что его среднее постоянно, а выборочные дисперсия и автокорреляция не меняются во времени. Поэтому обычно необходимо брать разности ряда до тех пор, пока он не станетстационарным (часто также применяют логарифмическое преобразование для стабилизации дисперсии). Число разностей, которые были взяты, чтобы достичь стационарности, определяются параметром d (см. предыдущий раздел). Для того чтобы определить необходимый порядок разности, нужно исследовать график ряда и автокоррелограмму. Сильные изменения уровня (сильные скачки вверх или вниз) обычно требуют взятия несезонной разности первого порядка (лаг= 1). Сильные изменения наклона требуют взятия разности второго порядка. Сезонная составляющая требует взятия соответствующей сезонной разности (см. ниже). Если имеется медленное убывание выборочных коэффициентов автокорреляции в зависимости от лага, обычно берут разность первого порядка. Однако следует помнить, что для некоторых временных рядов нужно брать разности небольшого порядка или вовсе не брать их. Заметим, что чрезмерное количество взятых разностей приводит к менее стабильным оценкам коэффициентов.
На этом этапе (который обычно называют идентификацией порядка модели, см. ниже) вы также должны решить, как много параметров авторегрессии (p) и скользящего среднего (q) должно присутствовать в эффективной и экономной модели процесса. (Экономность модели означает, что в ней имеется наименьшее число параметров и наибольшее число степеней свободы среди всех моделей, которые подгоняются к данным). На практике очень редко бывает, что число параметров p или q больше 2 (см. ниже более полное обсуждение).
Число оцениваемых параметров. Конечно, до того, как начать оценивание, вам необходимо решить, какой тип модели будет подбираться к данным, и какое количество параметров присутствует в модели, иными словами, нужно идентифицировать модель АРПСС. Основными инструментами идентификации порядка модели являются графики, автокорреляционная функция (АКФ), частная автокорреляционная функция (ЧАКФ). Это решение не является простым и требуется основательно поэкспериментировать с альтернативными моделями. Тем не менее, большинство встречающихся на практике временных рядов можно с достаточной степенью точности аппроксимировать одной из 5 основных моделей (см. ниже), которые можно идентифицировать по виду автокорреляционной (АКФ) и частной автокорреляционной функции (ЧАКФ). Ниже дается список этих моделей, основанный на рекомендациях Pankratz (1983); дополнительные практические советы даны в Hoff (1983), McCleary and Hay (1980), McDowall, McCleary, Meidinger, and Hay (1980), and Vandaele (1983). Отметим, что число параметров каждого вида невелико (меньше 2), поэтому нетрудно проверить альтернативные модели.
1. Один параметр (p):АКФ - экспоненциально убывает; ЧАКФ - имеет резко выделяющееся значение для лага 1, нет корреляций на других лагах.
2. Два параметра авторегрессии (p): АКФ имеет форму синусоиды или экспоненциально убывает; ЧАКФ имеет резко выделяющиеся значения на лагах 1, 2, нет корреляций на других лагах.
3. Один параметр скользящего среднего (q): АКФ имеет резко выделяющееся значение на лаге 1, нет корреляций на других лагах. ЧАКФ экспоненциально убывает.
4. Два параметра скользящего среднего (q): АКФ имеет резко выделяющиеся значения на лагах 1, 2, нет корреляций на других лагах. ЧАКФ имеет форму синусоиды или экспоненциально убывает.
5. Один параметр авторегрессии (p) и один параметр скользящего среднего (q): АКФ экспоненциально убывает с лага 1; ЧАКФ - экспоненциально убывает с лага 1.
Сезонные модели. Мультипликативная сезонная АРПСС представляет естественное развитие и обобщение обычной модели АРПСС на ряды, в которых имеется периодическая сезонная компонента. В дополнении к несезонным параметрам, в модель вводятся сезонные параметры для определенного лага (устанавливаемого на этапе идентификации порядка модели). Аналогично параметрам простой модели АРПСС, эти параметры называются: сезонная авторегрессия (ps), сезонная разность (ds) и сезонное скользящее среднее (qs). Таким образом, полная сезонная АРПСС может быть записана как АРПСС (p, d, q)(ps, ds, qs). Например, модель (0,1,2)(0,1,1) включает 0 регулярных параметров авторегрессии, 2 регулярных параметра скользящего среднего и 1 параметр сезонного скользящего среднего. Эти параметры вычисляются для рядов, получаемых после взятия одной разности с лагом 1 и далее сезонной разности. Сезонный лаг, используемый для сезонных параметров, определяется на этапе идентификации порядка модели.
Общие рекомендации относительно выбора обычных параметров (с помощью АКФ и ЧАКФ) полностью применимы к сезонным моделям. Основное отличие состоит в том, что в сезонных рядах АКФ и ЧАКФ имеют существенные значения на лагах, кратных сезонному лагу (в дополнении к характерному поведению этих функций, описывающих регулярную (несезонную) компоненту АРПСС).
15 Тема. Прогнозирование и планирование на основе методов математического программирования.
1. Модели математического программирования и их использование для построения оптимальных планов
Математическое программирование — область математики, разрабатывающая теорию и численные методы решения многомерных экстремальных задач с ограничениями, т. е. задач на экстремум функции многих переменных с ограничениями на область изменения этих переменных.
Функцию, экстремальное значение которой нужно найти в условиях экономических возможностей, называют целевой, показателем эффективности или критерием оптимальности. Экономические возможности формализуются в виде системы ограничений. Все это составляет математическую модель. Математическая модель задачи — это отражение оригинала в виде функций, уравнений, неравенств, цифр и т. д. Модель задачи математического программирования включает:
1) совокупность неизвестных величин, действуя на которые, систему можно совершенствовать. Их называют планом задачи (вектором управления, решением, управлением, стратегией, поведением и др.);
2) целевую функцию (функцию цели, показатель эффективности, критерий оптимальности, функционал задачи и др.). Целевая функция позволяет выбирать наилучший вариант - из множества возможных. Наилучший вариант доставляет целевой функции экстремальное значение. Это может быть прибыль, объем выпуска или реализации, затраты производства, издержки обращения, уровень обслуживания или дефицитности, число комплектов, отходы и т. д.;
Эти условия следуют из ограниченности ресурсов, которыми располагает общество в любой момент времени, из необходимости удовлетворения насущных потребностей, из условий производственных и технологических процессов. Ограниченными являются не только материальные, финансовые и трудовые ресурсы. Таковыми могут быть возможности технического, технологического и вообще научного потенциала. Нередко потребности превышают возможности их удовлетворения. Математически ограничения выражаются в виде уравнений и неравенств. Их совокупность образует область допустимых решений (область экономических возможностей). План, удовлетворяющий системе ограничений задачи, называется допустимым. Допустимый план, доставляющий функции цели экстремальное значение, называется оптимальным. Оптимальное решение, вообще говоря, не обязательно единственно, возможны случаи, когда оно не сущес