Задача №2. Множественный регрессионный анализ.

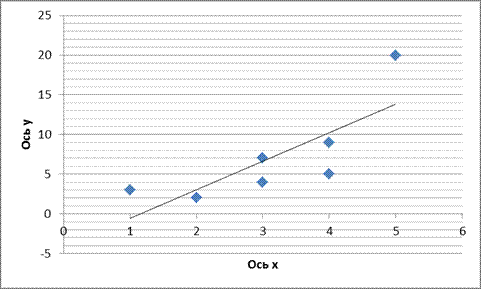
2.1 Нанести в координатах х₂у точки на плоскость (построить корреляционное поле).

Решение. Для наглядности выберем наши данные из табл. 1 и 2. Из рис. 2 видно, что прямая линия хорошо аппроксимирует связь между у и х₂. Эта связь прямая и очень тесная.

 

2.2. Записать для своего варианта матрицу Х значений объясняющих переменных (матрицу плана).

Решение:

 

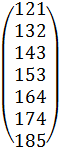
2.3. Записать транспонированную матрицу плана .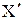

Решение:

 

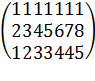
2.4. Найти произведение матриц .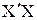

Решение:

 

= . =

 

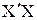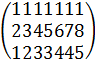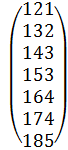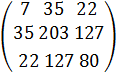
C₁₁= 1 · 1 + 1 · 1 + 1 · 1 + 1 · 1 + 1 · 1 + 1 · 1 + 1 · 1 = 1 + 1 + 1 + 1 + 1 + 1 + 1 = 7

c₁₂ = 1 · 2 + 1 · 3 + 1 · 4 + 1 · 5 + 1 · 6 + 1 · 7 + 1 · 8 = 2 + 3 + 4 + 5 + 6 + 7 + 8 = 35

c₁₃ = 1 · 1 + 1 · 2 + 1 · 3 + 1 · 3 + 1 · 4 + 1 · 4 + 1 · 5 = 1 + 2 + 3 + 3 + 4 + 4 + 5 = 22

c₂₁ = 2 · 1 + 3 · 1 + 4 · 1 + 5 · 1 + 6 · 1 + 7 · 1 + 8 · 1 = 2 + 3 + 4 + 5 + 6 + 7 + 8 = 35

c₂₂ = 2 · 2 + 3 · 3 + 4 · 4 + 5 · 5 + 6 · 6 + 7 · 7 + 8 · 8 = 4 + 9 + 16 + 25 + 36 + 49 + 64 = 203

c₂₃ = 2 · 1 + 3 · 2 + 4 · 3 + 5 · 3 + 6 · 4 + 7 · 4 + 8 · 5 = 2 + 6 + 12 + 15 + 24 + 28 + 40 = 127

c₃₁ = 1 · 1 + 2 · 1 + 3 · 1 + 3 · 1 + 4 · 1 + 4 · 1 + 5 · 1 = 1 + 2 + 3 + 3 + 4 + 4 + 5 = 22

c₃₂ = 1 · 2 + 2 · 3 + 3 · 4 + 3 · 5 + 4 · 6 + 4 · 7 + 5 · 8 = 2 + 6 + 12 + 15 + 24 + 28 + 40 = 127

c₃₃ = 1 · 1 + 2 · 2 + 3 · 3 + 3 · 3 + 4 · 4 + 4 · 4 + 5 · 5 = 1 + 4 + 9 + 9 + 16 + 16 + 25 = 80

2.5. Найти обратную матрицу (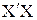)^-1.

Решение. Для краткости введем обозначение: А= 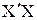. требуется найти обратную матрицу А-1. Используем формулу:

 

 

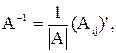
где - определитель матрицы А,

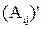– транспонированная матрица, составленная из алгебраических дополнений матрицы А.

 

/A/=7·203·80 + 35·127·22 + 22·35·127 - 22·203·22 - 7·127·127 - 35·35·80 = 113680 + 97790 + 97790 - 98252 - 112903 - 98000 = 105

Находим алгебраические дополнения:

А11=203·80 - 127·127 = 16240 - 16129 = 111;	А12 = 35·80 - 22·127 = 2800 - 2794 =- 6;
А13 = 35·127 - 22·203 = 4445 - 4466 = -21;	А21 = 35·80 - 127·22 = 2800 - 2794 =- 6;
А22 = 7·80 - 22·22 = 560 - 484 = 76;	А23 = 7·127 - 22·35 = 889 - 770 = 119;
А31 = 35·127 - 203·22 = 4445 - 4466 = -21;	А32 = 7·127 - 35·22 = 889 - 770 = -119;
А33 = 7·203 - 35·35 = 1421 - 1225 = 196.

 

Обратная матрица:

А^-1 = . =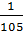

 

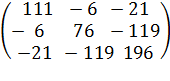Проверка. Если расчеты верны, то должно выполниться равенство:

А А^-1 = Е.

Для повышения точности множитель 1/105 введем отдельно.

 

А А^-1 = =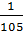

 

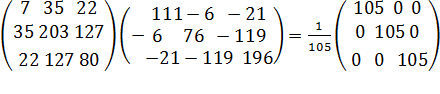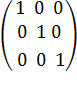
Как видно, равенство выполнено, значит расчет обратной матрицы выполнен верно.

2.6. Найти произведение матриц .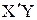

Решение.

 

= =

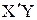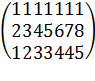
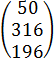
Компоненты матрицы С вычисляются следующим образом:

c₁₁ = = 1 · 3 + 1 · 2 + 1 · 4 + 1 · 7 + 1 · 5 + 1 · 9 + 1 · 20 = 3 + 2 + 4 + 7 + 5 + 9 + 20 = 50
c₂₁ = = 2 · 3 + 3 · 2 + 4 · 4 + 5 · 7 + 6 · 5 + 7 · 9 + 8 · 20 = 6 + 6 + 16 + 35 + 30 + 63 + 160 = 316
c₃₁ = = 1 · 3 + 2 · 2 + 3 · 4 + 3 · 7 + 4 · 5 + 4 · 9 + 5 · 20 = 3 + 4 + 12 + 21 + 20 + 36 + 100 = 196

 

2.7. Найти уравнение регрессии Y по Х₁ и Х₂ в форме =b₀+ b₁ х₁ + + b₂х₂ методом наименьших квадратов путем умножения матрицы (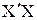.)^-1 на матрицу 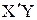, т.е. рассчитать коэффициенты регрессии по формуле b=(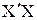)^-1 .

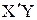Решение.

b=(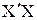)^-1 = .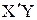

 

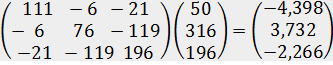
Компоненты матрицы b вычисляются следующим образом:

b11 = 111 · 50 + (-6) · 316 + (-21) · 196 = 5550 - 1896 - 4116 = -462*0,00952=-4,39824

b21 = (-6) · 50 + 76 · 316 + (-119) · 196 = (-300) + 24016 - 23324 = 392*0,00952=3,73184

b31 = (-21) · 50 + (-119) · 316 + 196 · 196 = (-1050) - 37604 + 38416 = -238*0,00952=-2,26576

 

Итак, ответ: b₀ = -4,40; b₁ = 3,73; b₂ = -2,27. Уравнение множественной регрессии имеет вид: = - 4,40 + 3,73x₁ – 2,27x₂.

 

2.8. Объяснить смысл изменения значения коэффициента регрессии b₁.

Решение. В задаче №1 значение b₁=2,36, а теперь его значение увеличилось до b₁=3,73. Это связано с тем, что на объем продаж помимо торговой площади теперь влияет учитываемая площадь паркинга.

2.9. Рассчитать значения коэффициентов эластичности для обоих факторов и сравнить влияние каждого из них на средний объем продаж.

Решение. Коэффициент эластичности в общем случае есть функция объясняющей переменной, например: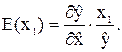

 

Если 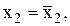то E1 = b1 * x1/ȳ =3,73*5/7,14=2,61; при увеличении х₁ от среднего на 1% объем продаж увеличится на 2,61%. Аналогично E2 = b2 * x2/ȳ = -2,27*3,14/7,14=-1%; при увеличении х₂ от среднего на 1% объем продаж уменьшится на 1%.

2.10. Оценить аналитически прогнозное среднее значение объема продаж для проектируемого магазина "СИ" с торговой площадью х₁=11 (1100 м²) и паркинговой площадью х₂ = 8 (80 автомашин).

Решение. Объем продаж рассчитаем по уравнению регрессии:

 

= -4,40 +3,73 × 11 – 2,27 × 8 = 18,47.

2.11, а) Найти 95%-ный доверительный интервал для среднего прогнозного значения объема продаж магазина "СИ".

Решение. По условию нужно оценить М_х(Y), где вектор переменных 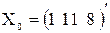Выборочной оценкой условного МOМ_х(Y) является значение регрессии (11, 8) = 18,47. Для построения доверительного интервала для М_х(Y) нужно знать дисперсию оценки 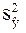и дисперсию возмущений s²:

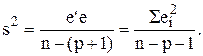
Для удобства вычислений составим табл. 5.

i	xi1	xi2	yi		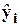ei
				0,79	2,21	4,8841
				2,25	-0,25	0,0625
				3,71	0,29	0,0841
				7,44	-0,44	0,1936
				8,9	-3,9	15,21
				12,63	-3,63	13,177
				14,09	5,91	34,928
∑				49,81	0,19	68,539

 

На основе табличных данных:

S² =68,54/(7-2-1) = 17,14; S= 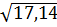=4,14

Х'₀ (Х'Х)^-1 = (1 11 8) =

(Х'₀ (Х'Х)^-1 ) Х₀ = 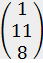= 4,187

S 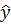=4,14 = 8,47

По табл. П2 находим критическое значение статистики Стьюдента t_{0,95; 7-2-1=5} = 2,78. Полуинтервал D = t_{0,95; 5} = 2,78 × 8,47 = 23,56.

Нижняя граница интервала: _min = _Xo - D = 18,47 – 23,56 = -5,09.

Верхняя граница интервала: _mах = _Xo + D = 18,47 + 23,56 = 42,03. Окончательно доверительный интервал для среднего прогнозного значения _Xo: -5,09 £ М_Хo(Y) £ 42,03. Интервал большой, что объясняется слишком короткой выборкой.

2.11, б) Найти 95%-ный доверительный интервал для индивидуального прогнозного значения объема продаж магазина "СИ" .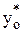

Решение. Интервал рассчитаем по выражению:

 

 

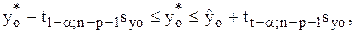
где s_yo = 4,14 =9,43

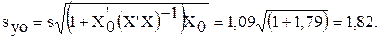
Полуинтервал D = 2,78 × 9,43 = 26,22. Нижние и верхние границы интервала: _min = 18,47 – 26,22 = -7,75 и _max = 18,47 + 26,22 = 44,69. Окончательно интервал имеет вид: -7,75 £ 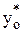£ 44,69. Как и следовало ожидать, данный индивидуальный интервал больше предыдущего среднего.

 

2.12. Проверить значимость коэффициентов регрессии.

Решение. Стандартная ошибка рассчитывается по формуле:

 

 

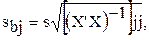
где выражение под корнем есть диагональный элемент матрицы ^-1.

Отсюда: s_b1 = 4,14 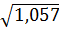= 4,26; s_b2 =4,14 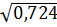= 3,52.

Так как t = çb₁ç/ s_b1 = 3,73/4,26=0,88 < t_0,95;4 = 2,78, то коэффициент b₁незначим (незначимо отличается от нуля).

Так как t = çb₂ç/ s_b2 = 2,27/3,52=0,65 < t_0,95;4 = 2,78, то и коэффициент b₂ незначим на 5%-ном уровне.

2.13. Найти с надежностью 0,95 интервальные оценки коэффициентов регрессии b₁ и b₂ и дисперсии s².

Решение. Интервалы коэффициентов регрессии рассчитываются по формуле: b_j + t_1-a,n-p-1s_bj £ b_j £ b_j + t_1-a,n-p-1s_bj.

Поскольку оба коэффициента регрессии незначимы, то не имеет смысла строить для них доверительные интервалы.

2.14. Определить множественный коэффициент детерминации и проверить значимость уравнения регрессии на уровне a=0,05.

Решение. Коэффициент детерминации рассчитывается по формуле:

 

;

 

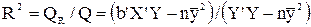
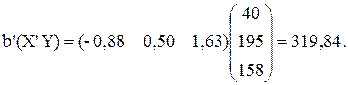
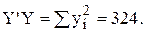
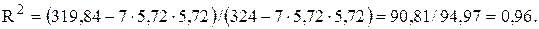
Уравнение регрессии значимо, если (критерий Фишера):

F = R² (n-p-1)/(1- R²) p > F_a;k1;k2.

Отсюда F = 0,96(7-2-1)/(1-0,962)2 = 24,62 > F_0,05;2;4.

Вывод: уравнение значимо.

2.15. Определить, существенно ли увеличилось значение коэффициента детерминации при введении в регрессию второй объясняющей переменной.

Решение. Значения коэффициентов детерминации для регрессий с одной и с двумя объясняющими переменными соответственно равны: R² = 0,97 и R² = 0,96. Увеличения значения не произошло. Введение второй переменной не увеличило адекватность модели.

 

3. Теоретические вопросы.